Centre de gravité d'un système à trois corps

[Deoxyribonucleic]

Bonjour,

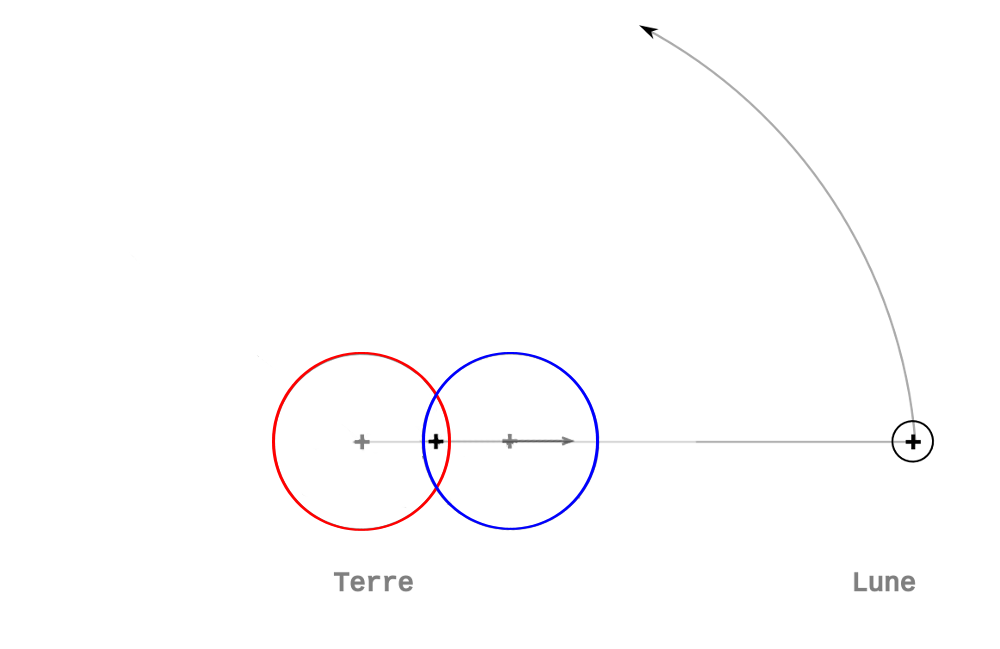
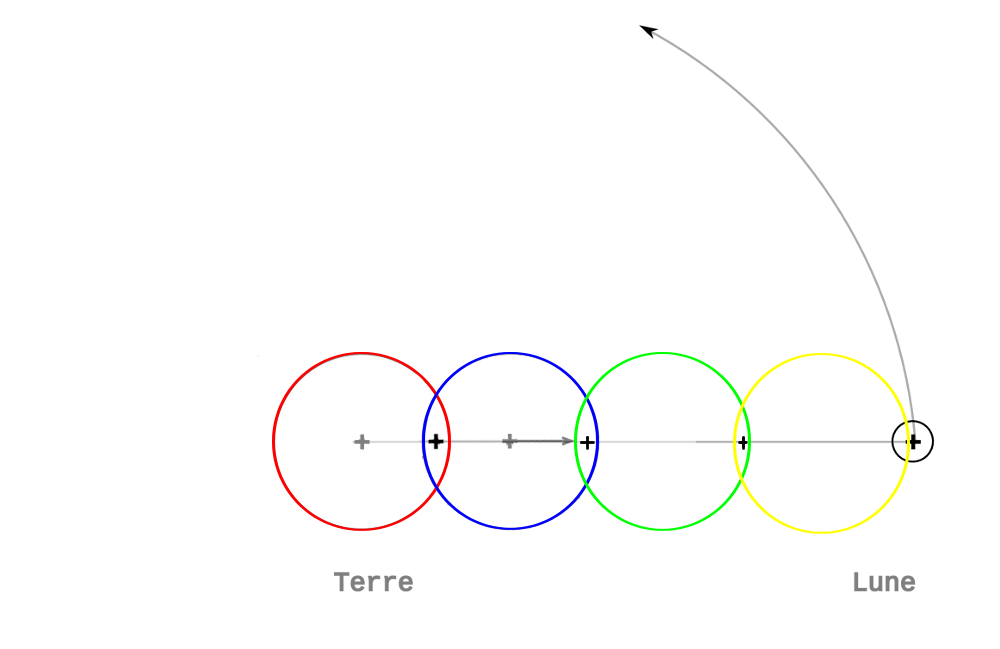
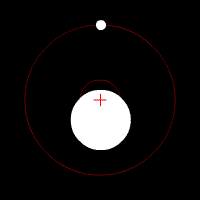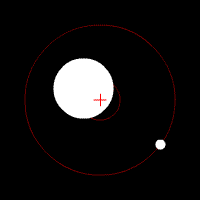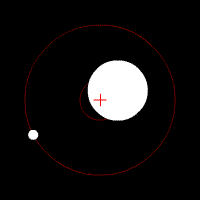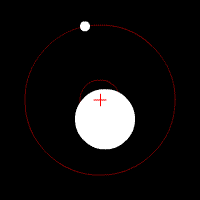
je viens ici pour vous soumettre une question : je me suis récemment demandé s'il existait un moyen de déterminer l'emplacement du barycentre dans le cadre d'un système avec trois corps de masses différentes mais chacune notable. En disposant des données de distances par exemple et de masses, trouver le centre de gravité.
J'ai, en faisant quelques recherches préliminaires trouvé des solutions mais je n'ai hélas pas le niveau pour comprendre certaines solutions et savoir si elles correspondent à ce que je voudrais savoir (le "problème à n corps" par exemple, sans savoir s'il est applicable ici, et que je ne comprends de toutes façons pas vraiment), ou alors des solutions "simplifiées" mais qui ne correspondent pas à ce que je veux faire (le "problème à n corps restreint" par exemple qui ne considère que deux corps en imaginant que le pouvoir attractif de l'autre est négligeable).

De plus, indépendamment de ma précédente question, j'aimerais également savoir s'il était possible de calculer les orbites de ces trois corps autour de ce barycentre.

Merci d'avance pour vos réponses et toutes mes excuses pour la question à un sujet certainement déjà traité, mais auquel je n'arrive pourtant pas à trouver une réponse claire et schématique, bien qu'il m’apparaisse pourtant comme "relativement simple" dans l'énoncé.
-----

[Gilgamesh]

En deux mots :

Trouver le barycentre est élémentaire.

Déterminer l'orbite est plus compliqué mais surtout donne un résultat sensible aux conditions initiales donc fondamentalement instable, au mieux métastable.

[Deoxyribonucleic]

Merci pour cette réponse rapide et concise.

Je suis du coup intéressé, si possible, par une formule ou un moyen, une ressource disponible sur internet ou autre de déterminer le barycentre dans les conditions que j'ai décrites.

[Gilgamesh]

Barycentre de trois points dans le plan ou dans l'espace

[A voir en vidéo sur Futura]

[Deoxyribonucleic]

Merci, mais bien entendu je connaissais cette méthode, ma seule question était comment l'appliquer dans le cas où les trois "points" du triangle étaient des corps célestes de masses différentes, puisque ce chapitre considère le système comme pondéré ? La réponse est certainement tout aussi simple mais c'est pourtant ça que je n'arrive pas à faire, et n'arrive pas à trouver la réponse sur la page wikipédia non plus.

[Deedee81]

Salut,

Merci, mais bien entendu je connaissais cette méthode, ma seule question était comment l'appliquer dans le cas où les trois "points" du triangle étaient des corps célestes de masses différentes, puisque ce chapitre considère le système comme pondéré ? La réponse est certainement tout aussi simple mais c'est pourtant ça que je n'arrive pas à faire, et n'arrive pas à trouver la réponse sur la page wikipédia non plus.

Je ne comprend pas trop bien où est la difficulté puisque pour trois corps célestes, si tu connais leur position et leur masse (*), il suffit d'appliquer la formule donnée dans wikipedia (avec les coefficients a, b, c pour les masses et les x_a, etc.... pour les vecteurs positions)

(*) maintenant si tu ne connais pas les positions ou les masses, c'est impossible de calculer le centre de gravité.

[Deoxyribonucleic]

Merci !
En fait ces même coefficients je les avais "zappé" dans mon esprit. J'étais passé dessus sans voir que ça correspondait à ce que je cherchais.

[Deoxyribonucleic]

Je reviens vous voir avec une question qui concerne toujours le centre de gravité mais est beaucoup plus théorique.. (mais certainement aussi naïve hélas).

Il y a en effet quelque-chose que je n'arrive toujours pas à saisir, si on cherche le barycentre de cette manière, sachant que les astres se déplacent et ne sont pas forcément en résonance, le barycentre que l'on va observer devrait aussi changer d'emplacement ?

Or ce n'est, je pense, heureusement pas le cas normalement (je précise que je parle bien d'un cas hypothétique où, pour simplifier, le barycentre de ce système n'est en orbite autour de rien du tout, et où aucunes forces telles que l'expansion de l'univers ou autre n'interviennent) ?

J'ai un peu de mal à formuler ma question et espère que vous arriverez tout de même à me comprendre. Ce que je veux dire c'est, avec ce système de calcul, le centre de gravité est donc censé se déplacer en fonction des orbites respectifs des corps célestes ? Si j'ai raison (j'ai peur d'avoir déjà faux dans mon raisonnement), peut-on calculer le barycentre "absolu" en fonction de chaque déplacement orbital possible des corps ? Quitte à admettre que ces corps décrivent des orbites parfaitement circulaires.

Encore une fois merci d'avance.

[Amanuensis]

Si les trois corps forment un système isolé (aucune influence externe au système), alors, en mécanique classique, le barycentre a un mouvement rectiligne uniforme dans un référentiel inertiel.

Ou encore, il existe un référentiel inertiel tel que le barycentre soit immobile.

Ou encore, si on prend un des trois corps comme référence, immobile, alors le barycentre aura un mouvement accéléré, une orbite "miroir" de celle du corps de référence. Cela peut se transformer de manière à obtenir un référentiel avec le barycentre immobile (plus qq autres contraintes), ce qui est une manière de construire le référentiel inertiel le plus adapté à traiter le problème.

[Dynamix]

Salut

Le centre de masse d' un système isolé a une vitesse constante .
Un référentiel accroché à ce point est donc galiléen .

Zut !
Grillé !

[Deoxyribonucleic]

Merci pour votre réponse à tous les deux, je comprends un peu mieux, c'est une question de point de vue et selon un point de vue inertiel classique on peut observer un mouvement régulier et constant.

[Deoxyribonucleic]

Rebonjour,

il me reste encore une dernière question très en lien avec la précédente, c'est pourquoi je ne reposte pas de sujet :

Voilà je me posais une autre question certainement très basique également (il faut vraiment que je me procure un ouvrage sur ça) :

Dans le cas du système Terre-Lune, le centre de gravité du système T-L est distinct du centre de gravité de la Terre. Cependant d'après ce que j'ai compris grâce à l'action des forces de marées terrestres, à l'usage, la lune a peu à peu ralenti et s'est "liée" (résonance spin-orbite).
Toujours est-il qu'à la base cette résonance ne jouait pas, ce qui signifie possiblement qu'une disposition Terre-Lune comme vue ci dessous (Terre dans sa position bleue ), ce qui signifie que dans ce cas le barycentre du système devait changer pour se retrouver toujours entre la Lune et la Terre ?



Vu qu'on m'a précisé que selon le référentiel galiléen le barycentre, si j'ai bien compris, lui même référentiel galiléen, n'effectuait par définition qu'un mouvement de translation rectiligne, et sachant qu'il n'est pas possible, sinon cela créé un paradoxe, que le barycentre dépendent de l'orbite de la terre et que l'orbite de la terre dépende du barycentre... Quelle force, principe ou loi que j'ai négligée dans ma réflexion (c'est un bien grand mot) fait que la situation que j'ai montré plus haut (Terre bleue et lune, toujours) est (était) impossible ?

[Amanuensis]

Toujours est-il qu'à la base cette résonance ne jouait pas, ce qui signifie possiblement qu'une disposition Terre-Lune comme vue ci dessous (Terre dans sa position bleue ), ce qui signifie que dans ce cas le barycentre du système devait changer pour se retrouver toujours entre la Lune et la Terre ?

La figure n'est pas encore visible, et donc je vais peut-être répondre à côté, faute d'avoir bien compris la question.

À cause des marées, la Lune et la Terre s'éloignent l'une de l'autre. Cela implique qu'on a aussi bien un éloignement entre la Terre et le barycentre que entre la Lune et le barycentre. Faut penser le barycentre "immobile", avec la Lune et la Terre s'en éloignant chacune de son côté (la Lune s'éloignant plus vite que la Terre, dans le rapport inverse des masses).

(Précisons aussi que quand on dit que la Terre parcourt une ellipse autour du Soleil, c'est une approximation négligeant la Lune. Il serait plus précis de dire que c'est le barycentre Terre-Lune qui a une orbite elliptique, la Lune comme la Terre ayant un mouvement supplémentaire autour de ce barycentre.)

[Deoxyribonucleic]

Étonnant que la figure ne soit pas visible ?

Ce que j'ai dû mal à comprendre avec cet "éloignement de la Lune et de la Terre chacune de leur côté" (bien que ton message m'est aidé à y voir plus un peu clair) c'est la façon par laquelle se matérialise cet éloignement de manière schématique ? Que le centre de gravité terrestre se rapproche peu à peu du barycentre du système T-L, ce qui est corrélé avec l'influence décadente de la gravité lunaire sur celui-ci étant donné que la lune s'en éloigne ? On a donc un agrandissement de l'orbite lunaire et un rapprochement du centre de gravité terrestre avec le barycentre actuel ? Est-ce exact ?

[Dynamix]

On a donc un agrandissement de l'orbite lunaire et un rapprochement du centre de gravité terrestre avec le barycentre actuel ? Est-ce exact ?

Non pas du tout .
Si la lune s' éloigne du barycentre , la terre s' en éloigne aussi sinon ce ne serait plus le barycentre .
Sur ton dessin on devrait voir 2 barycentres :
Un pour terre bleue + lune
Un pour terre rouge + lune

[Deoxyribonucleic]

Mais du coup, vu que la terre orbite autour de ce barycentre, cela induirait un rapprochement de la lune non ? (sachant qu'on a changé de référentiel et que désormais celui ci est la lune).


(je ne suis pas sponsorisé par les Jeux Olympiques)

Je sais que j'ai faux mais je n'arrive toujours pas à comprendre pourquoi..

[Dynamix]

(sachant qu'on a changé de référentiel et que désormais celui ci est la lune).

Le référentiel lune n' est pas galiléen .
Le référentiel terre non plus .

[Deoxyribonucleic]

Je sais, mais c'est visiblement le référentiel de mon schéma (bon, qui est faux à la base) dans tous les cas.

Ce que je n'arrive pas à comprendre en fait c'est comment la Terre peut tourner autour du barycentre, si celui s'ajuste dès que la Terre se rapproche ou s'éloigne de la Lune, cela signifie qu'à chaque apogée ou périgée (et entre les deux) le barycentre se déplace (selon le référentiel terrestre, ou lunaire).. Mais sachant que la Terre orbite autour de se barycentre si celui-ci se déplace (ce qui n'est pas le cas dans la réalité, du moins pas de cette façon, il se déplace de manière rectiligne) la Terre continue de se déplacer et etc..

Ma vision des choses est certainement fausse et c'est tout l'objet de ma question, je ne comprends pas pourquoi. (du coup merci à vous de tenter de m'aider.. Je formule sûrement très mal mon interrogation...)

[Dynamix]

je ne comprends pas pourquoi

Parce que tu ne raisonne pas dans le bon référentiel .

[Deoxyribonucleic]

Tu dois avoir raison. Mais j'ai toujours du mal à comprendre..

[Deoxyribonucleic]

Bon du coup j'ai finalement compris grâce à cette image :

Source

La Lune est opposée à la Terre par rapport au barycentre quoiqu'il arrive (ce qui est logique en fait).

Tu avais totalement raison en fait, erreur de référentiel, je voulais absolument faire effectuer un mouvement à ce barycentre je ne sais pas pourquoi...

[Amanuensis]

je voulais absolument faire effectuer un mouvement à ce barycentre je ne sais pas pourquoi...

Parce que c'est normal. Dans un référentiel où le Soleil est fixe, ce barycentre a un mouvement: une orbite autour du Soleil.

Il n'y a pas de "bon référentiel" dans l'absolu, il n'y a que des choix de référentiel adaptés à telle ou telle question.

Si la question porte sur les mouvements de la Terre et de la Lune "autour" de leur barycentre commun, alors le meilleur choix est de prendre un référentiel tel que ce barycentre est immobile.

De même que pour servir un café dans un avion en croisière, le plus simple pour le steward est de penser dans un référentiel où l'avion est immobile!

---

Notons aussi que le barycentre se déplace par rapport à la Terre, quand la rotation de celle-ci est prise en compte: si on cherche les latitudes/longitudes de ce barycentre, elles varient dans le temps (pour rester face à la Lune).

Bref, l'idée de mouvement est inséparable du choix de référentiel.

[Dynamix]

Bref, l'idée de mouvement est inséparable du choix de référentiel.

Il faut chercher le plus simple si on ne veux pas s' emmêler les crayons .

[Mailou75]

un ptit lien qui peut t'interesser
http://forums.futura-sciences.com/as...ml#post4129784

[Deoxyribonucleic]

Je retiendrai à l'avenir pour le référentiel, encore merci

Pour le lien je viens de le survoler et les schémas sont sympas, je ne me suis pas trop attardé sur les calculs je dois t'avouer... Et je n'ai pas tout compris pour les trois derniers messages...

[Mailou75]

C'était juste pour les schémas, montrer qu'il existe des référentiels où le centre de gravité G est en mouvement