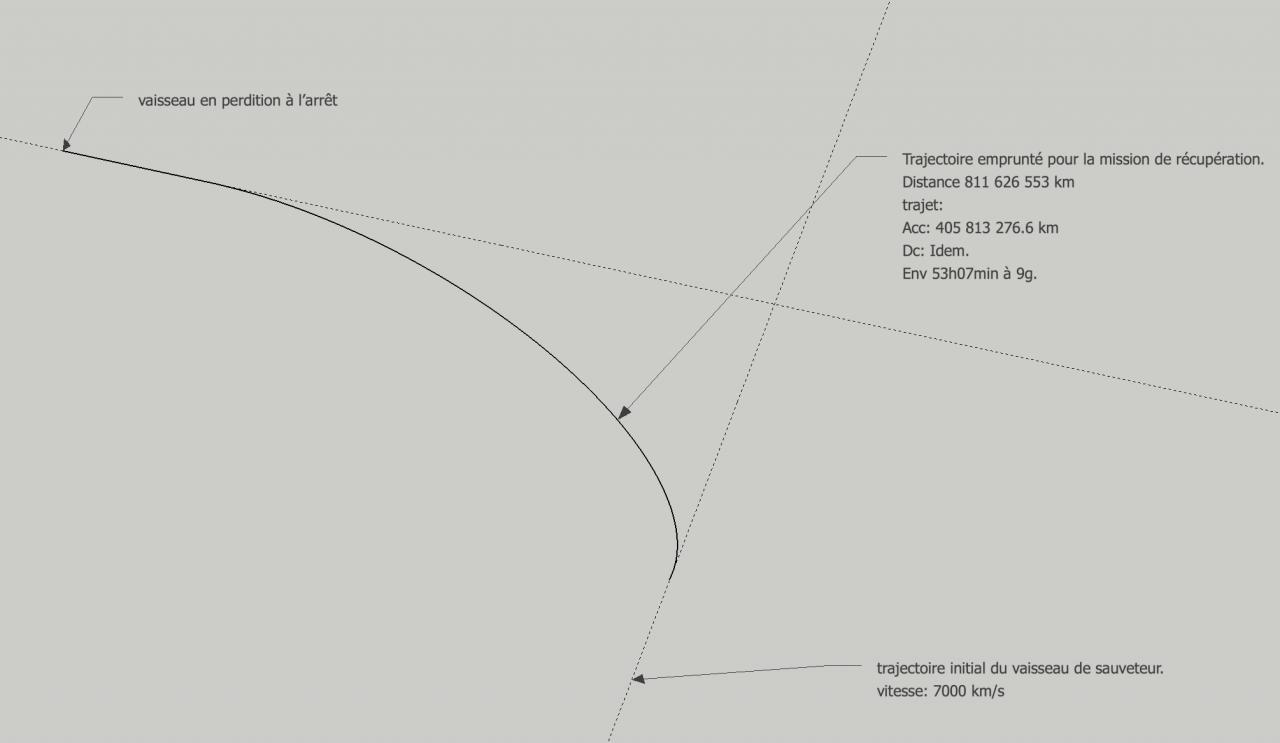
Bonjour,
Une sphère en rotation de 1km de rayon a une vélocité angulaire de 0.9456 tpm (soit env 356 km/h) et une vélocité linéaire d'env 356 km/h, produisant une poussée de 1g.
J'aimerais savoir si, dans l'espace (sans tenir compte des forces environnantes) un objet munie de deux propulseurs induirait ce mouvement circulaire et ainsi reproduire un cercle parfait?
Je suppose que oui...
Je constate aussi que les deux vélocités sont identiques (je passe outre la phase d'accélération), est-ce à dire qu'avec une puissance différente pour chaque moteur l'on pourrait reproduire un circuit elliptique?
Si c'est le cas doit t'il y avoir un moteur en accélération et l'autre à vitesse constante ou bien des accélérations différentes l'une à 1g l'autre 2 à 3g?
Merci.
-----




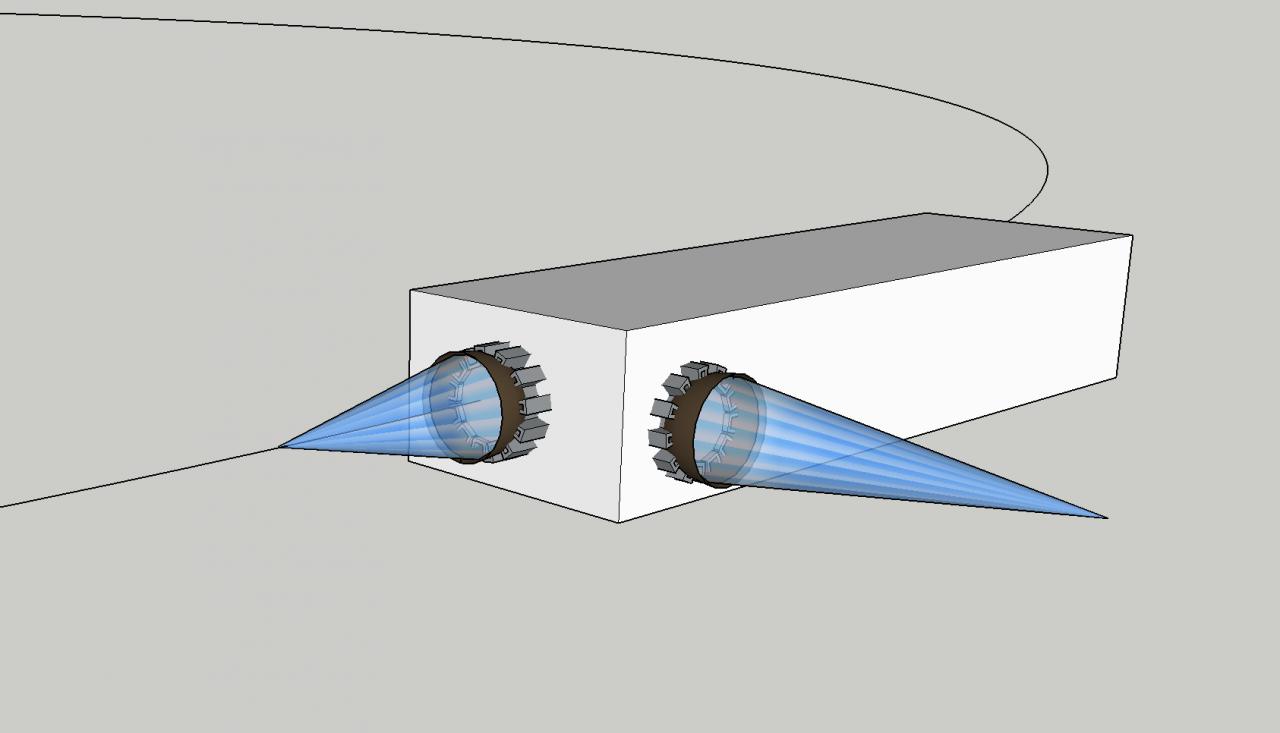
 existerait-il de la pesanteur mobile ? explication svp, merci.
existerait-il de la pesanteur mobile ? explication svp, merci.