Il ne devrait pas s'arrêter avant d'arriver en L2, il sera poussé lentement sur cette position d'arrêt puis mis en rotation.Envoyé par tezcatlipoca
Pas besoin de calculer puisque l'on doit l'augmenter progressivement, toujours avec l'impératif de ne pas dépasser celle qui ferait franchir le point d'équilibre en L2.
Je suppose qu'il y a une petite marche d'erreur acceptable pour sa position, ce n'est pas au mètre près ?
Faire tout pour la paix afin que demain soit meilleur pour tous
https://fr.wikipedia.org/wiki/Orbite_de_Lissajous
Voir aussi à Liapounov. On n'est pas dans l'intuitif.
Si, si.
Quand le téléscope monte, tout le système solaire se retrouve en-dessous de lui, donc, la gravité le fait redescendre. Et quand il passe au-dessous, la gravité du système solaire le fait remonter.
Quand il retarde derrière la Terre, il est attiré par cette dernière et accélère. Quand il repasse devant, la Terre, derrière lui, le ralentit.
Dans un champ de gravitation uniforme (quand on lance un caillou), la vitesse décroît linéairement par rapport au temps. Elle devient nulle, puis négative : le caillou retombe.
Pour le téléscope, c'est plus compliqué. Comme il s'éloigne de la Terre, il n'est pas dans un champ de gravitation uniforme. Au fur et à mesure qu'il avance, la force d'attraction de la Terre qui le ralentit est de plus en plus faible. Elle décroît en 1/r2 avec la distance au centre de la Terre.
Donc sa vitesse ne décroît pas linéairement.
Dans un espace vectoriel discret, les boules fermées sont ouvertes.
Vu
Ou plutôt merci beaucoup.
T'as raison, pas du tout dans l'intuitif.
Pio2001 nous avait déjà livré des éléments permettant d'éclaircir la question (sur la page précédente).
Merci à lui.
Comme tous les satellites placés en orbite autour de L2, le JWST embarque une réserve d'ergols pour pouvoir maintenir sa trajectoire. Il me semble avoir lu qu'il fallait des corrections toutes les trois semaines environ.
Bonsoir.
Le point de Lagrance est en fait une orbite autour du soleil, c'est un point "fixe" par rapport à l'ensemble soleil/terre, on devrait dire par rapport aux centres de gravité de la terre et du soleil.
Je trouve ça ici, c'est moi qui souligne.
e long de la ligne Soleil-Terre la gravité est la conjugaison de deux effets: celui du Soleil, une sphère, laquelle peut être réduite en un point (c'est la masse qui importe, pas le volume); on retrouve la même chose pour la Terre (elle aussi est une sphère). En étant placé sur la ligne Soleil-Terre, la gravité exercée est équivalente à la somme des masses placées au centre de gravité de l'ensemble (barycentre).
Avec ce système, réduit en une sorte de "ligne" en rotation, il existe un point sur la ligne, et de chaque côté du centre, qui peut tourner en synchronisme, à condition de se trouver sur l'orbite stationnaire: ni trop près du centre pour ne pas être attiré et plonger; ni trop loin auquel cas il s'échapperait. Tout se passe comme si, un satellite en ce point était en orbite autour du centre de masse.
Dans les villages gaulois, ils ne sont jamais tous d'accord. Jules César
A noter que cette orbite est stable dans les deux directions perpendiculaires à l'axe Soleil - Terre. Si on s'en éloigne, on y est à nouveau attirés.
Mais instable dans la direction Soleil - Terre. On est comme sur la pointe d'une aiguille. Si on bascule d'un côté, il faut donner un coup de propulseur pour revenir à l'équilibre.
Si à la fin on s'en éloigne, en toute logique, on devrait se retrouver sur une orbite elliptique autour du Soleil, qui croise celle de la Terre.
Je me demande si le téléscope pourrait rester sur cette orbite en présentant toujours la même face au Soleil (la face avec le bouclier thermique, tant qu'à faire).
Dans un espace vectoriel discret, les boules fermées sont ouvertes.
https://blogs.nasa.gov/webb/
Traduction corrigée :
Le miroir primaire de Webb prend sa forme définitive. Aujourd'hui, le premier des deux panneaux latéraux, a été déployé et verrouillé avec succès. Chaque panneau latéral contient trois segments du miroir principal. Ils ont été conçus pour se replier afin de réduire le profil global de Webb pour le lancement et le trajet vers L2.
Le processus de déploiement de l'aile bâbord a commencé vers 8 h 36 HNE. Vers 2 : 23 heures HNE, les ingénieurs ont confirmé que le panneau était entièrement sécurisé et verrouillé en place son déploiement était achevé.
https://www.jwst.nasa.gov/content/we...30fps_h264.mp4
Maintenant que le panneau d'aile bâbord est verrouillé en place, les équipes au sol se préparent à déployer et verrouiller le panneau tribord (côté droit) demain. Au terme de ces opérations, le Webb aura terminé sa séquence de déploiement majeur.
Merci bien à tous les posteurs qui ont essayé d'éclairer ma lanterne.
Je dois dire que les 2 dernières explications données m'ont permis de comprendre un peu mieux.
C'est dommage que je n'ai pas trouvé cette orbite de lissajoux avec les forces qui s'excercent en fonction de la position de JSW sur l'orbite ( et surtout à quoi elles sont dûes)
C'est vrai que pour moi ce n'était pas vraiment intuitif et ce fut une surprise de savoir que ce point fictif de Lagrange pouvait se comporter comme "un centre de masse" permettant que créer une attraction et donc une orbite stable autour de lui.
Non! Non!
Je pense que tu n'as pas très bien saisi.
Ce point fictif ne crée aucune attraction.
Mais je laisse poursuivre le(s) spécialiste(s)...
Dans deux des trois directions de l'espace, il est attractif.
Dans la troisième, il est répulsif.
Dans un espace vectoriel discret, les boules fermées sont ouvertes.
Je le répète, je ne suis pas physicien, donc...
Je continue de penser que cela est mal exprimé et que nous ne pouvons parfaitement dire ces choses qu'en langage physico- mathématique.
Si je devais m'avancer en vulgarisation, j'oserai dire que c'est un point d'équilibre entre des forces générées par le Soleil et le couple Terre-Lune (c'est ce que j'avais cru comprendre de tes premières explications).
Un point fictif, à mon sens ne peut crée aucune force d'attraction.
Il est fictif, sans masse.
De plus, pour ce que j'en sais il aurait du mal à être attractif dans deux directions et répulsif dans une autre, même si on pourrait avoir cette impression.
Nous ne sommes pas en électro-magnétisme mais parlons de forces gravitationnelles.
Bon, j'ai peut-être dit assez de bêtises.
Dites-moi si je dois retourner à l'école primaire ou secondaire...comme les miroirs.
Dernière modification par tezcatlipoca ; 08/01/2022 à 08h07.
Salut,
Un corps situé en L2 orbite autour du Soleil à la même vitesse angulaire que la Terre, alors qu'un corps en orbite à la même distance du Soleil en l'absence de Terre aurait une vitesse angulaire plus faible, puisque la vitesse angulaire d'un corps en orbite circulaire de rayon R autour d'une masse centrale M est (GM/R3)1/2.
Le corps situé en L2 est donc soumis à une accélération centrifuge supérieure à celle qui compenserait exactement l'accélération gravitationnelle qu'il subit de la part du Soleil, et devrait donc s'éloigner. Mais à cette dernière il faut ajouter l'accélération gravitationnelle qu'il subit de la part de la Terre, dans la même direction.
Après, c'est du bête calcul...
PS : pas trop mal expliqué dans la page wikipedia.
Dernière modification par yves95210 ; 08/01/2022 à 09h12.
message annulé
Dernière modification par yves95210 ; 08/01/2022 à 09h23.
Je te remercie Yves.
Bonjour,
ensuite si vous voulez en savoir plus sur la détermination d'une orbite de Lyapunov, vous pouvez vous attaquer à ce travail d'étudiants : https://scholar.google.com/citations...J:u-x6o8ySG0sC
On comprend bien la complexité de réaliser une orbite autour du point L2.
Dernière modification par Lansberg ; 08/01/2022 à 10h16.
Je capte quelques bribes dans l'intro, mais honnêtement, je suis vite largué.
Cela n'en reste pas moins intéressant pour un publique averti.
Bonjour à tous,
Le télescope sera à 1,5 millions de kilomètres de la terre et donc plus éloigné du soleil.
https://www.futura-sciences.com/scie...e-espace-8624/
La terre tourne autour du soleil en 1 an à la vitesse de 29,78 km/seconde (107.000 km/h).
Donc le JWST étant plus éloigné du soleil, il doit se déplacer plus rapidement autour du soleil afin de rester aligné et à la même distance avec la terre.
Comment a-t-il pu atteindre cette vitesse de ?? supérieure à 29,78 km/Sec ?
Je me souviens qu'au lancement d'Ariane que sa vitesse maximum a été proche de 10 km/Sec et puis cette vitesse s'est réduite progressivement.
J'ai ma réponse, il était déjà à la vitesse de la terre lors de son lancement, pas bien éveillé ce matin
Dernière modification par trebor ; 08/01/2022 à 12h04.
Faire tout pour la paix afin que demain soit meilleur pour tous
Mais en poursuivant le raisonnement à partir de l'explication que j'avais donnée, on peut au moins comprendre pourquoi l'équilibre en L2 est instable suivant l'axe Soleil-Terre-L2 :Je capte quelques bribes dans l'intro, mais honnêtement, je suis vite largué.
Cela n'en reste pas moins intéressant pour un publique averti.
Pour qu'un corps puisse rester stable sur l'axe Soleil-Terre un peu au-delà de L2 disons à une distance R+dR du Soleil, où R est le rayon de l'orbite suivie par L2, il faut qu'il ait la même vitesse angulaire ω autour du Soleil que L2 (et la Terre).
Etant plus éloigné du Soleil et de la Terre, l'accélération gravitationnelle qu'il subirait est plus faible qu'en L2. Au contraire, son accélération centrifuge serait plus forte qu'en L2, selon le même raisonnement que ci-dessus, puisqu'elle vaudrait (R+dR)ω au lieu de Rω.
Inversement, bien sûr, un corps restant stable sur l'axe Soleil-Terre un peu en-deçà de L2, subirait une l'accélération gravitationnelle plus forte qu'en L2, alors que son accélération centrifuge serait plus faible.
Donc dans les deux cas pour que le corps reste stable il faudrait lui fournir une accélération permanente en direction de L2. Et un corps situé exactement en L2 et ne disposant pas d'un moyen de propulsion serait en équilibre instable, une simple pichenette suffisant à l'éjecter soit vers l'extérieur du système solaire soit vers l'intérieur.
Pour ma part les calculs sont désormais au dessus de mon niveau, cela fait longtemps que je n'ai plus le niveau que j'avais en à la fin de mon DEUG AJe capte quelques bribes dans l'intro, mais honnêtement, je suis vite largué.
Cela n'en reste pas moins intéressant pour un publique averti.
Mais j'ai retenu ceci.
" De ces orbites périodiques autour des points de Lagrange sont issues des variétés invariantes (tubes de Conley-McGee) qui sont des séparatrices de la dynamique[Quoi ?] et qui en ce sens peuvent être considérées comme des courants gravitationnels. De plus en plus, ces courants sont utilisés pour la conception de missions, notamment le réseau de transport interplanétaire (ITN)6."
Même si je n'en comprend pas vraiment la raison, le résultat est que ce point de Lagrange agit bien comme un courant gravitationnel.
Tout cela me semble très cohérent. Merci encore à Yves.
Dernière modification par tezcatlipoca ; 08/01/2022 à 12h25.
A mon sens aussi, mais ce n'est pas ce que semble dire cette partie de WIKI
" De ces orbites périodiques autour des points de Lagrange sont issues des variétés invariantes (tubes de Conley-McGee) qui sont des séparatrices de la dynamique[Quoi ?] et qui en ce sens peuvent être considérées comme des courants gravitationnels. De plus en plus, ces courants sont utilisés pour la conception de missions, notamment le réseau de transport interplanétaire "
Là non plus je n'ai pas vraiment compris ce que voulait dire Pio2001
Bonjour Yves.
Ce n'est pas avec cette partie là que j'ai un problème, tant que l'on reste sur l'axe Soleil Terre L2 je comprends bien la necessité de fournir une accélération minime pointant vers L2 pour y revenir quelque soit le sens où l'on s'en écarte. Accélération d'autant moins forte si l'on réagit rapidement dès qu'on s'éloigne du point d'équibre.
C'est lorsque l'on est sur l'orbite de Lissajous donc si j'ai bien compris grosso modo dans un plan à peut près perpendiculaire à l'axe Soleil Terre L2.
Quelle force permet JWST d'être " attirée vers le point de Lagrange 2" et rester sur cette orbite.
Mais bon je reconnais que mes capacités sont vieillissantes, c'est pour cela que je me suis contenté de l'affirmation WIKI donnée plus haut mais sans en comprendre la raison.
Dans un repère tournant autour du Soleil avec la Terre, dont l'axe x est l'axe Soleil-Terre, l'axe y dans le plan de l'écliptique et orthogonal à l'axe x (comme la tangente à l'orbite de L2) et l'axe z orthogonal au deux autres (donc au plan de l'écliptique), l'explication que j'ai donnée ci-dessus montre que L2 est "répulsif" suivant l'axe x puisque dès qu'on s'éloigne de L2 dans un sens ou dans l'autre suivant l'axe x, l'accélération totale (gravitationnelle + centrifuge) est dirigée à l'opposé de L2.
Mais, comme Pio l'a expliqué, il est "attractif" suivant les deux autres axes, puisque seules entrent en compte les accélérations gravitationnelles causées par le Soleil et par la Terre, dont les composantes en y et en z tendent à rapprocher le corps de l'axe x.
Dans ce repère, un corps en orbite autour de L2 a une accélération centrifuge supérieure à celle de L2 dans la moitié de l'orbite où la projection de la vitesse du corps sur l'axe y a le même sens que la vitesse de L2, et une accélération centrifuge inférieure à celle de L2 dans l'autre moitié de l'orbite (il faut bien sûr que le plan de cette orbite soit différent du plan défini par les axes x et z).
Intuitivement on voit donc que, à condition de bien calculer son coup, on peut arriver à compenser (sur une période orbitale) l'effet répulsif de L2 suivant l'axe x, dû pour x > x(L2) à l'excès d'accélération centrifuge et pour x < x(L2) au déficit d'accélération centrifuge qu'aurait un corps statique dans ce repère. Pour cela, si je ne dis pas de bêtises (je n'ai pas regardé les calculs), il faut "simplement" que dans la première moitié de l'orbite (celle où il y a un excédent d'accélération centrifuge), x soit < x(L2), et dans l'autre moitié x > x(L2).
D'où l'allure de ces orbites, dont le plan est incliné par rapport à celui orthogonal à l'axe x :
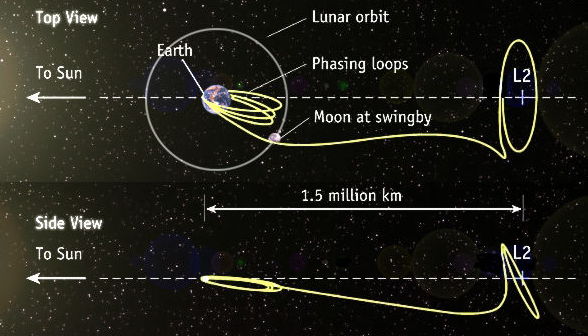
PS : croisement avec le message d'arbanais; mais j'espère que ça répond (sans calculs...) à sa question.
Dernière modification par yves95210 ; 08/01/2022 à 13h28.
Salut Arban',
Désormais, je m'en tiens aux explications d'Yves et des sources qu'il nous a proposé.
J'ai au moins l'impression d'avoir compris l'essentiel mais il faut que je m'accroche n'étant pas familier en ce domaine.
Merci à Yves et aux autres pour leur patience.
Avec les dernières explications d'Yves cela prend forme même s'il faut que je m'y reprenne à plusieurs fois, je sens le bon bout.
Moi non plus ! Mon bac+2 en math-physique date d'il y a 45 ans, je n'ai plus fait de physique durant le reste de mes études et n'ai jamais utilisé mes connaissances en physique professionnellement. Autant dire que j'avais quasiment tout oublié (il y a d'ailleurs certains domaines dans lesquels je suis totalement ignare aujourd'hui bien que les ayant étudiés à l'époque).
Je me rappelais quand-même avoir entendu parler des points de Lagrange en cours, ainsi que de leur (in)stabilité, même si je suis à peu près sûr qu'on n'avait pas étudié la question d'une orbite autour d'un des points instables. Mais heureusement il y a wikipedia (ou autres ressources sur le web)...
Avec ma licence d'histoire et Géo d'il y a aussi 45 ans, je me sens un peu comme Arbanais, fragile sur mes bases.
Mais je dois avouer que la clarté de tes explications m'ont été d'un grand secours.
