Bonjour à tous,
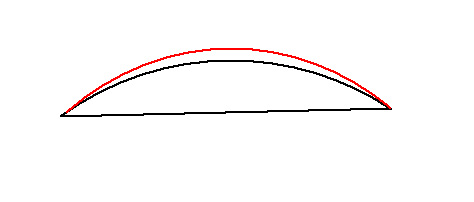
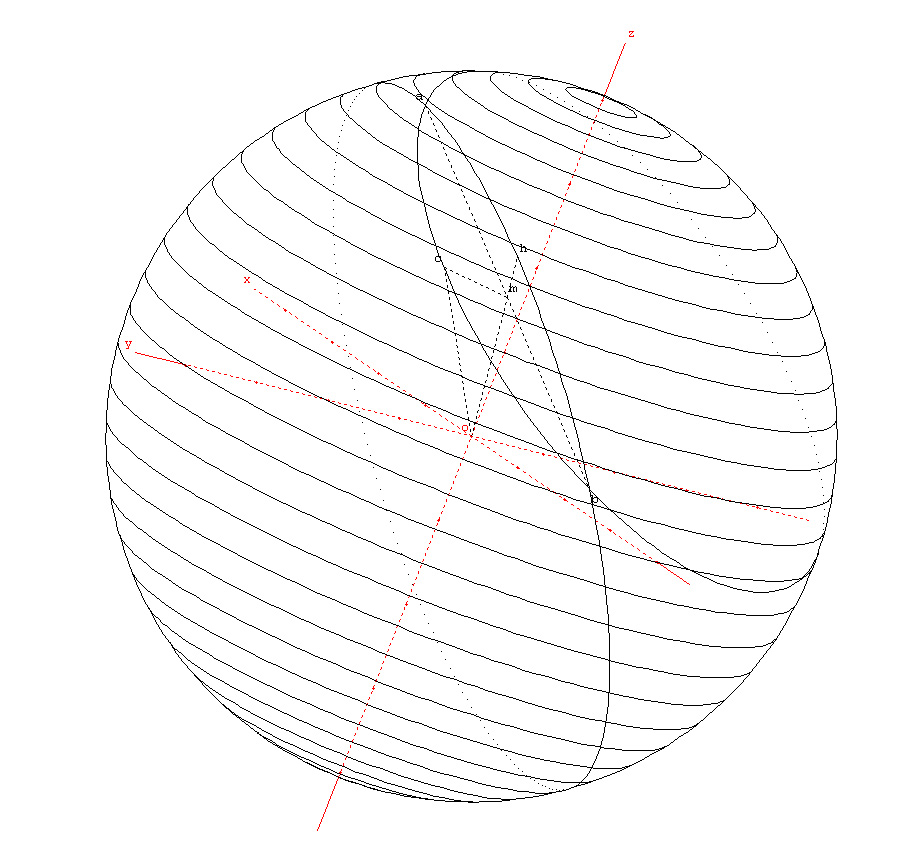
Voilà est ce que une âme charitable pourrait m’expliquer pourquoi une Orthodromie est plus courte qu'une loxodromie .
J'ai beau faire des recherches je n'arrives pas à comprendre avec les démonstrations (je suis en terminal donc c'est encore un peu complexe pour moi ) .
Il y a juste les illustrations de wikipédia qui me permettent de comprendre un peu sans plus ...
Merci.
Si tu cherche une démonstration mathématique convaincante, il faut toi même faire le ratio des deux trajets et trouver qu'il est forcément supérieur à 1 en mettant le loxodromique au numérateur.
Si c'est plus un aperception intuitive que tu cherches tu peux imaginer faire tourner un caillou au bout d'un fronde. Le trajet du cailloux est forcément orthodromique (la ficelle tendue représentant le rayon de la trajectoire, passant vers un centre commun à tous les points) et tu te représente facilement que si le caillou se met à osciller sur une trajectoire équivallente à celle d'un navire parcourant son parrallèle sur une sphère terrestre, le chemin sera plus long.
Parcours Etranges
C'est plus un aperception intuitive que je recherchais .Si vous avez d'autre exemple autre que le caillou au bout d'un fronde je suis preneur .
Et si vous avez une explication avec les grand cercles de la sphère se serait super .
Un bel exemple qui montre que la loxodromie n'est la ligne droite sur la sphère :
http://www.mathcurve.com/courbes3d/l...xodromie.shtml
La loxodromie est une spirale de la sphère qui s'enroule autour des pôles.
Comprendre c'est être capable de faire.
Bonsoir, une petite idée pas aboutie : on prend la corde dans les 2 chemins, pour l'orthodromie, il s'agit d'une vraie portion de cercle au dessus de la corde, et il me semble que pour la loxodromie, ce n'est pas un cercle, certes, mais de plus l'arc passe au dessus de cette portion de cercle; , donc la distance est forcément plus grande , on a la même corde mais l'arc loxodromique passe au dessus ..La corde loxo serait plus profonde !
En rouge loxo, en noir ortho ...A démontrer !
Dernière modification par triall ; 01/10/2012 à 23h20.
1max2mov
Voila, je crois que je tiens l'idée : l'orthodromie est la façon de tracer le cercle de rayon le plus grand entre 2 points . Tous les autres chemins auront un rayon plus court (si on estime que ce sont des arcs de cercle) .Qui dit rayon plus court entre 2 points dit chemin plus long ! C'est presque ça, ce qui me gène , c'est l'allure du chemin loxodromique dans l'espace , ce n'est pas une portion de cercle . Par contre, il semble qu'entre A et B on peut tracer une portion de cercle qui fait le tour de la Terre , mais qui n'est pas ortho qui correspond au cercle de plus grand rayon! ...
1max2mov
Bonsoir, désolé si je monopolise, mais le problème m'inspire, je voulais poster une autre réponse avant d'aller se coucher ! .
Je crois avoir mieux . On prend 2 points quelconques A, B sur une sphère, le chemin ortho définit en fait un autre équateur .
Ainsi c'est tout comme si l'on voulait aller de A à B, 2 points placés sur l'équateur ! Il est évident que tout chemin qui ne suit pas exactement cet équateur(chemin loxo ou non!) est plus long ! Non ?
1max2mov
Tout d'abord je te remercie de tes réponses!
Puis,malheureusement pour toi je ne peux pas être d'une grande utilité car je suis moi même à la recherche de la "solution" .
.Bonsoir,je croyais que vous vouliez une perception intuitive, celle que je vous propose avec l'équateur me semble bonne. Vous prenez 2 villes situées exactement sur l'équateur , le plus court chemin est obtenu en suivant exactement cet équateur .Mais c'est bon, j'ai la démonstration
On prend donc 2 points sur la sphère, il n'existe qu'un plan qui passe par ces 2 points et le centre .Ce plan coupe la sphère en 1 cercle qui est l'équateur dont je parle .
Il suffit de montrer que tout écart de cet équateur augmente la distance parcourue :
L'équateur passe par ahb ; un autre chemin passe par acb , j'ai tracé la corde ab en pointillé ; je trace cm perpendiculaire à ab .
En considérant le triangle omc on a om+mc>oc ; or oc=r=om+mh ; on a ainsi mc>mh ...
Ainsi quelque soit m si le trajet dévie de l'équateur on retrouve le dessin du message 6 ; la courbe de l'orto passe au dessus , la distance de la courbe loxo (en rouge) est forcément plus grande .La surface donnée par la courbe rouge est plus grande, sa longueur aussi .(maths) .cela se démontre facilement avec les intégrales .
Application : exemple on doit rejoindre 2 ville situées exactement sur le 40 ème parallèle, et bien la route la + courte ne s'obtient pas en suivant ce 40ème; mais en passant au dessus avec la courbe ortho , pour laquelle le rayon est plus grand donc la distance plus courte sur la même corde ! Je suis à votre disposition si vous n'avez pas bien compris , mais j'espère que vous avez aussi saisi le côté intuitif, en fait , c'est ce que voulait dire Phys 4 avec sa fronde, je crois , mais je n'avais pas saisi non plus !
1max2mov
Effectivement,c'était bien une perception intuitive que je recherchais.
Votre dernier message m'a permis de visualiser tout ça .J'attend la validation de votre fichier pour pouvoir le voir.
Sinon je pense que j'ai cerné le problème.
Et je vous en remercie.
Pardon Il faut lire la courbe de loxo passe au dessus (rouge) voir dessin message 6 , vu que cm>mh quelque soit m et h..
Dernière modification par triall ; 02/10/2012 à 21h33.
1max2mov
