Le point sur les mesures non concordantes de la constante de Hubble

[ordage]

Bonjour
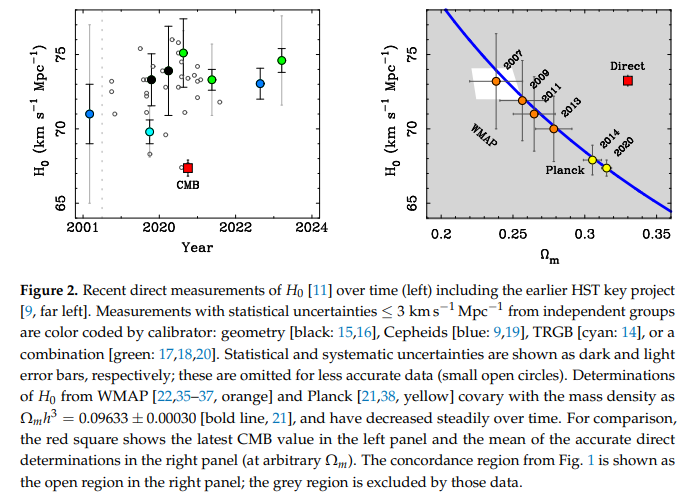
Les différentes méthodes (SN1A, Planck par analyse du CMB, lentilles gravitationnelles pour les quasars, ondes gravitationnelles, etc..) si elles donnent le même ordre de grandeur (à 10%) ont du mal à s'accorder sur une valeur plus précise. C'est à la fois inquiétant et intéressant. Déjà , on peut se demander jusqu'à quel point ces mesures sont indépendantes, et de plus ce que cette disparité de valeurs pourrait bien révéler sur les possibles biais des différentes méthodes et sur leur sensibilité à une modification de la théorie (que certains estiment mise en cause). Autrement dit y-a-t'il un truc qui nous échappe dans ces méthodes de mesure ou est-ce vraiment un défaut de la théorie actuelle. Existe-t-il des pistes dans des articles de synthèse qui traiteraient ce problème d'analyse comparative des méthodes de leur sensibilité aux paramètres, pour l'instant je n'ai vu que des conjectures.
Cordialement
-----

[yves95210]

Bonjour,

Je ne sais pas si tu as vu la discussion que j'avais ouverte ici il y a un an sans beaucoup de succès...
Le papier dont je parlais t'intéressera peut-être (je viens de voir qu'il a été mis à jour récemment et est publié dans l'édition du 01/12/2020 de The Astrophysical Journal Letters; je suppose donc qu'entre temps il a été peer-reviewed).

[ordage]

Bonjour,

Je ne sais pas si tu as vu la discussion que j'avais ouverte ici il y a un an sans beaucoup de succès...
Le papier dont je parlais t'intéressera peut-être (je viens de voir qu'il a été mis à jour récemment et est publié dans l'édition du 01/12/2020 de The Astrophysical Journal Letters; je suppose donc qu'entre temps il a été peer-reviewed).

Bonjour
Merci pour ta réponse.

J'ai lu ton post et téléchargé l'article (les auteurs ont fait un travail de romain). La méthode est intéressante et cela correspond à ce que je cherchais. Comme on peut s'en douter, il n'y a pas de conclusion à ce stade, mais des pistes. j'ai vu que les ondes gravitationnelles allaient aussi permettre une mesure, voir: https://www.ligo.org/science/Publica...ary-french.pdf. Je souhaite jeter un coup d’œil sur la cosmologie inhomogène, que je ne connais pas: un article à lire en premier, sur le sujet, à conseiller ?
Cordialement

[yves95210]

Je souhaite jeter un coup d’œil sur la cosmologie inhomogène, que je ne connais pas: un article à lire en premier, sur le sujet, à conseiller ?

Bonjour,

Peut-être déjà l'article wikipedia "Inhomogeneous_cosmology", qui contient pas mal de références.

Si tu es prêt à commencer par un peu de théorie (abordable, mais demandant de connaître les bases de la relativité générale), il faut lire la publication de Thomas Buchert:
On average properties of inhomogeneous fluids in general relativity.
Il y établit les équations sur lesquelles s'appuient ses travaux ultérieurs ainsi que, entre autres, ceux de David Wiltshire (son modèle de "Timescape cosmology", également cité dans le wiki).

Mais comme introduction tu peux lire cet article qui pose bien le débat, puisque débat il y a^(*), et qui contient d'autres références :
The Universe is inhomogeneous. Does it matter?

(*) Le débat ne porte pas sur la validité des équations de Buchert (qu'à ma connaissance personne ne conteste), mais sur l'importance de l'effet de "backreaction" qu'elles font apparaître lorsqu'on utilise les équations locales de la RG pour calculer les valeurs des scalaires moyens (expansion, densité de matière, courbure) sur un domaine spatial comobile, au lieu de se contenter de l'approximation de Friedmann et Lemaître consistant à considérer l'univers comme isotrope et homogène à toute échelle.

[A voir en vidéo sur Futura]

[ordage]

Bonjour
J'ai lu les références. L'article de Buchert, je l'ai survolé, un peu trop "hard" pour moi. J'ai vu qu'il utilisait le formalisme ADM , les congruences, les courbures extrinsèques et ce qui va avec .... Des souvenirs un peu lointains, en plus je n'ai jamais vraiment utilisé ce type de formalisme . En général c'est en vue d'une résolution numérique. Je n'ai pas vu dans son article si cela a été fait et avec quels paramètres (en particulier de rétroaction) cela produirait l'effet constaté de l'énergie noire.
La piste mérite, sans doute, d'être explorée.
Cordialement

[yves95210]

J'ai lu les références. L'article de Buchert, je l'ai survolé, un peu trop "hard" pour moi. J'ai vu qu'il utilisait le formalisme ADM , les congruences, les courbures extrinsèques et ce qui va avec .... Des souvenirs un peu lointains, en plus je n'ai jamais vraiment utilisé ce type de formalisme .

Perso, je me suis contenté d'admettre les équations issues du formalisme ADM que Buchert utilise dans la première partie du papier (section 2.1). La suite coule (presque) de source.
Depuis j'ai quand-même essayé de creuser, à partir du cours de Gourgoulhon (3+1 Formalism and Bases of Numerical Relativity). Mais pour moi aussi c'est trop hard...

En général c'est en vue d'une résolution numérique. Je n'ai pas vu dans son article si cela a été fait et avec quels paramètres (en particulier de rétroaction) cela produirait l'effet constaté de l'énergie noire.

L'article que j'ai cité en dernier mentionne que "the first papers to examine backreaction in numerical relativity have now begun to appear, (e.g., arXiv:1511.01105, arXiv:1511.05124)". Comme ça date de 2016, je suppose qu'il y a eu d'autres avancées depuis.

[pm42]

Pour ceux comme moi à qui il manque le temps et peut-être le courage de lire les articles cités et pour lesquels je te remercie, pourrais tu faire un très rapide résumé des pistes ?

[Sofaminou]

Pour ceux comme moi à qui il manque le temps et peut-être le courage de lire les articles cités et pour lesquels je te remercie, pourrais tu faire un très rapide résumé des pistes ?

Et de compréhension aussi non?
La question (et la section : Astrophysiciens, physiciens et étudiants avancés) étant précise, ouvrir un fil pour de l'annexe en discussion libre permettrait de garder le sujet premier, non?
D'ailleurs si un modo veut faire la manip et effeaer ces 2 derniers posts...

[Deedee81]

D'ailleurs si un modo veut faire la manip et effeaer ces 2 derniers posts...

Bonjour,

Excuse-moi, mais c'est la première intervention de pm42 dans ce fil. Qu'y a-t-il de mal à demander un résumé ? C'est souvent utile pour ceux qui veulent suivre la discussion.
(que quelqu'un ait le temps de le faire ou pas est un autre sujet)

[yves95210]

Pour ceux comme moi à qui il manque le temps et peut-être le courage de lire les articles cités et pour lesquels je te remercie, pourrais tu faire un très rapide résumé des pistes ?

Salut,

Les pistes permettant de résoudre le problème des mesures non concordantes de H₀ ?

J'avais déjà fait un résumé de l'étude citée dans l'autre discussion.

Si les auteurs de l'étude ont raison (je ne suis pas capable de le dire), ce n'est pas facile d'imaginer un modèle basé sur une "nouvelle physique" qui réponde à toutes les contraintes.

A moins de trouver des causes d'erreurs systématiques spécifiques à chacune des méthodes qui conduisent à une valeur de H₀ plutôt entre 72 et 75 km/s/Mpc à partir d'observations de l'univers récent (SNIa, lentilles gravitationnelles), il ne resterait comme pistes plausibles que celles qui expliquent cette non-concordance par une mauvaise prise en compte de la non-homogénéité de l'univers aux échelles inférieures à quelques centaines de Mpc,

- soit localement par le fait que nous (notre galaxie et l'amas auquel elle appartient) nous situons à l'intérieur d'une région de sous-densité. Cela constituerait un biais commun à toutes les méthodes mesurant H₀ à partir d'observations locales. C'est la piste évoquée par les auteurs de la publication citée. Mais le fait qu'une telle région suffise à expliquer un écart de plus de 1% entre la valeur de H₀ mesurée localement et celle calculée à partir des observations de Planck est difficilement compatible avec le modèle ΛCDM.

- soit de manière plus générale par le fait que l'univers s'écarte de plus en plus du modèle d'espace-temps spatialement homogène et isotrope de Friedmann-Lemaître à mesure que les grandes structures se forment. C'est l'idée des tenants des cosmologies inhomogènes, basées sur les équations de la relativité générale, mais se passant de l'hypothèse d'une densité de matière spatialement homogène à toute échelle.
C'est une hypothèse plutôt conservatrice puisqu'il ne s'agirait donc pas de "nouvelle physique", mais seulement d'appliquer correctement la RG dans un univers pas si homogène que ça. Pour résumer : à cause de la non-linéarité des équations de la RG, la valeur moyenne du taux d'expansion (à l'échelle à partir de laquelle on peut considérer l'univers récent comme homogène) calculée à partir des valeurs locales des paramètres de densité est différente de la valeur du taux d'expansion calculée selon le modèle de Friedmann-Lemaître à partir de valeurs spatialement constantes de ces paramètres.
La question est de savoir si les prédictions du modèle inhomogène s'écartent suffisamment de celles du modèle ΛCDM pour produire un effet observable (entre autres, si elles suffisent à expliquer l'accélération de l'expansion sans avoir besoin de faire appel à l'"énergie noire", on devrait aussi observer une courbure spatiale significative dans l'univers récent. La mission Euclid devrait permettre de confirmer ou de réfuter cette prédiction).

[pm42]

J'avais déjà fait un résumé de l'étude citée dans l'autre discussion.

En effet. J'avais attendu en vain que ton fil se développe pour le lire. Au temps pour moi.
Cette idée que nous serions dans une zone qui ne soit pas "moyenne" flotte depuis quelque temps en effet.

La mission Euclid devrait permettre de confirmer ou de réfuter cette prédiction

Ok et encore merci pour toutes ces infos et le résumé détaillé.

[Lugburz]

Bonjour,

Pourquoi les valeurs obtenues par WMAP et Planck sont elles incompatibles ?

Merci

[yves95210]

Pourquoi les valeurs obtenues par WMAP et Planck sont elles incompatibles ?

Elles ne le sont pas entre elles. Elles sont incompatibles avec les valeurs mesurées grâce à des observations de l'univers "local" (SNIa, etc.), puisque l'écart entre les valeurs déduites des observations du CMB et celles mesurées localement est proche de 10%, avec des barres d'erreur de l'ordre de +/- 1 à 2% pour les unes comme pour les autres et qui ne se recoupent donc pas.

[Lugburz]

Pourtant, lorsque je regarde les dernières valeurs données par WMAP (69,32 ± 0,8 km/s/Mpc) et Planck (67,4 ± 0,5 km/s/Mpc) elles ne se recouvrent pas. Il y a clairement un shift entre les valeurs de WMAP et Planck : https://fr.wikipedia.org/wiki/Constante_de_Hubble
On utilise pourtant la même méthode (CMB), pourquoi le changement d'instrument modifierai cette valeur ?

[yves95210]

Effectivement il y a un petit écart, même si pas comparable avec celui entre Planck et les mesures locales. Je savais que WMAP avait donné une estimation de Ho un peu supérieure à celle de Planck, mais je ne me rappelais pas que la marge d'erreur était aussi petite. Les premières estimations données par Planck, avec une marge d'erreur plus importante, étaient encore compatibles avec celles de WMAP.

Il faudrait regarder comment ont bougé les valeurs des paramètres cosmologiques qui sont mesurés directement (et à partir desquels Ho est calculé, puisqu'il ne s'agit pas d'une mesure directe), et si - pour ceux qui avaient déjà été mesurés par WMAP - les valeurs sont compatibles, ou si le modèle conduisant à ce calcul de Ho a été modifié : ce n'est qu'en combinant les résultats obtenus suivant plusieurs méthodes que Planck arrive à une estimation de Ho aussi précise. Si tu regardes le tableau page 16 de la publication des résultats de Planck 2018, tu verras que les estimations de Ho vont de 66.88 ± 0.92 à 69.9 ± 2.7 suivant les données utilisées...

Si tu as le courage (pas moi...) tu peux essayer de comparer les valeurs de tous les paramètres mesurés ou calculés par les deux missions (ici pour WMAP).

[physeb2]

Bonjour a tous,

pour compléter sur les différences entre PLANCK et WMAP j'aimerai ajouter ceci.

La différence de mesure entre WMAP et PLANCK peut venir de pas mal de choses. Il s’agit de l’observation du même « objet physique », le CMB, mais avec des instruments un peu différents et aussi avec des méthodes d’analyses légèrement différentes.

Les deux quantités d’intérêt sont la température et la polarisation linéaire des photons qui nous parviennent depuis toutes les directions possibles. Afin de mesurer avec grande précision ces deux quantités il est absolument nécessaire de caractériser toutes les contaminations possibles, en particulier ce qu’on appelle les avants plan (forqegrounds en anglais).

Le CMB est un rayonnement thermique (donc suit une loi de corps noir) qui aujourd’hui s’observe avec une température d’environ 2,725 K ce qui correspond majoritairement a des photons millimétrique et sub-millimétrique. Dans ces longueurs d’onde on retrouve pas mal de source astrophysique et en premier lieu la poussière de notre galaxie qui contamine l’observation sur de tres grandes échelles ainsi que des sources compactes comme certaines étoiles et des amas de galaxies (mais aussi notre propre planète, raison pour laquelle on envoie le plus loin possible notre satellite).

On peut voir a quoi ressemble les cartes d’observation de PLANCK dans les différentes fréquences d’observations ici:
https://www.cosmos.esa.int/documents...b-8b0ec55180db
Le système de coordonnées utilisé est le système galactique ce qui fait que la partie centrale des cartes est occupée par notre voie lactée. On peut voir que plus la fréquence est grande et plus la contamination est ample. Cependant il est nécessaire d’avoir le plus d’information possible dans des fréquences différentes afin de cross-valider la nature de la source comme c’est le cas de la détection de l’effet Sunyaev-Zeldovich des amas de galaxies sur le CMB.

Le nombre de fréquence pour PLANCK (30, 44, 70 Ghz pour LFI et 100, 143, 217, 353, 545 et 857 GHz) est plus important que pour WMAP (23, 33, 41, 61, et 94 GHz) et la précision est également plus grande. Tu peux voir que la contamination de la galaxie est franchement différente de pour les cartes de hautes fréquences qu’apporte PLANCK.

Ces différences font que les nécessités d'analyses furent différentes pour les deux satellites surtout pour les échelles angulaires plus petites. Pour analyser les cartes du lien précédent il est nécessaire de comprimer l'information se maniere statistique afin de pouvoir le comparer avec les modeles. Les perturbations de températures que l'on voit suivent plutôt bien un champs gaussaient aléatoire ce qui fait qu'on peut extraire la totalité de l'information (si en effet gaussien) avec la statistique de 2 points: Fonction de corrélation a 2 point en espace réel ou sa transforme de Fourier le spectre de puissance. Dans le cas du CMB il s'agit d'une sphère et donc l'approximation plane de l'analyse de Fourier a 2 dimensions n'est pas tres bonne et on utilise son équivalent sur une sphère a savoir la décomposition en harmonique sphérique, celle-la meme qui s'utilise en mécanique quantique pour décrire les électrons dans un atome. Cette décomposition dépend d'une échelle angulaire () et on appelle la statistique de 2 points le spectre de puissance angulaire . La maniere de passer des cartes a ce spectre de puissance utilise des méthodes complexes qui doivent tenir compte des avant-plans pour chaque fréquence. Lorsque le travail est finit on obtient les points suivants pour les perturbations avec un modele qui ajuste ces derniers:

CMB-power-spectrum-as-measured-by-WMAP-237-SPT-289-ACT-290-and-Planck-291-plot.png.jpeg

Dans ce cas le modele dépend typiquement de 7 paramètres dont fait parti. On peut voir que les points de WMAP s'arrêtent a quand ceux de PLANCK vont bien plus loin grâce au cartes de grandes fréquences. J'ai omis de dire que les grandes échelles angulaires correspondent aux petits , d'ailleurs la sphère entière, ce qu'on appelle le monopole, correspond a . Plus est grand et plus on regarde des taches de tailles plus petites. Notamment les échelles avec nécessitent qu'on nettoie les cartes des amas de galaxies pour être précis, chose que ne pouvait pas faire WMAP.

Pour finir, il existe plusieurs méthodes pour extraire le spectre de puissance pour les grandes et petites échelles pour la température mais aussi pour la polarisation. On obtient donc plusieurs jeux de données et PLANCK reporte donc plusieurs meilleurs ajustements qui correspondent a plusieurs valeurs de paramètres.

De plus, les données de PLANCK ne s'utilisent pas seules pour donner le résultat final. On utilise les résultats des autres expériences (en particulier venant de la mesure du pique des oscillations acoustiques des baryons dans la distribution des galaxies) ce qui pourrait également changer les valeurs en WMAP et PLANCK sur les valeurs de .

Je termine en précisant un point important sur la mesure de venant du CMB, elle dépend grandement de la mesure de la courbure de l'Univers. Cette courbure est liée a la position du premier pique que l'on voit dans le spectre de puissance et en admettant le modele cosmologique standard ainsi que l'apport d'autres mesures (comme la mesure de la baryogenese primordiale). Au final la mesure du taux d'expansion de l'Univers local dépend de ce que l'on admet de la courbure. On est plutôt confiant sur la mesure de cette courbure () et donc on peut prendre la valeur de pour ce cas particulier. On peut voir l'image suivante le résultat (probabilité postérieur) pour la densité de matière () et la courbure de l'Univers () en fonction de la valeur de . On voit que l'on obtient la valeur reporter pour ()

Capture d’écran 2021-03-03 à 22.24.02.jpg

[yves95210]

Salut,

Puisque cette discussion a été réveillée récemment, j'en profite pour mentionner une nouvelle mesure de H₀, utilisant une nouvelle méthode, qui donne elle aussi une valeur près de 10% supérieure à celle calculée à partir des observations de Planck et du modèle standard.

Cf. le blog "ça se passe là haut", et la publication en référence (je suppose qu'on peut la trouver sur arxiv).

[physeb2]

Bonjour yves95210,

c'est une méthode tres sympathique qui est en effet relié au sujet de cette discussion. Merci beaucoup pour l'ajouter ici.
Je vais aller regarder cet article car quelque chose m'interpelle. Si je me souviens bien de l'idée c'est que le nombre d'étoile dans un pixel de camera CCD augmente avec le carré de la distance et que le flux individuel observé pour ces étoiles diminue comme le carré de la distance. Donc la surface de brillance d'une galaxie ne varie pas avec la distance. En revanche la variance de flux mesuré entre les pixels, si on assume une distribution homogène des types d'étoiles dans la galaxie observée, va lui diminuer avec le nombre moyen d'étoile qu'il y a dans un pixel du CCD. Ainsi la fluctuation relative du flux des pixel diminue comme la distance. Ensuite on peut améliorer tout cela en passant dans l'espace de Fourier.

Cependant ici 3 choses m'ennuient quand on applique cette méthode pour des distances lointaines.
1- la diminution du "flux comme le carré de la distance" devient "le flux diminue comme le carré de la distance de luminosité" alors que le "la densité augmente avec le carré de la distance" devient "la densité augmente avec le carré de la distance angulaire". Ces deux distance ont un facteur entre les deux et ce n'est plus une constante...
2- quand on observe une galaxie lointaine la taille des pixels est assez grande en comparaison de l'image de la galaxie ce qui laisse peut de pixels sur lesquels évoluer la variance de flux, surtout si on doit assumer une évolution du profil de densité d'étoile de la galaxie avec le rayon.
3- En plus il faut prendre en compte qu'il y a une évolution du flux par effet de redshift pour le flux des étoiles observés dans une magnitude. Cela necesite de postuler un K-correction qu'on modélise avec les spectres des étoiles qui composent la galaxie. Cela necesite une estimation de la distribution d'âge des étoiles (qui dépend de la Star Formation History + redshift de la galaxie observé) et une fonction de masse initiale.

Pour ces raisons je ne pensais pas qu'on utiliserai un jour cette méthode pour la cosmologie.
Qu'en penses tu?

[yves95210]

Bonjour,

Selon un article prépublié tout récemment, l'écart entre les valeurs de H₀ estimées à l'aide du modèle standard à partir des observations de l'univers jeune (CMB, BAO, inverse distance ladder) et celles estimées indépendamment du modèle(*) à partir des observations de l'univers "local" (cosmic distance ladder) pourrait être dû à une mauvaise prise en compte de l'impact des inhomogénéités (très) locales sur la calibration de la magnitude des SNIa.

How does a smooth cosmic distance ladder emerge from observations made from a single location in a lumpy Universe? Distances to the Type Ia supernova (SN1A) in the Hubble flow are anchored on local distance measurements to sources that are very nearby. We described how this configuration could be built in a perturbed universe where lumpiness is described as small perturbations on top of a flat Friedmann-Lemaıtre Robertson-Walker (FLRW) spacetime. We show that there is a nonnegligible modification (about 11%) to the background FLRW area distance due to the presence of inhomogeneities in the immediate neighbourhood of an observer. We find that the modification is sourced by the electric part of the Weyl tensor indicating a tidal deformation of the local spacetime of the observer. We show in detail how it could impact the calibration of the SN1A absolute magnitude in the Hubble flow. We show that it resolves the SN1A absolute magnitude and Hubble tensions simultaneously without the need for early or late dark energy.

Je comprends à peu près la démarche mais suis totalement incapable de suivre les calculs...
Cela paraît en tout cas suffisamment sérieux pour que le cosmologiste Peter Coles en parle sur son blog.

(*) Remarque : ces estimations de H₀ ne sont pas si indépendantes du modèle que ça, puisqu'elles s'appuient sur un espace-temps FLRW même pour les petites valeurs de z (≤ 0,01) auxquelles se situent les échelons intermédiaires de la "cosmic distance ladder". Cette méthode n'est en fait indépendante que des paramètres du modèle (et donc de la loi d'évolution de H), mais elle suppose quand-même qu'il suffit de tenir compte du taux d'expansion d'un volume d'espace, sans se préoccuper de la manière dont ce volume peut se déformer aux échelles considérées.

Our target here is to explore in detail using the cosmological perturbation theory the assumption that the redshift is a monotonic function on all scales by calculating the monopole of the area distance on a constant redshift surface. This is very crucial because the local distance ladder is calibrated using distance measurement to nearby sources [9, 10]. It is well-known that distance to those sources is not a simple function redshift [16–18]. Several works have studied the luminosity distance (distance modulus) in perturbation theory before [19–27], the result from these efforts show that the background FLRW spacetime is a good approximation of the area distance in the observed universe [28, 29]. Independent studies based on general relativistic N-body simulation reached a similar conclusion [13, 30, 31]. However, these studies focused on the following redshift limit 0.023 ≤ z ≤ 1100 [13, 28, 30–32]. The focus on this redshift range was motivated by the fact that the SHoES collaboration and the Carnegie-Chicago Hubble Program (CCHP) truncated the sample of the peak magnitudes of the SN1A at z ≥ 0.02 [6, 9]. On the surface, this appears to be sufficiently motivated but on closer examination, it becomes clear that the determination of the Hubble rate using the peak magnitudes of SN1A within this redshift range (0.023 ≤ z ≤ 0.5) relies crucially on the geometric distance measurement of a set of anchors that are very nearby [6, 9]. Essentially, the calibrated absolute magnitude of the SN1A in the Hubble flow, could depend on the distance measurement to the anchors in the z ≤ 0.01 redshift range [33]. Such a dependence could manifest as a tension in absolute magnitude of the SN1A [34–36] if the anchors live in a local over-density with a non-trivial curvature.

To build a consistent cosmic distance ladder in a perturbed universe that captures the interplay between the geometric distance measurements to a set of anchors and the SN1A in (0.023 ≤ z ≤ 0.5) redshift range, we derive a very concise expression for the area distance that includes general relativistic corrections in a perturbed FLRW spacetime.
(...)
Using this expression, we show that at very small redshifts (limit where the redshift goes to zero), the monopole of the distance-redshift relation is determined by the rate of shear deformations of the local spacetime. Distance to the nearby anchors is not given by the FLRW spacetime since the rate of shear deformation tensor vanishes in an FLRW spacetime. We show that for a consistently calibrated zero-point of the distance modulus, the SHoES and CCHP teams should infer the same Hubble rates and the Hubble rate inferred by both teams corresponds to global volume expansion. Finally, by fitting the Alcock-Paczynski parameters [37] based on the FLRW spacetime to corresponding perturbed expression, we show that the Hubble rate determined this way is sensitive to the local environment.

PS : je rappelle (pour ceux qui ont suivi les discussions sur le sujet) que les équations moyennes de Buchert pour un espace-temps inhomogène sont analogues à celles de Friedmann pour un espace-temps homogène, à un terme de "backreaction" près, qui dépend de la variance du taux d'expansion local ET du "rate of shear".

[physeb2]

Bonjour Yves,

merci pour mettre cet article dans la discussion. C'est en effet interessant que les études de l'effet des perturbations ai été fait avec une limite de z=0.023 quand toute la chaine de calibration commence depuis les échelles locales et que ce sont justement les échelles tres affectées par le local Bulk Flow, la dynamique de l'amas et super amas local, sachant que les supernova sont pour beaucoup mesurées dans une petite region du ciel.

[yves95210]

Bonjour,

Une étude de plus, qui vient confirmer l'écart entre la valeur du paramètre (plutôt que constante...) de Hubble mesurée à partir de chandelles standard dans l'univers "récent" (mais allant quand-même jusqu'à z=2,26, soit il y a plus de 10 milliards d'années selon le modèle standard) et celle calculée à partir des observations du CMB par la mission Planck.
Voici la publication (dont Adam Riess est l'un des co-auteurs), et un article (en anglais) qui la résume :

The team used the Pantheon+ data to look at two different results. The supernova measure, Pantheon+ SH0ES, gives a Hubble parameter of 72 – 74 (km/s)/Mpc. The cosmic background measure, Pantheon+ Planck, gives a Hubble parameter of 66 – 68 (km/s)/Mpc. Both are very precise, and they contradict each other. The study confirms that the Hubble tension is real. It isn’t due to any error of measurement, and we can’t say that one or the other is wrong.

[Deedee81]

Salut,

Le JWST devrait apporter des informations précieuses (voire des réponses ?) mais on n'y est pas encore. Un peu de patience, il n'y a pas longtemps qu'il est en service (et en plus, faut analyser les observations).
Je suis sur que Tezcatlipoca donnera des informations .... dès qu'il y en aura.

[yves95210]

Le JWST devrait apporter des informations précieuses (voire des réponses ?) mais on n'y est pas encore.

Des informations ou de nouvelles données, certainement. En cosmologie, surtout au sujet de la formation des galaxies et des amas dans l'univers primitif (quelques centaines de millions d'années après le "big bang").
Des réponses au sujet des mesures non concordantes de H₀, peut-être pas car, au point où en en est aujourd'hui, il semble que les réponses ne peuvent être que du domaine de la théorie.

Je vois qu'il y a plusieurs programmes d'observation dédiés à ce problème prévus dans le cycle 1 du JWST. Mais il devient de plus en plus improbable que l'écart entre les mesures de H₀ soit causé par des erreurs systématiques de l'une ou l'autre méthode utilisée; même si le JWST permet des mesures plus précises, elles ne devraient faire que confirmer cet écart (en réduisant les marges d'incertitude). Sauf grosse surprise, bien sûr...

Et je ne sais pas si les observations du JWST permettront de répondre à une question cruciale : la mesure de la courbure spatiale moyenne dans l'univers récent, supposée nulle ou négligeable dans le modèle actuel, mais qu'on ne connaît pas précisément. D'après ce que j'avais pu lire, les théoriciens dont les modèles conduisent à une évolution vers une courbure négative significative(*) dans l'univers récent (depuis la formation des grandes structures), de plus en plus dominé par les vides cosmiques, attendent surtout les résultats d'Euclid comme "smoking gun".

(*) "significative" voulant dire ici plus importante que ce qu'autorise le modèle ΛCDM (et plus généralement les équations de Friedmann) à partir d'une courbure spatiale à l'époque du CMB comprise dans la marge d'incertitude des résultats de Planck.
Une courbure négative assez faible (mais non négligeable) pourrait suffire à expliquer la non-concordance entre les mesures de H₀. Il faudrait qu'elle soit plus importante (ce dont doutent même certains partisans des cosmologies non homogènes) pour remplacer Ω_Λ dans une équation de Friedmann "effective" (car valide seulement à l'époque actuelle, puisque le modèle n'évoluerait pas comme celui de Friedmann) : en effet cela nécessite un rapport ~0,3/0,7 entre Ω_m et Ω_k.
Quoi qu'il en soit, et pour illustrer la difficulté de mesurer cette courbure, même avec Ω_k=0,7 aujourd'hui le "rayon de courbure" devrait être de l'ordre de 130 milliards d'années-lumière (si je ne suis pas planté en le calculant à partir de H₀=70 km/s/Mpc). Et avec Ω_k=0,1 le rayon de courbure serait encore 7 fois plus grand...

Si courbure il y a, les plus grandes structures assez régulières pour qu'on puisse constater (statistiquement) une déformation de leur géométrie sont les vides cosmiques, mais il faudrait pouvoir délimiter leurs contours assez précisément^(**) pour vérifier si leur géométrie moyenne (obtenue sur un grand nombre de vides) qui devrait paraître sphérique si l'espace est "plat", l'est réellement. Alors que, si la courbure spatiale est assez importante, leur diamètre apparent suivant la ligne de visée (distance comobile radiale) doit être différent de leur diamètre perpendiculaire à la ligne de visée (distance comobile transverse).

(**) C'est peut-être quelque-chose que les observations du JWST pourraient faciliter, puisqu'elles devraient permettre de mieux connaître la densité (en nombre de galaxies) à la périphérie des vides. Mais je n'ai pas trouvé de programme d'observation dédié à cette question.

[Deedee81]

Des réponses au sujet des mesures non concordantes de H₀, peut-être pas car, au point où en en est aujourd'hui, il semble que les réponses ne peuvent être que du domaine de la théorie.

Oui, bien sûr, mais plusieurs articles que j'ai lu espéraient que les données permettraient de faire évoluer la théorie.... mais :

même si le JWST permet des mesures plus précises, elles ne devraient faire que confirmer cet écart (en réduisant les marges d'incertitude). Sauf grosse surprise, bien sûr...

Les mêmes articles "craignaient" la même chose.

Sur la courbure par contre je n'avais rien lu de récent. Merci pour ces explications.

[yves95210]

Quoi qu'il en soit, et pour illustrer la difficulté de mesurer cette courbure, même avec Ω_k=0,7 aujourd'hui le "rayon de courbure" devrait être de l'ordre de 130 milliards d'années-lumière (si je ne suis pas planté en le calculant à partir de H₀=70 km/s/Mpc). Et avec Ω_k=0,1 le rayon de courbure serait encore 7 fois plus grand...

Evidemment je me suis planté (même si ça ne change pas grand-chose sur le fond), et deux fois en plus : avec Ω_k=0,7 le "rayon de courbure" serait de l'ordre de 16 milliards d'années-lumière, et seulement 2,6 fois plus grand, un peu plus de 40 milliards d'a-l avec Ω_k=0,1. C'est déjà plus raisonnable.
J'ajoute qu'il s'agit d'une courbure négative et donc d'une géométrie hyperbolique, il ne faut pas confondre ça avec le rayon d'une sphère...

[physeb2]

Bonjour a toutes et tous,

Des réponses au sujet des mesures non concordantes de H0, peut-être pas car, au point où en en est aujourd'hui, il semble que les réponses ne peuvent être que du domaine de la théorie.

mon opinion est assez différente. Il se peut que la théorie soit la clef, mais on est loin d'avoir retiré tout effet systématiques.
Juste pour prendre un petit exemple du côté des SNIa et du CMB-BAO (pour faire de la parité):
-SNIa- Bien que le travail sur la standardisation des SNIa soit fait aussi bien qu'il se peut, les relations empiriques de corrections stretch-color (couleur au pic Vs étirement de la courbe de lumière ) ne sont pas bien compris, surtout les effets de la poussière, métalicité du compagnon ce qui peut avoir une évolution avec le redshift des relations. De même, pour aller vers quelque chose de plus terre a terre, la calibration locale des distances (parralaxe + céphéides) est loin d'être complètement parfaite. Les lignes de visées pour faire ces calibrations sont très loin d'être isotropes (ça c'est pas forcément changeable, notre Univeers local est ce qu'il est). Tout effet systématique sur les variations de potentiel de gravité locale et effets de mouvements relatifs ne sont pas simple a modéliser et peut engendrer certains problèmes. Et dans ce cas, ça affecte une grande partie des méthodes dites "directes". Je ne dis pas que c'est le cas, mais on n'est pas du totu sûr que non.
-CMB - BAO - L'échelle des BAO qui est mesurée dans les 2 cas dépend complètement de la détermination du rayon de l'horizon sonore au moment du découplage photon - baryons/leptons (donc moment du CMB). Il se calcul à partir de d'information de la Nucleosynthèse primordiale qui donne les densités relative de radiation et matière baryonique a un instant précis, puis on applique l'eevolution standards des relations avec un fluide brotropique jusqu'au découplage, dont le moment est également évalué par la physique statistique. Il peut y avoir plusieurs sources d'introduction d'effet systématiques dans ce processus. Une mauvaise évaluation de ce paramètre se propage sur d'autres et en particulier sur les évaluations de H₀ par le CMB et BAO. C'est d'ailleurs discuté dans le dernier papier de la collaboration eBOSS (figure 6 page 19 de l'articles https://www.researchgate.net/publica...nt_observatory)

Je dis seulement qu'il ne faut pas enterrer les effets systématiques trop tôt...ceux qui restent sont bien compliqués a prendre en compte

[yves95210]

Bonjour,

mon opinion est assez différente.

et certainement mieux fondée que la mienne.

Dans le même ordre d'idée que les problèmes que tu cites, il y a ce dont on avait parlé un peu plus haut dans cette discussion :

we show that at very small redshifts (limit where the redshift goes to zero), the monopole of the distance-redshift relation is determined by the rate of shear deformations of the local spacetime. Distance to the nearby anchors is not given by the FLRW spacetime since the rate of shear deformation tensor vanishes in an FLRW spacetime. We show that for a consistently calibrated zero-point of the distance modulus, the SHoES and CCHP teams should infer the same Hubble rates and the Hubble rate inferred by both teams corresponds to global volume expansion. Finally, by fitting the Alcock-Paczynski parameters [37] based on the FLRW spacetime to corresponding perturbed expression, we show that the Hubble rate determined this way is sensitive to the local environment.

Or il y a bien une solution théorique pour tenir compte (à toute échelle) du "rate of shear deformations", c'est le théorème de Buchert qui permet de calculer le taux d'expansion moyen d'un volume comobile selon une équation "à la Friedmann", mais contenant un terme supplémentaire (la backreaction) dépendant de la moyenne du rate of shear moyen et de la variance du taux d'expansion local sur le volume concerné. Suivant le signe de ce terme (négatif si le rate of shear est important), il peut avoir pour effet d'accélérer (si >0) ou de freiner l'expansion du volume.
Autant il n'est pas certain que la backreaction ait un effet important à grande échelle (à partir de l'échelle d'homogénéité), autant son effet ne peut certainement pas être négligé à la distance où se situent les barreaux intermédiaires de la cosmic distance ladder (quelques dizaines de Mpc). Cet effet (de freinage de l'expansion) décroît avec la distance puisque le rate of shear moyen est de plus en plus faible lorsque le volume concerné est de plus en plus grand (et homogène), jusqu'à l'échelle d'homogénéité (~150 Mpc, soit z~0,035).

[yves95210]

Bonjour,

Je ne savais pas trop où poster l'info sans ouvrir une nouvelle discussion, mais c'est sans-doute dans ce vieux fil qu'elle est la plus pertinente :

un papier de Stacy McGaugh (en cours de soumission) suggère que la tension entre les mesures locales du paramètre de Hubble H₀ et sa valeur calculée à partir des paramètres cosmologiques déterminés par Planck pourrait être due à une sous-estimation de l'impact des effets de lentille gravitationnelle causé par l'apparition de galaxies de l'univers primitif, anormalement précoces et/ou massives comparativement aux prédictions du modèle LambdaCDM sur lequel est basée l'interprétation des observations du CMB :

Les paramètres cosmologiques obtenus à partir des ajustements au spectre de puissance acoustique du fond diffus cosmologique se sont progressivement éloignés de la région de concordance spécifiée par des contraintes indépendantes, se déplaçant régulièrement le long d'une ligne de Ω_mh³ constant vers H₀ plus faible et Ω_m plus élevé. Cette migration est à l'origine de la tension actuelle avec la valeur mesurée localement de la constante de Hubble. Nous soulignons que cette migration est corrélée avec l'inclusion de multipoles plus élevés dans les ajustements, pour lesquels les effets de lentille gravitationnelle sont importants. L'apparition de galaxies anormalement massives dans l'univers primitif, comme l'indiquent les observations du JWST (et d'autres), suggère que l'impact de l'effet de lentille gravitationnelle sur le CMB pourrait être sous-estimé. Il est concevable que cela contribue à la migration temporelle des valeurs des paramètres cosmologiques les mieux adaptées et à la tension qui en résulte sur la valeur de la constante de Hubble. Si c'est le cas, c'est peut-être la valeur de H₀ issue des observations du CMB qui est systématiquement erronée plutôt que les déterminations locales.

Cela expliquerait pourquoi cette tension n'existait pas avec les premiers résultats de WMAP :

[JPL]

Intéressant. À suivre avec les progrès des observations à venir.

[yves95210]

En relisant le début de cette discussion, dont je ne me rappelais pas trop, je vois que physeb2 avait expliqué (au message 16) la différence entre les mesures de WMAP et celles de Planck. Mais sans y voir une éventuelle cause d'erreur systématique dans les mesures faites par Planck, ou plutôt dans les corrections apportées pour tenir compte des effets d'avant-plan sur le rayonnement du CMB :

La différence de mesure entre WMAP et PLANCK peut venir de pas mal de choses. Il s’agit de l’observation du même « objet physique », le CMB, mais avec des instruments un peu différents et aussi avec des méthodes d’analyses légèrement différentes.

Les deux quantités d’intérêt sont la température et la polarisation linéaire des photons qui nous parviennent depuis toutes les directions possibles. Afin de mesurer avec grande précision ces deux quantités il est absolument nécessaire de caractériser toutes les contaminations possibles, en particulier ce qu’on appelle les avants plan (forqegrounds en anglais).

Le CMB est un rayonnement thermique (donc suit une loi de corps noir) qui aujourd’hui s’observe avec une température d’environ 2,725 K ce qui correspond majoritairement a des photons millimétrique et sub-millimétrique. Dans ces longueurs d’onde on retrouve pas mal de source astrophysique et en premier lieu la poussière de notre galaxie qui contamine l’observation sur de tres grandes échelles ainsi que des sources compactes comme certaines étoiles et des amas de galaxies (mais aussi notre propre planète, raison pour laquelle on envoie le plus loin possible notre satellite).
(...)
Le nombre de fréquence pour PLANCK (30, 44, 70 Ghz pour LFI et 100, 143, 217, 353, 545 et 857 GHz) est plus important que pour WMAP (23, 33, 41, 61, et 94 GHz) et la précision est également plus grande. Tu peux voir que la contamination de la galaxie est franchement différente de pour les cartes de hautes fréquences qu’apporte PLANCK.

Ces différences font que les nécessités d'analyses furent différentes pour les deux satellites surtout pour les échelles angulaires plus petites. (...) La maniere de passer des cartes a ce spectre de puissance utilise des méthodes complexes qui doivent tenir compte des avant-plans pour chaque fréquence. Lorsque le travail est finit on obtient les points suivants pour les perturbations avec un modèle qui ajuste ces derniers:

Pièce jointe 434150

Dans ce cas le modele dépend typiquement de 7 paramètres dont fait partie. On peut voir que les points de WMAP s'arrêtent a quand ceux de PLANCK vont bien plus loin grâce au cartes de grandes fréquences. J'ai omis de dire que les grandes échelles angulaires correspondent aux petits , d'ailleurs la sphère entière, ce qu'on appelle le monopole, correspond a . Plus est grand et plus on regarde des taches de tailles plus petites. Notamment les échelles avec nécessitent qu'on nettoie les cartes des amas de galaxies pour être précis, chose que ne pouvait pas faire WMAP.

C'est en fait ce "nettoyage" qui serait en cause selon McGaugh, si le modèle de formation des galaxies et amas utilisé(*) n'est pas fidèle à la réalité, en particulier parce qu'il ne permet pas la formation assez rapide de galaxies aussi nombreuses / massives que ce qu'on observe - surtout récemment avec le JWST dont les découvertes en la matière ont fait pas mal de bruit même si toutes n'ont pas été confirmées par spectroscopie.

(*) Lui-même basé sur le modèle LambdaCDM, ce qui fait un peu raisonnement circulaire quand l'objectif est de confirmer la validité de ce dernier ou d'en déterminer les paramètres.

Mais si d'autres observations confirment que le modèle de formation des structures doit être revu, et probablement avec lui certains piliers du modèle LambdaCDM dont il dépend, c'est un sacré chantier théorique (qui donnera lieu à pas mal de controverses) et on n'est pas près d'avoir le fin mot de l'histoire...