Bonjour,
j'ai fait tourner par MCMC un modèle de Brans-Dicke "basique" où je sample sur les paramètres Omega_m, Omega_k, Omega_BD, H0, Ps_i0 = G*Phi_0 avec Phi_0 le potentiel de Brans-Dicke, F_0 = (d(Phi)/dt/Phi)_0 et omega_BD le paramètre propre à Brans-Dicke.
On a la relation :
et la relation de closure :
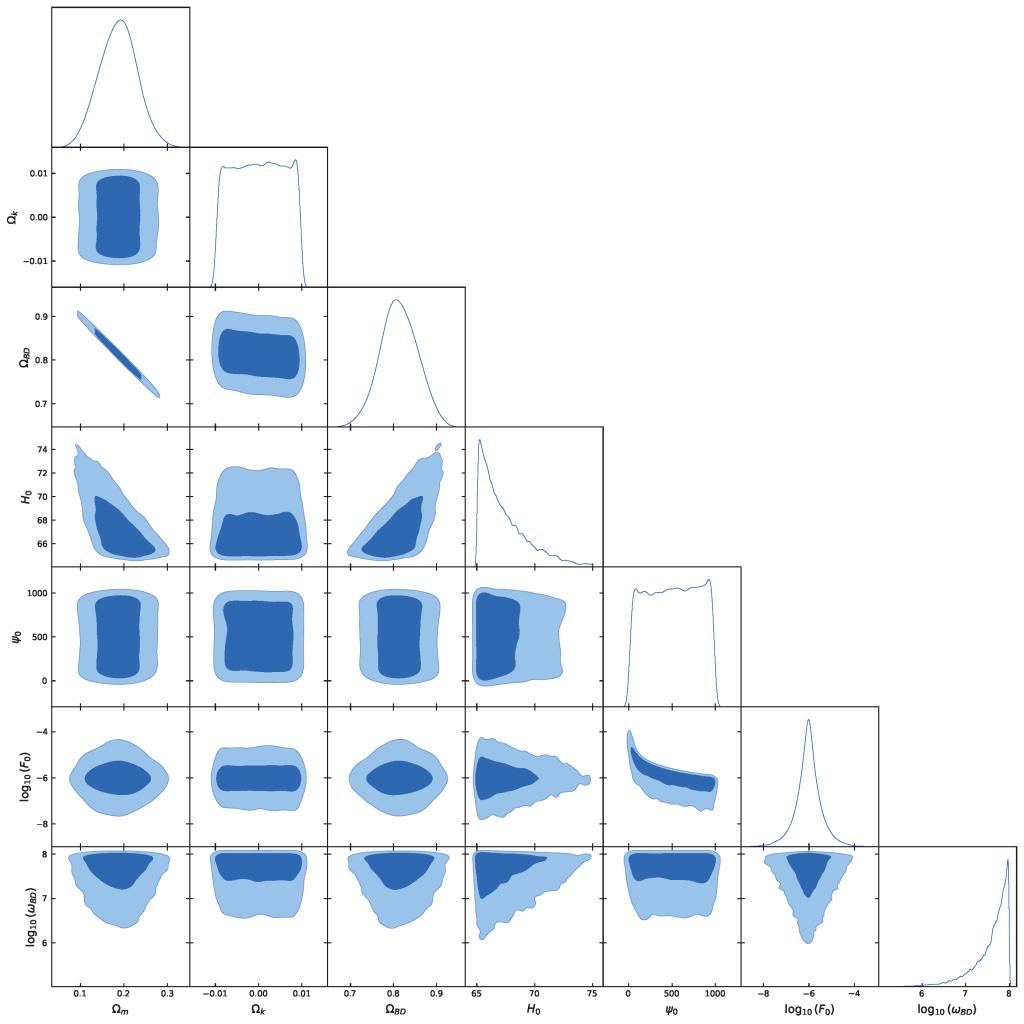
J'obtiens les contours suivants :
J'obtiens des dégénérescences sur Psi_0 : je ne sais pas comment la briser, j'ai besoin d'hypothèses supplémentaires que je ne connais pas pour l'instant afin d'essayer de mieux contraindre la relation de proportionnalité entre le potentiel de Brans-Dicke Phi_O et la constante de gravitation G.
Comme avec Planck, il y a aussi une dégénérescence sur Omega_k où l'on ne peut pas trancher sur un univers fermé ou ouvert.
J'ai aussi un problème avec les contours de H0 et de omega_BD : impossible pour l'instant d'obtenir de jolies gaussiennes sur les erreurs des. best-fit obtenus.
Par example, j'ai mis les priors suivants :
Quelles seraient d'après-vous les hypothèses potentiellement intéressantes pour briser ces dégénérescences concernant H0, Psi_0 et omega_BD.Code:param_names = ["Omega_m", "Omega_k", "H0", "Phi_0", "d_Phi_0", "omega_BD"] lower_boundaries = np.array([[0.05, -1e-2, 65.0, 1e-3 / G, 1e-3 / (-H0 * G), 4e4]]) upper_boundaries = np.array([[0.35, 1e-2, 75.0, 1e3 / G, 0, 1e8]])
Un des résultats intéressants dans ces calculs est l'anti-corrélation entre Omega_BD et Omega_m , ce qui me permet de me passer d'une constante cosmologique mais le problème est que j'obtiens un best-fit Omega_m = 0.22, ce qui est trop faible par rapport au modèle de concordance LCDM qui est
en faveur d'un Omega_m plutôt proche de Omega_m = 0.3.
Toute aide est la bienvenue,
Cordialement
-----