Hello
Tout le monde est au courant qu'une masse modifie l'écoulement local du temps
Quand on est au centre de la Terre, placée dans un espace plat, cet écoulement dépend de la masse de la Terre, contrairement à l'infini de la Terre. Dans les deux cas on flotte, mais la relativité distingue ces deux expériences: le champs d'accélération n'est pas nul au centre tandis qu'il est nul à l'infini
Si on calcule le champs d'accélération de la masse de l'univers observable (on est au centre) en intégrant G.M/r² = G(ρ.4π.r².dr)/r² entre 0 et le rayon de l'univers observable, on trouve 4πG.ρ.R. Avec ρ=1.1E-27kg/m3 et R=13.7Mda, on trouve 1.2E-10m/s², soit l'accélération de Milgrom a0 du modèle MOND:
Finalement, on pourrait donc dire que la matière noire n'est qu'une illusion due à l'effet relativiste de la masse de l'univers observable, il n'y aurait donc pas plus de matière noire que de beurre en broche. Dans le cas des galaxies observées sans matière noire comme DF2 & DF4, il faut tenir compte du facteur (1-v²/c²-H/d)^1/2: comme ces galaxies sont véloces, tout se passe comme si l'effet était plus proche du centre (v² VS 1/d, si v est 2 à 4fois plus rapide qu'une vitesse d'orbite de l'amas local, tout se passe comme si le champs local, en 1/d², est 16 à 256fois plus fort), là où a0 devient alors faible et négligeable devant le champs de ces galaxies, comme s'il n'y a donc pas d'effet 'matière noire'
Mais alors comment les cosmologistes en sont arrivés à penser que la matière noire est bien réelle? Ca viendrait de l'hypothèse du modèle, à savoir Einstein-De Sitter, où l'on néglige localement l'expansion ainsi que la gravitation (moins forte que que l'expansion), où l'espace est donc supposé localement plat. Et comme a0 est très faible et que l'espace est mesuré plat dans son ensemble, ils pensent que l'approximation est valable et qu'ils peuvent faire des simulations Newtoniennes, dans lesquelles l'espace est alors supposé plat, et où il faut donc rajouter de la matière noire pour compenser ces commodes hypothèses. Actuellement a0 est mesurée dans les galaxies mais reste inexpliquée, sans lien avec l'univers observable. On peut aussi entendre parler du théorème de Birkhoff, mais là, ils faudrait qu'ils le relisent: ce théorème n'est valable qu'à l'infini, asymptotiquement, à croire qu'ils confondent la valeur strictement nulle (ici même) du champs gravitationnel de l'univers (l'univers au delà de l'univers observable), par définition (tout ce qui est en dehors de l'univers observable ne nous a pas encore atteint), avec la valeur nulle du champs de l'univers observable à l'infini, par définition (la masse de l'univers observable est finie), alors qu'il faut considérer la valeur du champs de l'univers observable en son centre, par définition aussi (nous sommes toujours au centre de notre univers observable)
De plus, avec une densité ρ=1.1E-27kg/m3, on est en dessous de la densité critique ρ=1E-26 de l'espace plat, il devient alors inutile de chercher la matière baryonique manquante
Voilà voilà, j'ai tenté de faire paraître cette belle idée, mais je ne suis pas affilié à un quelconque labo donc mon article est ignoré et non lu (si j'ai bien compris le fonctionnement des revues peer-review). Mais je viens apporter la bonne nouvelle! Mystère résolu!
-----



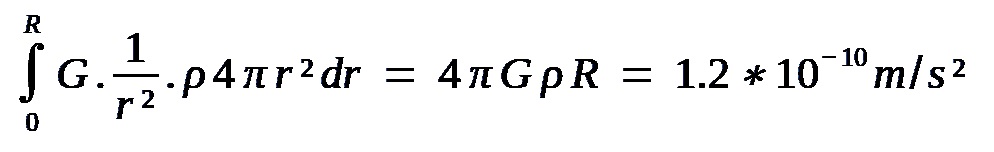

 " : écart de fréquence entre deux points distants de h (en altitude) ; on voit bien apparaitre l'énergie potentielle massique gh
" : écart de fréquence entre deux points distants de h (en altitude) ; on voit bien apparaitre l'énergie potentielle massique gh