cristallographie

[anamir-22]

bonjour a tous, pour quoi il existe des systèmes cristallins ayants pas certains modes de réseaux??? par exemple : pour quoi il n'y a pas un quadrature à bases centrées ou bien à faces centrées.
-----

[ArtAttack]

Y a deux règles d'or, pour résumer :
- La maille doit avoir le volume le plus petit
- La maille doit considérer et respecter les opérations de symétrie
Illustration

[anamir-22]

dacord , mais dans ce lien que tu ma vient de donner il y a un quadrature a faces centrées!!!

[mach3]

il y a un quadrature a faces centrées!!!

non je n'ai pas vu de quadrature a face centrées moi. Par contre j'ai vu un quadratique centré, c'est à dire de mode I.

Il n'y a pas de quadratique à face centré, car c'est équivalent à un quadratique centré. Tout réseau quadratique centré peut se décrire comme un quadratique à face centrée et inversement. On ne garde donc qu'un seul des deux, le plus simple.
Il suffit de faire un petit dessin pour s'en convaincre.

m@ch3

[A voir en vidéo sur Futura]

[anamir-22]

mais comment on peut dire qu'ils sont équivalent??? le quadratique à faces centrées contient 4 motif/maille, et le quadratique centré contient 2 motif/maille.

[mach3]

une maille quadratique centré contient déjà toutes les informations nécessaire à décrire le réseau. Si je construis une maille quadratique à face centrée à partir de cette maille centrée, je vais décrire le même réseau, mais cette maille contient des informations redondantes (2 fois plus de motifs) qui ne sont pas utiles. Je crois que je ne pourrais pas faire l'économie d'un schéma pour te faire comprendre...

m@ch3

[anamir-22]

non vous etes pas obliger, et si tu peut me donner une réponse directe pour ce petit exercice ""les réseaux de Bravais de la maille quadratique sont P et I, montrer pourquoi la maille quadratique ne possède ni mode F ni C"", par ce que j'ai un petit problème dans la production.

[mach3]

Bon ben trop tard, c'est fait, et cela répond à une partie de ton exercice :



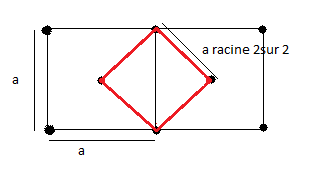
Le schéma représente 4 mailles quadratiques centrée, vues selon l'axe c. Les ronds noirs sont les noeuds de la maille primitive et les ronds blancs sont les noeuds introduits par le mode I, ils ont pour coordonnées réduites 1/2, 1/2, 1/2. On voit très bien qu'on peut choisir une autre maille, celle en pointillés, qui est quadratique à faces centrées et de volume double de la maille centrée de départ. Choisir cette maille n'apporte rien de plus, car la maille centrée décrit déjà parfaitement le réseau.
On peut faire le raisonnement inverse en dessinant un réseau quadratique à face centrée et constater qu'on arrive aussi bien à le décrire par une maille centrée qui fait la moitié de son volume.

L'inexistence du mode C se montre de la même façon, en partant de 4 mailles quadratiques primitives.

m@ch3

[anamir-22]

oui c'est convainquant, mais comme je t'ai deja dit, j'ai un problème de production, comment je peut répondre à ce genre des questions?

[anamir-22]

oui bien c'est convainquant, mais comme je t'ai déja dit que j'ai un problème de production, comment donc je peut répondre à ce genre des questions?

[mach3]

Tu fais un schéma et tu expliques avec tes propres mots. Si tu as bien compris, ce ne sera pas difficile. Toujours est-il qu'on ne peut pas le faire à ta place. Par contre tu peux essayer de faire une réponse ici, on essaiera de corriger et/ou de te conseiller.

m@ch3

[anamir-22]

dacord, donc ma réponse seras comme suit: je design une maille CFC/CS et j'ajoute des noeuds de tel manière à obtenir une maille quadratique, à la fin j'aurais un quadratique centré/simple, et j'écris un petit commentaire "on part d'un CFC/CS on ajoute des noeuds en respectant la symétrie de la maille, on trouve alors un quadratique centré/simple de paramètres de maille ..., et de là on peut dire que la maille quadratique ne possède ni mode F ni mode C".

[anamir-22]

donc ma réponse sera comme suit:
je design une maille CFC/CS et j'ajoute des noeuds de tel sorte d'obtenir un quadratique, à la fin j'aurais un quadratique centré/simple. j'écris un petit commentaire " on part d'un CFC/CS et on ajoute des noeuds en respectant la symétrie de la maille, on trouve alors un quadrature centré/simple, et de la on peut dire qu'un quadratique ne possède que les modes P et I".
est ce que c'est juste???

[mach3]

Pardon, je t'avais oublié.

Je ne comprends pas ce que viennent faire un cubique face centré et un cubique simple dans l'explication...

m@ch3

[anamir-22]

comme j'ai dit, on part d'un CFC ou bien d'un CS, en les considérant comme les mailles ayants les critères exactes(la forme la plus simple et le volume le plus petit possible), on ajoute donc des noeuds de tel sorte à trouver un quadratique, et donc on trouveras le quadratique ayant la forme la plus simple et le volume le plus simple.

[ArtAttack]

La cristallo c'est pas de la cuisine où on ajoute des nœuds comme ça.
Aucun rapport entre un quadratique et un cubique, sinon des axes de symétrie d'ordre 4 entre autres.

[anamir-22]

On n'ajoute pas les sites comme ça arbitrairement, mais respectant la symétrie de la maille.

[mach3]

Le problème c'est qu'à partir d'un cubique, tu ne peux pas générer tous les quadratiques possibles (tous les rapports c/a possibles) en ajoutant des noeuds, donc tu perds toute généralité. Tu ne fais que montrer (et encore, ça me parait vaseux...) que les quadratiques qui peuvent être issus d'un cubique (pas les autres!) ne peuvent être que P et I. Parler des cubiques est hors-sujet. Est-ce que j'en ai parlé moi pour te faire comprendre pourquoi un quadratique n'admet pas de mode C ou F ?

m@ch3

[anamir-22]

http://www.google.fr/url?sa=t&rct=j&...RSTsaQ&cad=rja
consultez ce lien, lire la dernière paragraphe de la deuxième page pour voir pourquoi on ajoute des noeuds à une maille.

[ArtAttack]

Tu comptes reproduire les réseaux de Bravais à partir des 7 principaux systèmes ?
Désolé c'est déjà fait.

[anamir-22]

Donc c'est mieux de dire directement que l'idée n'est pas valable, et de me donner un peu d'aide.

[mach3]

Donc c'est mieux de dire directement que l'idée n'est pas valable, et de me donner un peu d'aide.

mon explication et mon schéma ne te plaisent pas? on ne va pas faire le travail à ta place. Soit tu as compris et tu es capable d'expliquer, soit tu n'as pas compris et dans ce cas, dis nous ce que tu n'as pas compris exactement. Qu'est ce qui n'est pas clair?

m@ch3

[anamir-22]

Dans ton schéma tu as commencé par 4 cubes de type C, et donc tu n'as pas respecté deux règles:
1- la forme la plus simple possible.
2- le volume le plus petit possible.

et pour respecter ces deux règles, je me propose le schéma suivant:

[mach3]

Dans ton schéma tu as commencé par 4 cubes de type C, et donc tu n'as pas respecté deux règles:

je n'ai pas fait des cubes, mais des mailles quadratiques vu de dessus selon l'axe c, et, de plus je n'ai certainement pas représenté un mode C. Je l'ai quand même précisé il me semble et j'ai même mis les cotes en coordonnées réduites. J'en déduis donc que vous n'avez rien compris à mon schéma et que les lacunes sont ici...

Les quatre mailles quadratiques que j'ai dessinées cote à cote sont de paramètres . La maille quadratique est un prisme à base carré. La base carrée à pour longueur de coté "a", et la hauteur du prisme est "c".
Dans ma projection, on peut aisément lire graphiquement les coordonnées x et y des noeuds, en revanche on ne peut pas lire la côte z (c'est à dire la hauteur à laquelle les noeuds sont situé au-dessus du schéma). J'ai donc indiqué que les noeuds en noir était en z=0 et z=1, alors que les noeuds en blanc étaient en z=1/2. x, y et z sont évidemment les coordonnées réduites. x varie de 0 à 1 le long de la longueur a, y le long de b et z le long de c. Quand on dit z=0 ou 1, cela signifie donc, dans la projection suivant c, que le noeud se situe dans le plan de la feuille, et donc par symétrie de translation à une distance c au dessus de la feuille (mais aussi 2c, 3c, -c, -2c, etc...). Quand on a z=1/2, cela signifie que le noeud est situé à une distance c/2 au dessus de la feuille (mais aussi, par symétrie 3c/2, 5c/2, -c/2, -3c/2, etc), donc à mi-distance par rapport à ceux qui sont en z=1.
Les noeuds représentés en blanc sur le schéma sont donc exactement au milieu de la maille quadratique considérée (ils sont visiblement en x=1/2 et y=1/2 et j'indique dans ma légende qu'ils sont en z=1/2), et celle-ci est donc centrée (et non base centrée, sinon, j'aurais représenté ces noeuds en noir, pour signifier qu'ils étaient dans le plan de la feuille comme les autres, et non en blanc).
Ma maille quadratique centrée est bien la plus petite possible qui respecte les symétries du réseau. Si j'essaie d'en choisir une plus petite, qui ne contient qu'un seul noeud au lieu de 2, je perds à coup sûr la symétrie d'ordre 4 car j’obtiens une maille triclinique primitive.

Si maintenant je considère la maille quadratique représentée en pointillée, de paramètres . Je vois qu'elle présente le noeud primitif, en x'=0, y'=0, z'=0, mais aussi les 3 noeuds supplémentaires du mode F (1/2 1/2 0, 1/2 0 1/2, 0 1/2 1/2). Cependant, je peux choisir la maille quadratique de mode I précédemment décrite pour caractériser le même réseau. Je réduis ainsi le volume de la maille par 2, tout en sauvegardant mon axe de symétrie d'ordre 4.

m@ch3

[anamir-22]

d'abord merci de toute ces explications, mais le schéma que vous avez présenté montre l'existence du mode quadratique centré.

[mach3]

mais le schéma que vous avez présenté montre l'existence du mode quadratique centré.

on peut en tirer deux choses :
-la maille quadratique centrée existe, car on ne peut pas la réduire à une maille quadratique primitive (la réduction à un mode primitif mène à une maille triclinique)
-la maille quadratique à faces centrées n'existe pas, car on peut la réduire à une maille quadratique centrée

En faisant le même schéma, mais en supprimant les noeuds blancs on en tire que la maille quadratique à base centrée (C) n'existe pas, car on peut la réduire à une quadratique primitive.

m@ch3

[anamir-22]

et je te remercie encore une fois.

[KRSone]

Bonjour,

J'ai une question plus simple.
On me dit qu'un cristal peut être décrit par son réseau et son motif.

Dans l'aide mémoire science des matériau il est dit cela :

Un réseau cristallin est un ensemble 3D de pt imaginaires. Il peut être généré par répétition, un nombre entier de fois, de trois vecteurs de base qui définissent une maille élémentaire du réseau d'origine arbitraire...

Motif atomique :
C'est un ensemble d'atomes, avec leur position relative, qui doit être reporté en chaque nœud du réseau pour reconstituer exactement la totalité des atomes du cristal.

Je ne comprend pas et ne vois pas la différence entre le motif et la maille. Les deux notions sont proches je ne parviens pas à faire la différence.