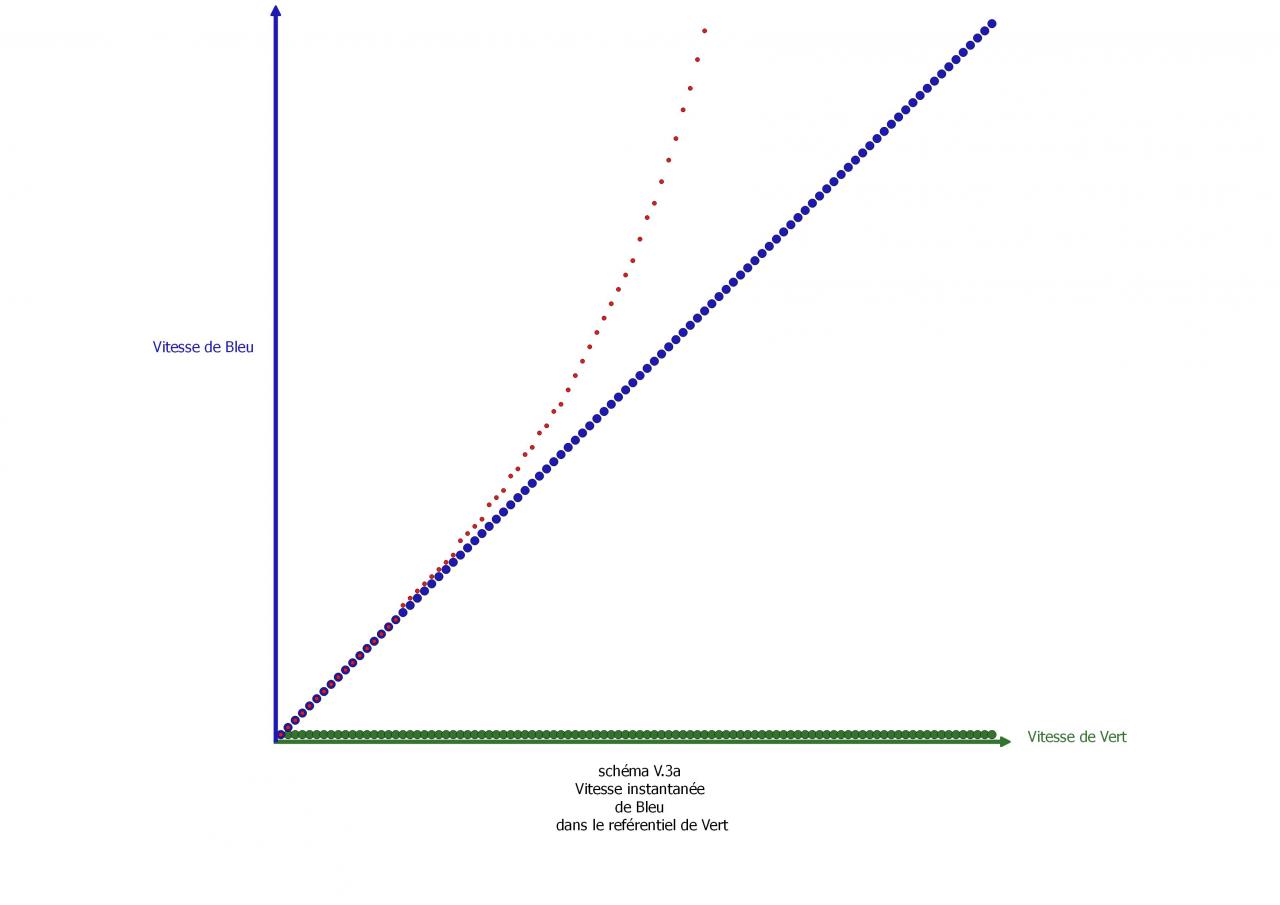
Bonjour
pour un TN de Schwarzschild
la Vitesse de satellisation est donné par la formule :
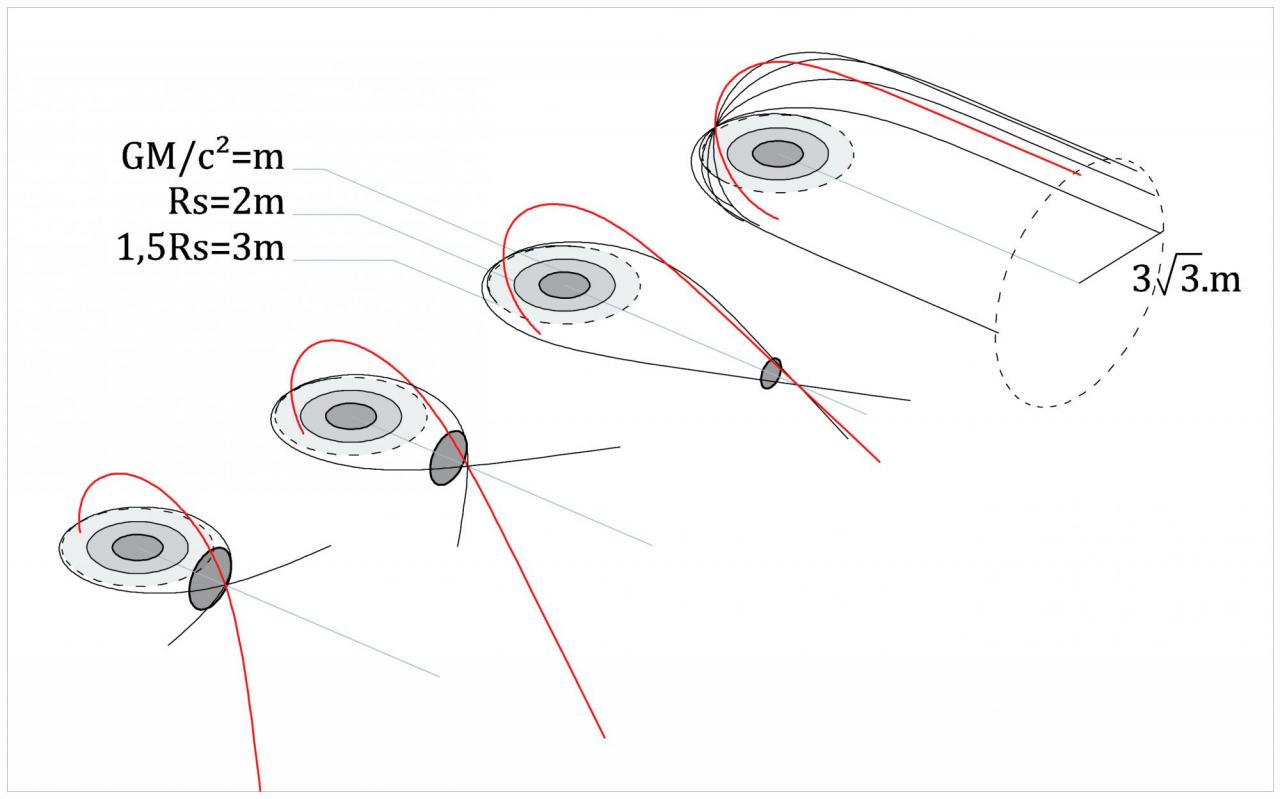
pour Vsat = c on trouve R= 1.5 Rs
Normalement un observateur en orbite autour du TN ne verra pas sa silouhette comme une sphère de 3Rs de diamètre mais comme une ellipsoïde (ellipse doppler) et ce à cause de l'aberration de la lumière.
pour un TN de Kerr :
comment calculer la vitesse de satellisation, comment se présente une orbite dans le cas d'un TN de Kerr?
comment voit un observateur stationnaire la silouhette du TN de Kerr?
comment voit un observateur la silouhette du TN de Kerr lorsqu'il se trouve en orbite géostationnaire?
merci pour vos réponses.
-----






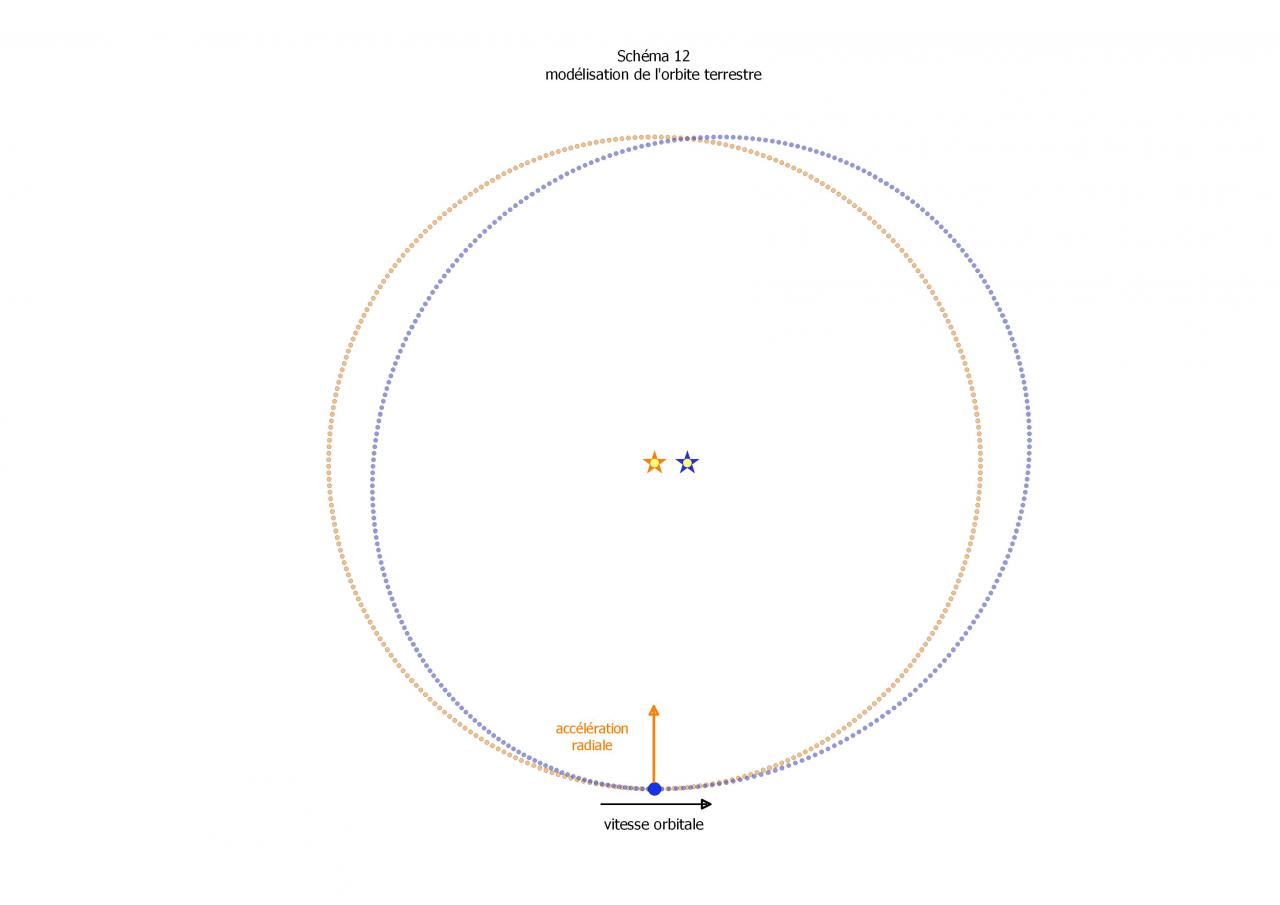


 ( faut le prendre avec humour)
( faut le prendre avec humour)