salut a tous svp je veux dexplication
j'ai un projet de realise un oscillateur lc a base de amplificateur operationnel a proteus é jai essaye voila le schema mais quand je simule la sortie va donne un signal non sinusoidal (carre) a cause du gain de implificateur va etre superieur a 1 et ça le probleme jai pas compre cette explication du gain
-----






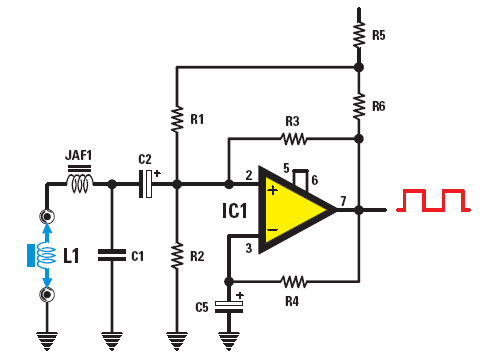
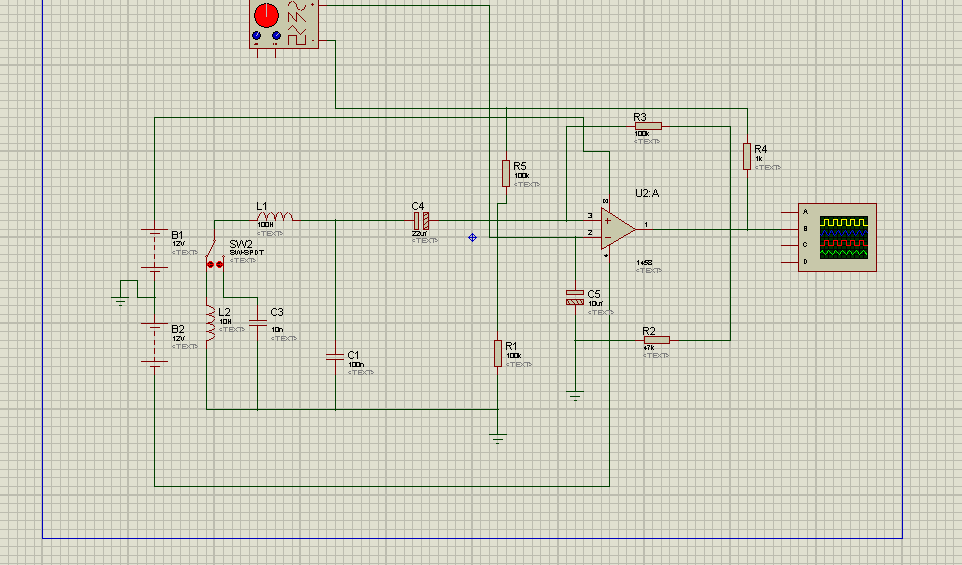 sa ce que je ai accompli
sa ce que je ai accompli