[Sixième] Vecteurs, rebond, etc...

[Aenonis]

Bonjour,

Je me penche sur un problème de sixième (en France, étant Belge, ce n'est pas la même pour moi, en Belgique, c'est la première secondaire).

Je vous pose le problème:
Les éléments se situent dans le plan à deux dimensions .
J'ai un cercle de centre et de rayon .
J'ai un segment aux extrémités , .
Le cercle se déplace dans le plan selon le vecteur qui pointe vers (la vitesse est incluse dans ce vecteur).

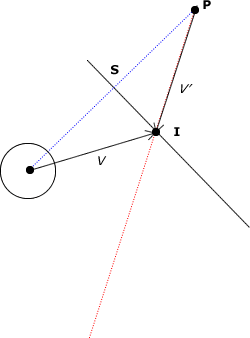
Lorsque le cercle rentre en collision avec le segment, j'aimerai trouver une formule (avec les éléments susmentionnés) qui renvoie le vecteur qui sera le vecteur de déplacement du cercle après le rebond.

Au plaisir d'avoir de vos nouvelles,

Aenonis
-----

[Bruno]

Bonjour,

Ça dépend un peu de comment le cercle rebondit. Est-ce qu'il se comporte comment un rayon réfléchi, est-ce qu'il ya du frottement, etc... ?

[Aenonis]

Pour répondre à ta question:
- Frottement nul.
- Le rebond se comporte comme la réflexion optique.

Désolé pour les imprécisions...

Au plaisir,

Aenonis

[Bruno]

Dans ce cas on peut utiliser la méthode des images pour construire V'. Ça nécessite de calculer un point image P, puis I l'intersection entre S et la trajectoire du cercle, en déduire un vecteur v_IP (cf schéma), le normer et on trouve V' en le multipliant par la norme de V.

[A voir en vidéo sur Futura]

[Aenonis]

Je peux calculer , mais j'ai un soucis pour la suite.

En transformant le segment en droite , j'obtiens pour valeurs:


Et en appliquant la formule de symétrie d'un point par rapport à une droite, j'obtiens:



Pour éviter le cas insidieux du segment vertical (menant à une droite indéterminée), on peut injecter et dans les formules de et :

Voici les formules finales:



Question: peut-on simplifier ce machin?

Question deuzio: quelle est la formule pour obtenir le point ?

Merci de vos réponses,

Aenonis

[Bruno]

J'ai pas vérifié les formules finales. Si tu cherches une formule toute faite V'=f(ax, bx, ay, by, ...), tu risques de te heurter aux cas particulier où il n'y a pas de solution. En fait, cette formule n'existe probablement pas et il faut se contenter d'une discussion, en s'aidant par exemple du produit vectoriel entre V et S qui sera nul dans le cas pathologique où le cercle se déplace parallèlement à S. J'imagine que c'est pour implémenter ça dans un programme ?

Pour le point I, c'est l'intersection de deux droites dont tu connais les équations paramétriques à partir de tes données. Donc ça revient à résoudre un système de 2 équations à 2 inconnues.

[gg0]

Ben dis donc !!

On est sacrément fort, en première secondaire belge (*) !!!
En France, de nombreux étudiants seraient "secs" devant ce genre de question.

Cordialement.

(*) ou sixième en France. âge des élèves 11 ans.

[Bruno]

Je crois qu'il voulait parler de la sixième secondaire belge (aka rhéto ) qui est la terminale française. Ou alors le niveau de l'enseignement francophone a tellement baissé qu'il est revenu à un niveau jamais atteint...

[gg0]

pour moi, en Belgique, c'est la première secondaire

Je n'ai fait que lire (et avoir fréquenté un forum Belge).

Cordialement.

[Aenonis]

Je crois qu'il voulait parler de la sixième secondaire belge (aka rhéto ) qui est la terminale française. Ou alors le niveau de l'enseignement francophone a tellement baissé qu'il est revenu à un niveau jamais atteint...

Ce n'est pas moi qui ait qualifié cet exercice de sixième française: c'est lui.

Maintenant que vous me le dites, c'est vrai que ça m'a l'air compliqué pour des têtes blondes de 11 ans...

Mais sinon, oui, c'est pour mettre dans un programme .

Aenonis

[gg0]

J'ai trouvé la référence :

C'est un problème de symétrie du niveau 6ème. (Zartan)

Pour autant que j'aie compris le contexte, il s'agissait d'un élément partiel (utiliser une symétrie) et pas du problème général. Mais Zartan poussait un peu en qualifiant de niveau 6ème. Il a dû oublier ce qu'on y fait (on y étudie effectivement des symétries, mais dans des contextes ultra-simples.

Bonne chance !

[Zartan]

Puisque je suis interpellé, j'ai affirmé cela d'après ce lien : http://www.lapasserelle.com/cours-en...ies/index.html

Ensuite j'ai orienté Anenonis ici puisqu'effectivement on a le schéma mais pas les formules

Ceci dit je pense qu'il lui suffirait d'inclure les masses dans ses formules et d'assigner une masse élevée aux bords.

[gg0]

Pas de problème, Zartan !

J'ai moi aussi l'habitude de qualifier par des niveaux les bases des questions. Mais entre la notion de base et son utilisation dans un contexte compliqué, il y a un monde.

Cordialement.

[Aenonis]

Re les gars ^^

Bon, le rebond d'un cercle sur un segment ça roule comme sur des roulettes, ça fonctionne parfaitement, je ne vais pas mettre les calculs ici, ils sont à dormir debout, mais je voulais te remercier pour le schéma, il m'a super bien aidé!

Maintenant, j'aurai besoin de la formule (ou un schéma) qui simule le rebond entre deux cercles quelconques en mouvement qui se percutent.

À savoir:
- Les deux cercles ont des rayons quelconques (donc différents ou égaux).
- Il faut que la propriété du transfert d'énergie soit vérifiée: si un cercle c1 se déplace selon un vecteur v1 et qu'il percute un cercle c2 qui se déplace selon un vecteur v2, après la collision, c1 devra être v2 et c2 devra être v1.
- Ce serait génial si, comme pour le rebond du cercle sur le segment, le résultat soit indépendant des rayons.

Je vous remercie,

Aenonis

[Aenonis]

Pas de réponse?

[Aenonis]

Personne ne sait m'aider?

[Aenonis]

Alors? toujours pas de solution à me proposer?

[Bruno]

Le choc entre deux billes est plus compliqué et la position du choc dépend clairement des rayons. A priori, il faudrait poser les équations cartésiennes des deux cercles, leur centre dépendant alors d'un paramètre (le temps), et essayer de déterminer analytiquement ou numériquement la valeur de t pour laquelle le système a une unique intersection.

[Aenonis]

Le temps?

Mes cercles se déplacent... et quand il y a collision, je les fait rebondir...

Et je ne vois vraiment pas ce que le temps vient faire là dedans...

[Bruno]

Il faut bien un paramètre pour indexer les positions successives des cercles. Si les 2 cercles ont des vitesses différentes, on ne peut pas s'en passer si on souhaite calculer leur choc.

[Aenonis]

ok...

il faut que je revoie toute l'analyse du programme...

tu pourrais me dessiner un schéma?

[Bruno]

Tu n'as quand même pas besoin de moi pour dessiner deux cercles, deux positions initiales et deux vecteurs vitesse...

[Aenonis]

Bonjour à toutes et à tous,

Je me suis replongé dans les formules et je suis coincé.

Je viens de réécrire la partie du programme qui gère le rebond entre deux cercles.

J'ai calculé les vecteurs qui partent des centres du cercle au point de contact.

Et après, je ne sais pas comment je dois faire pour changer les vecteurs vitesse des deux cercles...

ça rebondit mais ça part en sucette...

Merci de m'aider .

Aenonis

[Aenonis]

je demande un up !

[Teddy-mension]

je demande un up !

Soyez patient, ce que vous demandez n'est pas simple, et à plus forte raison pour un élève du secondaire français, pour lequel le problème tend plus vers l'exo d'olympiade tortueux.

___________

Je ne sais pas où vous en êtes personnellement dans votre problème, mais je vais essayer de vous aider.

Donc si j'ai bien compris la situation :

Vous avez deux cercles.
On nomme le premier , de centre initial , de rayon et qui se déplace selon le vecteur vitesse .
On nomme le second , de centre initial , de rayon et qui se déplace selon le vecteur vitesse .

On nomme la position du centre de en fonction du temps, et celle de .
On a alors simplement :



On en déduit les équations des deux cercles en fonction du temps :


Maintenant, il s'agit de trouver le plus petit tel que les deux cercles aient un seul point d'intersection en commun. Là est tout le problème, parce qu'on ne peut tester toutes les valeurs de (peut-être obtenir un approché par dichotomie ?). M'enfin, j'ai l'impression que vous êtes passé outre, étant donné que vous savez à quel moment vos cercles se cognent.
On appelle ce temps.

Il ne vous reste plus qu'à déterminer l'équation de la médiatrice du segment reliant les centres de tvos deux cercles, qui auront alors pour coordonnées respectives et .
Pour chaque cercle, le rebond causé par le choc équivaudra alors à un rebond sur la médiatrice, et on se ramène au cas 1.

Pour les normes, il vous suffira d'échanger celles des vecteurs vitesse initiaux.

[Aenonis]

Je vous remercie.

Je teste tout ça, je met ça en pratique et je reviens ici.

Encore mille mercis .

Aenonis

[Aenonis]

Je viens d'analyser la solution que vous me proposez.

Le truc que j'ai oublié de dire, c'est que le centre du cercle bouge dans mon application.

À intervalle de temps régulier, les deux centres bougent selon le vecteur vitesse.

Je teste à chaque intervalle si les deux cercles sont en collision, s'ils le sont, je calcule le point d'intersection et j'essaye de faire rebondir.

Pouvez-vous m'aider à traduire ce que je viens d'énoncer en calculs mathématiques ?

Le temps n'intervient pas dans mes calculs vu que c'est une variable intrinsèque à l'application.

Au plaisir,

Aenonis

[Teddy-mension]

Le truc que j'ai oublié de dire, c'est que le centre du cercle bouge dans mon application.
À intervalle de temps régulier, les deux centres bougent selon le vecteur vitesse.
[...]
Le temps n'intervient pas dans mes calculs vu que c'est une variable intrinsèque à l'application.

Je n'arrive pas vraiment à saisir ce que manigance votre application. Pour moi, il y a deux cas :

Cas 1

Soit, à chaque intervalle de temps, qu'on nommera , votre application vous donne la position de vos centres des deux cercles (qui se sont chacun déplacé selon leur vecteur vitesse respectif), et vous utilisez seulement ces données (la "nouvelle" position des deux centres, donc !) pour poursuivre vos calculs. Entre autres, vous définissez un éventuel point d'intersection entre les deux cercles.

Dans ce cas là, le programme que vous allez écrire de votre côté pour simuler le rebond ne va pas effectivement pas contenir de variable de temps. Il va seulement exploiter les données que va lui fournir l'application à chaque .

Je teste à chaque intervalle si les deux cercles sont en collision, s'ils le sont, je calcule le point d'intersection et j'essaye de faire rebondir.

Mais, ici, un problème majeur de précision se présente, puisque les deux cercles peuvent très bien ne pas avoir un point d'intersection à un instant , ni à un instant , mais se cogner pendant ces deux instants.
C'est ce qui va arriver la plupart du temps d'ailleurs, ce qui m'amène à penser que vous ne vous situez pas dans ce cas là (en tout cas j'espère, sinon votre programme n'est pas efficace du tout).

On en arrive alors au cas 2.

Cas 2

C'est directement à vous de trouver l'instant (avec une précision relative, hein) où vos cerclent se rentrent dedans. Pour ce faire, il faut donc connaître à chaque instant la position de chaque cercle. Et dans ce cas-là, je vous renvoie directement à mes équations dans lesquelles j'ai pris en compte l'influence du temps sur la position des centres respectifs :

On nomme la position du centre de en fonction du temps, et celle de .
On a alors simplement :

Avec ça, on sait exactement où se situent le centre de chaque cercle en fonction du temps.
Par exemple, si chaque centre a mis un intervalle de temps pour se "déplacer selon son vecteur vitesse", alors, une seconde après le début de l'expérience, vos centres auront respectivement pour coordonnées et .

A part si les vecteurs vitesse des deux centres sont colinéaires (on traitera ce cas à part), les centres des deux cercles vont êtres amenés soit à s'approcher, puis à s'éloigner l'un de l'autre, soit à seulement s'éloigner l'un de l'autre. Dans tous les cas, la distance entre les deux centres varie et possède un minimum, appelons-le . (*)

Ce qu'on veut, c'est trouver ce minimum , et savoir à quel moment il est atteint. Une fois qu'on a ce minimum, on veut savoir si les cercles se sont effectivement cognés. Facile, ce sera le cas si et seulement si (la somme des rayons des deux cercles !).

Enfin, il suffira de faire une dichotomie avec une boucle while, pour essayer de trouver le moment, appelons-le , où la distance entre les deux centres sera comprise dans l'intervalle , où est la marge d'erreur, la précision, si vous voulez, de votre programme, que vous définirez vous-même.
Une fois qu'on aura ce moment où les cercles sont quasiment en train de se se rentrer dedans (on pourra quasiment jamais tomber pile poil sur le moment où ils se cognent), on calculera la médiatrice du segment reliant les deux centres, et bim, on se ramène au cas 1, comme indiqué dans mon précédent message.

Je sais pas si c'est la solution la plus rapide, mais c'est comme ça que je ferais, en tout cas.

Après, peut-être que votre application ne permet absolument pas d'effectuer ce genre d'opérations. Encore une fois, je n'ai pas encore bien saisi quelles informations nous fournit l'application, ni qu'est-ce qu'il est possible de faire avec.

En espérant avoir été clair, n'hésitez pas si vous avez des questions.

_____________

(*) La recherche de ce minimum est pour moi le passage le plus délicat du programme. C'est ici qu'interviendront les équations qui nous disent où se situent les centres des cercles en fonction du temps.

[Aenonis]

Je vous remercie pour ce message.

Je suis malheureusement dans le cas 1, chaque cercle étant indépendant l'un de l'autre. Informatiquement parlant, chaque cercle est un thread qui a une boucle while qui teste à chaque intervalle de temps () s'il est en collision avec son compagnon. Effectivement, le problème que vous avez soulevé apparait et un terrible manque de précision est apparent.

Avez-vous des idées pour transformer le cas 2 en application informatique ?

J'ai l'impression que toute l'application est à refaire. Refaire toute l'analyse du programme.

J'ai plus ou moins compris le concept mathématique qui se cache derrière le cas 2 mais je ne parviens pas à modéliser...

Au plaisir,

Aenonis

[Teddy-mension]

Je suis malheureusement dans le cas 1, chaque cercle étant indépendant l'un de l'autre. Informatiquement parlant, chaque cercle est un thread qui a une boucle while qui teste à chaque intervalle de temps () s'il est en collision avec son compagnon. Effectivement, le problème que vous avez soulevé apparait et un terrible manque de précision est apparent.

Oui, et même si l'on diminue , le problème n'est toujours pas résolu.

Avez-vous des idées pour transformer le cas 2 en application informatique ?

Je suis loin d'être un expert en programmation, mais je peux essayer. Je ne sais pas quel langage informatique vous utilisez, mais personnellement, on m'a tout appris sur Pyhton, et je n'sais faire que ça..

Je vous mets donc en pièce jointe un essai de programme qui aboutit au temps pour lequel les cercles se percutent.
Je suis conscient qu'il n'est peut-être pas du tout optimisé (je pense à la double approximation pour chaque dichotomie par exemple), et que j'ai certainement commis de nombreux oublis et erreurs qu'il faut surtout ne pas hésiter à me faire remarquer, mais peut-être que cela vous aidera à avancer dans vos recherches.

Je reste à votre disposition si vous avez des questions néanmoins !

NB : Le fichier est en format .jpg, car le forum n'accepte pas les formats .py. Je pourrais vous l'envoyer en privé si vous en avez vraiment besoin.