Volume

[invitef02426d6]

Bonjour,
J'arrive pas à visualiser la situation pour cet exercice:
a/ Calculer le volume délimité par les plans:
x=0 x=6 z=0 z+4y=4 z-4y=4
b/Calculer le volume du solide D qui se trouve au dessus du cône z = x²+y² z supérieur ou égal à 0 et sous la sphère z = x²+y²+z².

Pour la a, je ne suis pas sûre mais est ce que le domaine est
0<x<6 -1<y<1 4-4y<z<4+4y puis j’intègre 1 ?

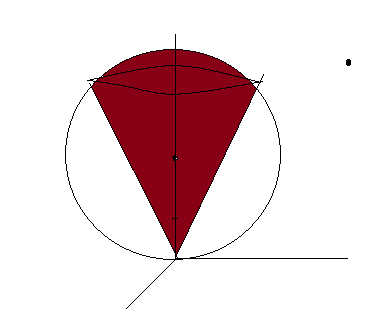
Pour la b, quand je fais le dessin j'ai bien un truc de ce genre ?
Je ne vois pas quel est le volume au dessus du cone et sous la sphère.
Merci, joyeuses fêtes !


-----

[invitef02426d6]

Pour la a, quand je projette sur YoZ j'obtiens un autre domaine, comment savoir lequel est correct ?
Merci

[inviteea16dac2]

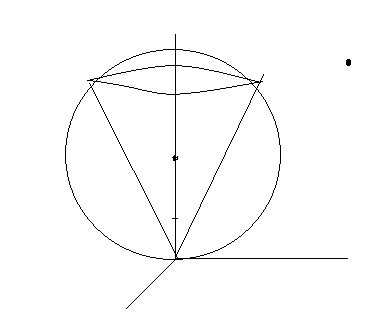
a. Les équations donnent un triangle dans le plan (y,z), l'aire de ce triangle multiplié par 6 donne le volume cherché.
b. La sphère est plus visible sous cette forme , c'est la sphère de rayon de centre . En revanche pour le cône ya un truc qui cloche : on dirait justement une cloche.

[invitef02426d6]

Bonjour,
J'avais déjà mis l'équation de la sphère sous cette forme pour la tracer. Je pense que mon cône est correct, c'est juste la partie où z est positif.
Mais où est donc ce volume qui est sous la sphère et au dessus du cône ?

[A voir en vidéo sur Futura]

[gg0]

Bonjour.

Pour le deuxième, le volume cherché est celui de l'intérieur du cône jusqu'au niveau du plan où le cône intersecte la sphère, plus la calotte sphérique située au dessus. On peut l'obtenir soit par des calculs classiques géométriques, soit comme volume de révolution engendré par la section de ce volume avec le plan Oxz (ou Oyz), soit par intégrale double de la différence entre les valeurs de z tirées des deux équations, soit par intégrale triple sur le volume entier. A toi de choisir ta méthode.

Cordialement.

[invitef02426d6]

Je dois calculer le volume de ce que j'ai colorié ?
Merci