k-Nearest Neighbors - Elements of Statistical Learning

[invite9028705a]

Bonjour,

j'ai commencé la lecture de Elements of Statistical Learning (pdf gratuitement disponible ici http://www-stat.stanford.edu/~tibs/ElemStatLearn/)

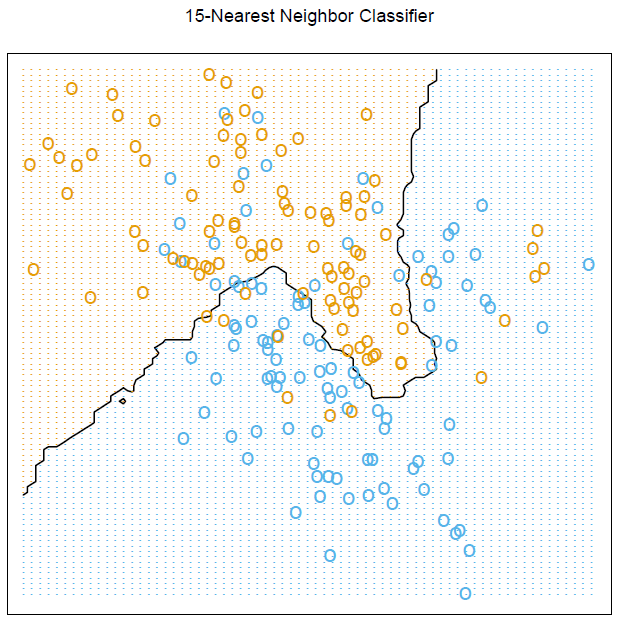
Je ne comprends pas comment est obtenu la figure de la page 15 :


Ils attribuent aux points orange la valeur 1 et aux bleu la valeur 0.
Ils calculent la moyenne des valeurs (1 ou 0 suivant la couleur) des 15 plus proches voisins (il s'agit de la méthode des k-Nearest Neighbors) pour trouver une courbe qui délimite les deux ensembles (points orange et bleu).
Apparemment ils obtiennent le graphe ci-dessus.

Je ne vois pas comment il est possible que la courbe "revienne en arrière" comme c'est le cas sur l'image (si on suit la courbe noire de la gauche vers la droite, on repart vers les x décroissants dans la dernière portion de la courbe).
Il y a donc deux ordonnées associées à une même abscisse.

Je ne vois pas comment la méthode des k-Nearest Neighbors peut aboutir à ce résultat.
-----

[Tryss]

La courbe noire n'est pas l'image d'une fonction hein.

Tu as un plan où tu as des éléments bleus et des éléments oranges, et ensuite à chaque point du plan tu attribues la couleur orange si la majorité des 15 éléments les plus proches sont oranges et bleu sinon.

La ligne noire représente juste la séparation entre la zone orange et la zone bleue.

[toothpick-charlie]

en fait pour chaque point de la grille (pointillés fins), on calcule une "probabilité d'être bleu" qui dépend du nombre de voisins bleus ou orange, et la ligne dessinée est la courbe de niveau 0.5. En faisant varier le nombre k on obtient des courbes plus ou moins lisses. Ici on voit une petite "île" orange près de la frontière. Avec un k plus petit il y aurait plus d'îles (ou lacs?). C'est une méthode de discrimination non paramétrique qui a été mise à la mode avec l'apparition du "data mining" mais dont les statisticiens savent qu'elle est difficilement reproductible (elle dépend trop des données).

[invite9028705a]

Ok merci à vous deux pour l'explication =)

Autre chose : comment est il possible de séparer linéairement les deux ensemble (orange, bleu) ?
(c'est à dire qu'on aurait une droite à la place de la courbe noire)
Je sais comment fonctionne une régression linéaire mais je ne vois pas vraiment comment obtenir une équation de droite séparant les deux classes (orange, bleu) et minimisant l'erreur.
A quel moment intervient la classe des points dans cette régression?

[A voir en vidéo sur Futura]

[toothpick-charlie]

pour cela il faut utiliser l'analyse discriminante linéaire ou une de ses généralisations (quadratique, etc)