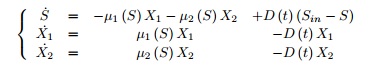Bonsoir à tous,
voila je voudrai vous poser une question assez délicate enfin pour moi...,
voila je suis en train de travailler sur un système d'équations dit du chémostat certains d'entre vous connaissent peut être en gros j'ai trois équations qui sont:
j'ai déterminé les équilibres de ce système (rien de bien compliqué il s'agit d'annuler les dérivées en S, X et Y) et j'ai trouvé comme premier équilibre (S=S_in, X_1=0,X_2=0) comme deuxième équilibre (S=S_1*, X_1=0, X_2=S_in-S_1*) ainsi que (S=S_2*,X_1=S_in-S_2*,X_2=0).
Par contre j'aimerai savoir comment étudier la stabilité d'un tel système c'est à dire la stabilité, la stabilité exponentielle, la stabilité asymptotique, la stabilité globale...
Déjà pour la stabilité j'ai étudié les différentes jacobiennes en les différents points d'équilibres et j'ai regardé leurs valeurs propres et je crois que si elles sont strictement négatives alors on peut parler de stabilité. Seulement après je ne vois pas trop comment faire pour continuer les définitions données par wikipedia me semble inexploitable cf http://fr.wikipedia.org/wiki/Stabili....A8me_autonome. En gros j'aimerai un exemple par forcément celui-ci mais qui montre comment étudier cela
Merci encore pour votre aide
-----