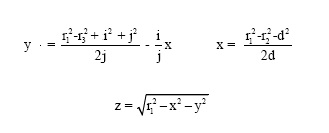trilatération

[invite2f489873]

Bonjour

Tout d'abord, un petit contexte :

Au départ, pour mon stage, on m'avait demandé de calculer les coordonnées d'un objet grâce à la trilatération à l'aide de 3 capteurs filaires.
Je connais la position de mes capteurs ainsi que leurs rayons donc j'ai pu déterminer les dimensions ijd pour pouvoir appliquer les formules et ainsi trouver les coordonées de mon objet.
Tout cela, a bien marché donc on m'a demandé autre chose.

Voici le schéma de la trilatération et les formules qui vont avec.

formule tri.jpg

trila.jpg

On m'a demandé d'effectuer le problème inverse. Je connais les coordonnées xyz de mon objet ainsi que les rayons de mes capteurs et il faut que je retrouve les dimensions ijd et par conséquent la position de mes capteurs.
J'ai pu déterminé facilement la dimension d car j'avais une équation à une inconnue donc facile.
En revanche, je n'arrive pas du tout à déterminer les dimensions i et j.

Donc j'aimerai avoir un peu de votre aide pour résoudre mon problème.
Merci.
-----

[gg0]

Bonjour.

La troisième équation ne donne rien à propos de i, j ou d, elle sert seulement de contrôle pour tes données. La première détermine d.
On a donc une seule équation (la deuxième) pour déterminer 2 valeurs. Qu'on peut réécrire :

Cette équation a généralement une infinité de solution, ou une seule, ou aucune (et c'est le cas si la dernière équation est vérifiée, c'est à dire si r₁²-x²-y²>0).

Donc soit il y a d'autres équations utilisables, soit ton problème est mal défini.

Mais surtout, tes équations 2 et 3 sont incompatibles :
La deuxième peut se réécrire
(2)
La troisième équation (s'il y a des solutions) impose
ce qui fait que l'équation (2) n'a de solution (*) que si
x=i
y=j
r₂=0
r₁= x²+y²=i²+j²
ce qui ne fait probablement pas partie des hypothèses.

Donc je soupçonne qu'il y a une erreur de copie.

Cordialement.

(*) Une somme de nombres positifs n'est nulle que si chacun des nombres est nul.

[invite2f489873]

Bonjour,

Merci pour votre réponse. Effectivement, je n'ai pas fais attention , j'ai effectivement fais une erreur de copie.
Les vrais formules sont :



Cordialement.

[gg0]

Ok.

Je ne vois plus de gros problème. Je suis un peu surpris du manque de symétrie de ces formules, mais comme je ne connais pas la trilatération ...

Par contre, on a toujours le même problème : I et j sont donnés par une formule qui ne permet pas de les calculer. Ce qui n'a rien d'étonnant à priori. De la même façon, d'un point intérieur à un terrain de football, il est facile de calculer l'angle sous lequel on voit les buts. Mais connaissant l'angle sous lequel on voit les buts, on détermine une infinité de points du terrain (en arc de cercle).

Cordialement.

NB : Si i, j et d sont les mêmes quand on intervertit les indices des capteurs, on peut fabriquer deux formules de plus.

[A voir en vidéo sur Futura]