Moindre carrés pour une surface.

[inviteb6639bce]

Bonjour à tous.

Je suis nouveau sur la forum et je vous prie de m'excuser si je me suis trompé de section pour ce post. D'autre part j'ai eu beau chercher sur le site mais je n'ai pas trouvé d'info qui réponde à mon problème :

J'ai une expérience de chimie avec un mélange d'une solution A avec une solution B pour former un électrolyte à conductivité S (qui est en fait la réponse de mon expérience).

Je cherche à connaitre les quantités de A et B (A et B variantes respectivement de 0 à 100 par exemple) pour obtenir la meilleure conductivité possible. Pour cela j'effectue plusieurs expériences et note les quantités de A et B utilisées ainsi que la conductivité du mélange obtenue correspondante dans une ligne d'un tableau. Pour obtenir la meilleure précision possible il faudrait effectuer dans l'idéal 100x100= 10 000 tests, ce qui n'est évidement pas envisageable.

J'ai d'abord tenté l'approche de Taguchi non concluante en vue du nombre de niveaux (Au minimum 10 niveaux par variables pour quelquechose de cohérent). Mais je me suis ensuite porté sur la méthode des moindres carrés.

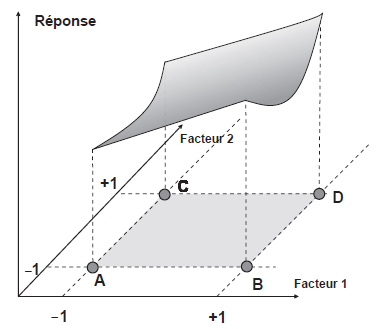
Ma question : connaissez vous un logiciel qui pourrait dessiner un graphique à réponse surfacique (3D) extrapolée aux moindres carrés grâce aux quelques dizaines de résultats d’expériences obtenus? Ou alors une fonction excel moindre carré? Je cherche en fait à connaitre le pic du graphique ci contre (A et B étant les facteurs 1 et 2 et la conductivité étant la réponse) :



En vous remerciant d'avance.
-----

[gg0]

Bonsoir.

Pour l'instant, je ne peux pas voir ta pièce jointe (" Pièces jointes en attente de validation"), mais ta phrase "Je cherche en fait à connaitre le pic du graphique ci contre" dit tout autre chose que le reste de ton message, et fait plus penser à de l'optimisation. Dans ce cas, si la conductivité ne varie pas brutalement, le "pic" sera obtenu au voisinage de la meilleure valeur obtenue (sauf si ton plan d'expériences est fait en dépit du bon sens), et une nouvelle série d'expériences pour des A et B proches donnera éventuellement une valeur plus précise.

Cordialement.

[jiherve]

bonsoir,
voir méthode de Cholesky.
Il faudra cependant avoir une vague idée de l’ordre du polynôme recherché.
JR

[inviteb6639bce]

Merci pour vos réponses.

Oui l'idée est d'utiliser une méthode d'optimisation pour trouver plus rapidement les meilleures proportions de A et B (exemple Taguchi).

gg0 : "le "pic" sera obtenu au voisinage de la meilleure valeur obtenue" C'est bien ce que je craignais...

Le graphique est une surface de réponse définie dans un repère x,y,z : X et Y correspondant à A et B dans mon cas, et Z étant la réponse.

D’ailleurs même avec Taguchi, je ne comprend pas réellement comment on peut connaitre la meilleure réponse sans l'avoir déjà testée au préalable. Tout cela reste un peu obscure pour moi...A part les tables de Taguchi qui semble être plus ou moins des tables d'extrapolation de la réponse si jai bien compris.

Merci Jherve je vais explorer cette piste.

[A voir en vidéo sur Futura]

[azizovsky]

Salut ,j'ai trouvé ça http://1.1o1.in/en/webtools/ecperimental-design , mais je ne sais pas est ce qu'il est le bon pour ton problème .

[gg0]

Deus1024,

On ne peut pas connaître la meilleure réponse, en général (impossible de tester l'infinité des valeurs possibles). mais on peut essayer de s'en approcher par divers moyens.
La méthode des plans d'expérience, avec les tables de Taguchi) suppose les variations dues aux différents facteurs indépendantes (au premier ordre), à moins d'utiliser des interactions. Les surfaces de réponse sont prismatiques, ce qui fait que la meilleure réponse est obtenue pour une certaine combinaison des facteurs. mais à priori, seules ces modalités des facteurs ont un sens.

Toi, tu sembles vouloir définir une surface de réponse. Dans ce cas, il te faut une modélisation de ton phénomène, qui permette de savoir de quel type est ta surface, ce qui est, dans ton cas, un problème de chimie. Ensuite, connaissant ce type, on sait très bien déterminer les paramètres pour obtenir la meilleure surface (par exemple par la méthode des moindres carrés), si le nombre de paramètres est faible par rapport au nombre de valeurs connues.

Cordialement.