dérivée partielle et inverse de dérivée partielles
Discussions similaires
-
Par invitea316b35d dans le forum Mathématiques du supérieur
Réponses: 2
Dernier message: 04/10/2010, 21h27
-
Par mc222 dans le forum Mathématiques du supérieur
Réponses: 5
Dernier message: 08/05/2010, 14h59
-
Par invite0435df5e dans le forum Mathématiques du supérieur
Réponses: 4
Dernier message: 19/04/2009, 15h52
-
Par invite8c2ea064 dans le forum Mathématiques du supérieur
Réponses: 8
Dernier message: 11/04/2008, 11h53
-
Par Seirios dans le forum Mathématiques du supérieur
Réponses: 6
Dernier message: 18/04/2007, 18h49




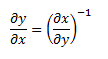
 , alors
, alors 