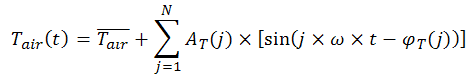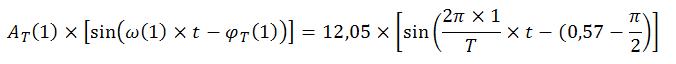Transformer une série de donnée en série de Fourier

[yoyo71]

Bonjour,

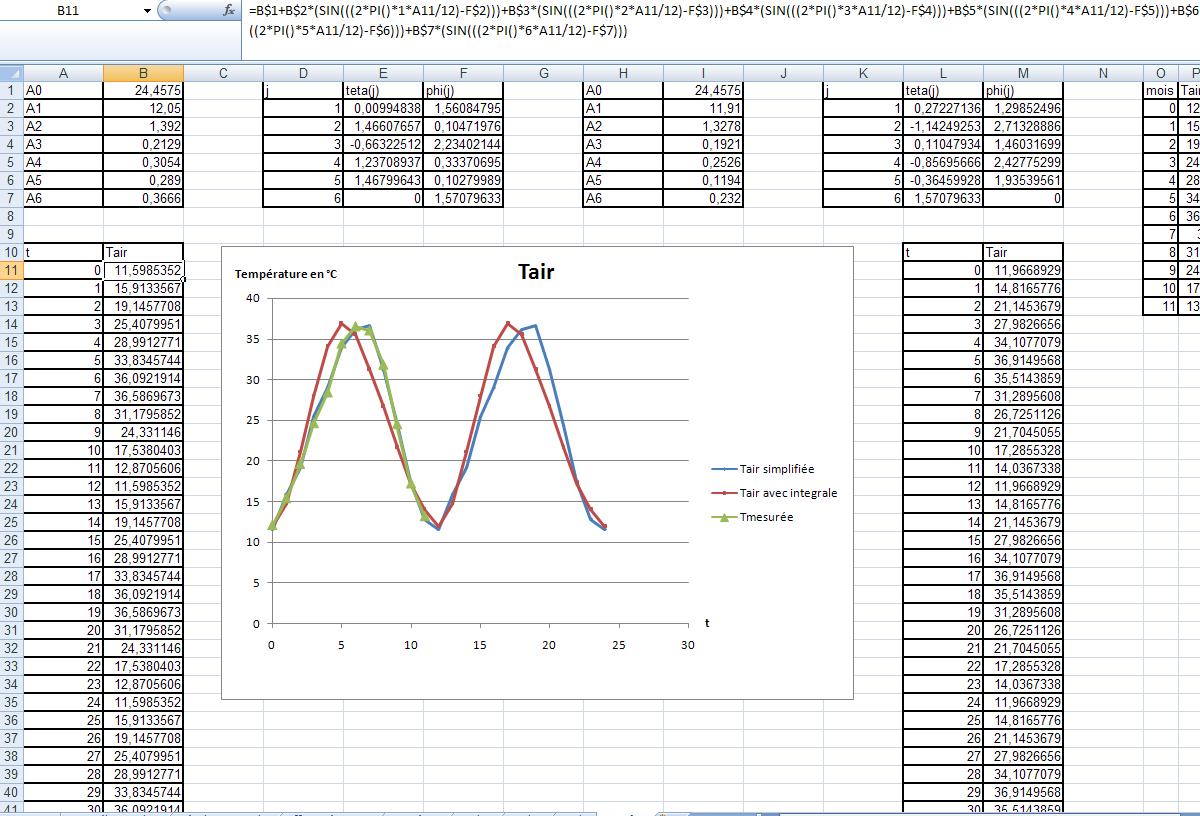
Je souhaite transformée la série ci-dessous en série de Fourier:
mois de l'année 1 2 3 4 5 6 7 8 9 10 11 12
Tair en °C 12,1 15,4 19,6 24,6 28,4 34,4 36,5 36 31,8 24,5 17,2 13,2

Je souhaite obtenir une série de Fourier sous la forme suivante:


J'aurais donc besoin de votre aide afin d'obtenir une méthode pour trouver cette série de Fourier.

La valeur moyenne de ces 12 températures est égale à 24,475 et correspond donc à T_air moyen dans l'équation.
Cependant, je n'arrive pas à obtenir le coefficient A_T ni l'angle.
Je suppose que je m'y prend mal: j'ai commencé par trouver une interpolation de la fonction et j'ai trouvé: f'(x)= 0,00392157x5 - 0,10835861x4 + 0,95798625x3 - 3,31639972x2 + 8,36508210x + 6,13181818.
En prenant cette interpolation, je trouve T_air=25,58 (je suis donc assez proche de 24,47) mais je n'arrive pas à trouve les autres coefficients.

Je vous remeercie d'avance pour votre aide.
-----

[untruc]

j'attendrais que la photo apparaisse, car je suis totalement surpris par l'utilisation du mot "série de Fourier".

Normalement si on a un signal continu périodique, on calcule une Série de Fourier.

Pour un signal discret, fini, ce qui est ton cas, on calcule une Transformée de Fourier Discrète. cf http://fr.wikipedia.org/wiki/Transfo..._discr%C3%A8te

[yoyo71]

Tout d'abord, je te remercie de ta réponse mais c'est bien une série de Fourier que je veux (enfin si j'ai bien compris).

Voici le lien du document avec lequel je travaille. Je recherche à reproduire ce qui a été fait pour la température du sol afin de le retranscrire par la suite pour un autre lieu.

http://www.cder.dz/download/Art14-2_4.pdf

Je te remercie d'avance pour ton aide

[untruc]

N ici vaut 11.
Si tu dis que 1 année correspond à t augmentant de 1, alors Omega= 2Pi
Si tu developpes le terme sin ( jwt- Phi)
tu te retrouve
A_j cos(Phi_j) sin (jwt) - A_j sin(Phi_j) cos(jwt)
A_j cos(Phi_j -pi/2) cos(jwt) - A_j sin(Phi_j -Pi/2) sin (jwt)

c'est la partie réelle de
A_j exp( i (Phi_j -Pi/2)) exp(jwt)

la formule des transformée de fourier discrètes, te donne l'expression de ce A_j exp( i (Phi_j -Pi/2))
A_j exp( i (Phi_j -Pi/2)) = 1/12 \sum_k t_k exp(-i 2Pi j k/12)
la somme allant de k=1 à 12,

Tu noteras que la formule précedente est valable pour j =1 à 11, et j=0.
Pour j=0 j'ai:
A_0 exp( i (Phi_0-Pi/2)) = 1/12 \sum_k t_k exp(-i 2Pi 0 k/12) = 1/12 \sum_k t_k = moyenne des températures (et c'est un réel)
donc tu retourve
A_0 = température moyennes
Phi_0 = Pi/2

et en effet A_0 sin( 0 w t - Pi/2) = A_0 = T_moyen


revoit calmement la TFD, ca sera plus clair,.

[A voir en vidéo sur Futura]

[untruc]

Il est probable que je me mêle les pinceaux avec les formules TFD, et TFD inverses.
Je vais regarder l'article.

[untruc]

j;ai compris. Donc lui au début de l'article, il fait une serie de fourier, d'un signal continu (qui est ici la température)

donc il a la formule du coefficient de fourier classique:
c_n(f)= 1/T \int f(u)\exp(-i 2 Pi u/ T ) du
l'intégrale allant de 0 à T.
quand on réarrange ca, dans l'esprit de ce que j ai dit plus haut. tu trouves, ton A_j et la phase.

A la fin de l'article, il un problème concret. Sont signal est discret. Il enregistre tous les mois.
mais au lieu de dire qu'il fait un TFD, il etend son signal par paliers de largeur T/12, [ et non pas par des fonctions affines comme tu as fais].
et ajuste le calcul de c_n(f)

Normalement, tu dois retrouver des formules similaires à la TFD.

C'est difficile d'ecrire sur ordi, sans faire des erreurs. Désolé.

[yoyo71]

c'est gentil de passer du temps sur mon problème.

Dis moi ce que tu as compris quand tu auras lu l'article, je poursuis mes test afin de voir ce qui cloche.

[yoyo71]

Pas de soucis pour les erreurs.

Je t'avoue que je ne comprends pas tout la.

Donc concrètement, à partir de mes 12 relevés de températures, comment puis-je obtenir la série de Fourier sous la forme donnée dans le premier post?
Car j'ai besoin de cette forme ainsi que de celle de G afin de pouvoir faire le calcul de celle de Tsol non?

[untruc]

1-définit la fonction comme fonction périodique par paliers.
2-Calcule les coefficients de serie de fourier complexes. c_n(f).
ceci doit etre bien plus simple que calculer celui d'une fonction affine. Tu dois integrer une exponentielle sur chaque palier.
3-écris la formule d'inversion des Series de Fourier dans ce cas, pour une somme allant sur les N premiers termes (les N permières harmoniques). aussi connue sous le nom de noyau de Dirichlet
f(t)= \sum_{n=-N}^N c_n(f) exp(2 Pi i n t/T)
5-maintenant tu écris que le signal est Reel, c_n(f) et c_{-n}(f) sont conjuguées.
donc il me reste c_0, et la somme de 2 Partie réelle c_n(f) exp(2 Pi i n t/T)
6-le premier coefficient c_0(f) te donne T_moyenne
7- si tu arrives à écrire la c_j(f) sous la forme A_j \exp( -i Phi_j -i Pi/2), ou A_j= module de c_j
alors la partie réelle de c_j(f) exp(2Pi i j t/T)
te donne sin(2 Pi n t /T - Phi_j)

conclusion toute la difficulté est de calculer c_n(f) en complexe.
c_n(f) = 1/T \int_0^T f(u) \exp(-2i Pi n u/T) du
c_n(f) = \sum_j \int_[jT/12, (j+1)T/12] f_j \exp(-2i Pi n u/T) du/T
= \sum_j f_j / T [ (-T/ 2i Pi n) \exp(-2i Pi n u/T) ]__[u=jT/12, u=(j+1)T/12]
= \sum_j i f_j /( 2 Pi n) [ \exp(-2i Pi n (j+1)T/12 /T) - \exp(-2i Pi n (j)T/12 /T) ]
= {\sum_j f_j \exp(-2i Pi n j /12) } i [ \exp(-2i Pi n/12) - 1 ]/( 2 Pi n)

Le terme entre {} est ce que l'on appelle une TFD du vecteur (f_0 , ... f_11) des températures.


PS:je ne m'attendais pas à trouver [ \exp(-2i Pi n/12) - 1 ]/( 2 Pi n), mais quelque chose du genre 1/12... Donc faut faire les chose proprement. Une personne plus costaud en traitement du signal peut aider.

Autre point, comme tu échantillonne à raison de 1 enregistrement tous les mois, donc 12 enregistrements sur 1 période.
Delta= ecart entre 2 échantillons = T/12
Ceci signifie que tu es en train de négliger les harmoniques de frequences au dela de 6/T.
Ca sa vient de Shanon Nyquist. Donc ton N, n'a probablement pas besoin d'etre plus grand que 6, pour te donner les résultats.

Donc si tu implémentes le calcul sur matlab ou quelque chose similaire, prendre les 6 premières harmoniques suffira. Vérifie ce point.

[yoyo71]

Je te remercie de ton explication, le problème est maintenant beaucoup plus clair à mes yeux et je cerne beaucoup mieux la méthode.

Cependant, il me reste quelques incompréhensions ^^

Tout d'abord, pour calculer les C_n(f), j'utilise la formule que tu m'as donné et que j'ai également analysé sur des cours à propos de Fourier:
C_n (f)=1/T ∫_0^T〖f(t) e^(-i 2pi n t/T) dt〗
Mais du coup pour faire le calcul et trouver les C_n, il me faut f(t) et je vois pas à quoi est égale cette fonction. J'ai un peu du mal à comprendre comment la définir par pallier périodique. Ensuite, la période T est égale à 11 ou 12?

Ensuite, dans ton détail du calcul de C_n (f), je n'arrive pas à bien identifier les formules que tu as mises et donc de les comprendre


Pour le nombre d'harmoniques, je suis d'accord avec toi.

Encore merci de me consacrer du temps et de me permettre de comprendre ce problème.

[yoyo71]

Pour le C₀ le calcul est donc le suivant:
C₀(f) = 1/T ∫_0^T〖f(t) e^(-i 2pi n t/T) dt〗= 1/T ∫_0^T〖f(t) dt〗qui est donc égale à ma valeur moyenne de mes températures
(je vérifierais avec la fonction f(t) quand tu m'auras éclairer à quoi elle est égale et avec la bonne période T)
et du coup, le C₀(f) correspond au A₀ qui est égal au T_air moyen de la formule que je cherche à obtenir.

Après, si j'ai bien compris le raisonnement, je dois calculer c1, c2, c3,... c6 (pour obtenir mes 6 harmoniques)

[untruc]

comme j'ai précisé dans le calcul de c_n(f), prends une fonction affine par paliers.

La péiode va dépendre de ce que tu considère etre t=1 an.
Par exemple, si pour toi 1 an <=> t=1, alors ta période est 1.
et 1 mois de plus représente 1/12.

Du coup, f(t)= f_j quand
ou f_j température au mois j

tu vois directement que

pareil pour c_n, sauf que cette fois

donc

d ou

le terme intégrale est une intégrale d exp, que l'on sait calculer très facilement.

pas la peine de s'embrouiller avec des interpolation affines de f.

[untruc]

on peut se simplifier la vie et faire une approximation grossière, meme pas besoin de calculer

ecrit simplemeent que c'est à peu près egal à [ou aussi ]

du coup



ca c'est la transformée de fourier discrète du vecteur f_j.

normalement dans matlab, tu donnes un vecteur de 13 ponts, la commende fft, te retourne sa transformée de fourier discrète, qu'il ordonne ainsi:
[c_0, c_1, .... c_6. c_{-6}, c_{-5} , ... c_{-1}]
il a une autre fonction fftshit, qui les remet dans l ordre de -6 à 6.

[yoyo71]

Merci pour ton aide,

je regarde ça tout à l'heure et je te redis ce que j'ai trouvé

[yoyo71]

Salut,

Dsl de répondre que maintenant mais je n'ai pas pu avancé ce week-end.

J'ai donc calculer les différents Cn avec la méthode simplifiée et la méthode composée de l'intégrale.
Avec la méthode simplifiée, j'ai obtenu:
c0= 24,475;c1= -6,0250+0,0638i;c2= 0,0667-0,6928i; c3= -0,0833-0,0667i; c4= -0,0500+0,1443i;c5= 0,0083-0.0805i; c6= -0,1833+0i;
c-1= -6,0250-0,0638i;c-2= 0,0667+0,6928i;c-3= -0,0833+0,0667i;c-4= -0,0500-0,1443i;c-5= 0,0083+0.0805i;c-6= -0,1833-0i;
exemple de calcul pour C1: equation1.JPG

Avec la méthode par intégrale, j'ai:
c0=24,475;c1= -5.7371+1,6026i; c2= -0,2757-0,3040i; c3= -0,0955 + 0,0106i;c4= 0,0827+0,0955i; c5=-0,0558-0,0213i; c6= 0,1167i;
c-1= -5.7371-1,6026i;c-2= -0,2757+0,3040i;c-3= -0,0955 - 0,0106i;c-4= 0,0827-0,0955i;c-5=-0,0558+0,0213i;c-6= -0,1167i;
exemple de calcul: equation2.JPG

Ensuite, si j'ai bien compris, je peux calculer an et bn avec: a_n=c_n -c_-n et b_n= j(c_n - c_-n)
Je peux alors obtenir A_T(j)=racinecarre(a_n^2+ b_n^2)

Pour l'angle phi_T(j), j'ai regardé la formule du noyau de Dirichlet comme tu me l'as indiqué mais je ne comprends pas comment tirer l'angle de cette formule

Merci de ta patience et de ton aide car je galère un peu

[yoyo71]

J'ai par exemple a₁=-12,05 et b₁=-0,1276
Ce qui me donne A_T(j=1)=12,05

J'ai fait de même pour les autres

[untruc]

on a dis plus haut qu'il faut mettre c_j sous la forme
A_j \exp( -i Phi_j -i Pi/2)
alors la partie réelle d terme 2 Re( c_j(f) exp(2Pi i j t/T) ) qui vient de la formule de Dirichlet.

va te donner:
sin(2 Pi n t /T - Phi_j)

donc Phi est lié à l'argument complexe de c_j, par une formule à vérifier: \theta_j = - Phi_j - Pi/2.

tu n'ecris pas les a_n et les b_n. tu calcules directement module et argument de c_j, et tu sors ce Phi_j.
accessoirement, si tu as tes a_n, b_n, l'argument de c_j sors de arctan(bn/an), auquel tu dois probablement

ou aussi, tu prends chaque expression a_n cos (...) + b_n sin (...) =A_j [a_j/A_j cos (...) + b_j/A_j sin (...)] et tu linéarises. pour remettre sous la forme sin( ...)

PS: calculer une matrice 6x6 est faisable, mais lourd. Si tu n'as pas matlab, utilise scilab.

[yoyo71]

Je suis passé par les a_n et b_n car c'est simple de les trouver à partir du c_n.
Et il est facile de calculer l'argument qui est égal à artan (b_n/a_n). Cependant cet argument n'est pas égale à Phi_n si j'ai bien compris le raisonnement. Or je ne vois pas comment trouver phi_n à partir de cet argument. (dsl je patauge un peu la)

Tu m'as donné ça :theta_j = - Phi_j - Pi/2 ce qui me donnerait : Phi_j= -theta_j - Pi/2
Par conséquent, si j'obtient mes theta_j en fonction de mes a_n et b_n
J'ai alors directement mon phi_j.

En résumé j'aurais par exemple:
-pour c1= -6,0250+0,0638i => a1=-12,05 et b1=-0.1276 => theta₁=arctan(b1/a1)=0,57 et A1=12,05
J'ai alors phi₁=0,57- pi/2
Pour finir, j'obtiendrais:


Je fais de même pour c2 à c6

Mais je ne suis pas sur que mon raisonnement soit bon et donc que je sois obligé de passer par la formule de Dirichlet?

[untruc]

la fomrule de dirichlet c'est celle qui lie le signal s à sa serie fourier, donc avec avec les an bn , ou les cn.

ton article, veux réecrire cette somme en linérarisant les élements a_n cos + b_n sin, sous une forme particulière A_j sin ( .... - Phase)

l’écriture finale qu il veut, impose de prendre une relation un peu tordue entre argument de c_n et Phase.

maintenant, tu dois tracer la courbe que tu obtiens avec les 6 premier termes de la forme A_j sin ( ... - phase)

normalement tu dois trouver une courbe qui est proche de ta courbe des températures ( cette courbe est la même que celle de la formule de Dirichlet pour les 6 premières harmoniques)

[yoyo71]

Ok merci, je vais essayer de tracé ça demain en espérant que ça marche

[yoyo71]

Salut, je viens de tracer la courbe mais j'obtiens des choses un peu étrange (j'ai surement dût faire une erreur)

En effet, j'obtient une allure plutôt correcte mais avec une échelle de temps incorrecte.
De plus, on peut observer un problème de déphasage.
courbe1.JPG
Dans la formule, je multiplie mes angles par PI()/180 afin de convertir en radian car les sinus et cos sont utilises en radian dans Excel.
Pour la période T, j'ai essayé de mettre 12 pour voir mais cela ne change rien pratiquement.
Pour PHI, j'ai bien fait phi=-teta-90 (phi=-teta-PI/2).

J'ai alors essayé de changer l'angle phi en mettant phi=-teta+90 et j'obtient alors une courbe plus logique au point de vue phase:
courbe2.JPG

Pour finir, en gardant l'angle phi tel que: phi=-teta+90 et en supprimant les (*PI()/180) dans la formule, j'obtiens une courbe très proche de la courbe de température pour la méthode simplifiée et un courbe déphasée pour celle avec intégrale.
courbe3.JPG


Par hasard, aurais-tu une idée de l'erreur que j'aurais commise car du coup il y a quelque chose qui cloche. En effet, ce n'est pas logique de supprimer les (*PI()/180).

Je te remercie d'avance pour ton aide.

Je vais essayer de faire la même chose avec G puis tester avec d'autres valeurs pour voir.

PS: encore merci pour tout le temps que tu me consacres

[untruc]

donc il y avait une erreur de signe sur la relation phi_j avec argument de c_j, probablement dépend de la forme finale sous laquelle tu voulais réduire ta formule de Dirichlet: sin( ... - phase) ou sin( ... + phase).

Par ailleurs, les sin et cos ont toujours été en radian.
La relation sin'(0)=1, n'est valable que si sin est le sin d'expressions en RADIAN. les relations de dérivées sin<-> cos ne sont valable que si on travaille en radian.
Les sin et cos dans toutes les formules de fourier sont donc en radian.
On ne multiplie jamais par Pi/180.

[yoyo71]

Ah oui, pas bête pour les radians, petite erreur d’inattention de part.
Mes angles teta étant en degré, il faut que je corrige ça de suite.

l'erreur doit surement venir de la

[polf]

N'oublies pas d'ajouter 0.2°C par an pour le réchauffement climatique

[yoyo71]

Après correction de mes angles, je trouve bien une courbe proche de celle de la température:

Par contre, est-ce normal que la méthode simplifiée soit plus proche que celle avec les intégrale?

Maintenant, je dois faire de même pour G avec la même méthode, je n'ai rien à changer?
car je trouve des amplitudes immenses (je me suis peut-être trompé dans mes calculs)


@polf, merci pour l'idée, je vais essayer d'intégrer ce genre de chose après

[yoyo71]

Oups, j'ai juste oublier mon 1/12 dans mes calculs ça a l'air mieux.

Il me reste plus qu'à voir mon Tsol

[untruc]

tu peux croire que la méthode avec les cn exprimées sous forme intégrales, et f interpolée affine, est plus précise.

La réalité, est que tu n'as introduit aucune information réelle dans tes données. Tu as toujours tes misérables 12 relevés de température. Pour cette raison, l'approximation est acceptable

[yoyo71]

Merci pour ton éclaircissement à propos de la précision entre les 2 méthodes.

J'ai pu grâce à toi comprendre la méthode afin de trouver Tsol même si je t'avoue que pour l'instant, je n'ai pas encore les bonnes valeurs mais niveau forme de la courbe, je suis plutôt pas mal.

Cependant, je me demandais si cela était normal que je sois assez éloigné de la courbe de G?
courbe5.JPG
Je pense que cela vient du fait que l'écart entre les 12 valeurs soit plus importante et entraîne donc des un série moins précise.

Je me demandais aussi par hasard, si tu penses qu'il est mieux de réaliser Tair en Kelvin afin de trouver Tsol ou non car actuellement je trouve une température du sol qui ne varie très peu et je pense que cela peut venir de ça.
sol.JPG

[untruc]

déjà tu as 11 valeurs de températures par an, au lieu de 12.

si tu donne donnes 12 valeurs, et tu fais une tfd, puis tu fais une tfd inverse, tu dois retomber sur les memes valeurs initiales.
intuitivement la fonction que tu obtiens, celle des sum c_n(f), aurra tendance à interpoler ta fonction.

ta fonction est super lisse, les 12 points suffisent. Le décalage peut venir de manière dont tu définis la température.

Si tu veux absolument continuer à utiliser excel, trouves toi un module qui fait des series de fourrier, et des transformées de fourier discretes, et rajoute le à cet excel.

[yoyo71]

La j'ai utilisé Excel car je l'avais sous la main et que ça me permettait ainsi de voir le résultat directement.
Je regarde ça sur Matlab ce soir. Sur Matlab, je dois juste rentrer mon vecteur avec mes 12 temperatures et utiliser la commande afin de réaliser la TFD?


Quand tu me dis que le décalage peut venir de la manière dont je définis mes températures, je vois pas trop ce que tu veux dire.