Nombre de phrases aléatoires selon un tableau prédéfini (calcul)

[Backeljau]

Voici ma question, je sais, elle est élémentaire, mais pas pour moi.
Imaginons une phrase découpée en sections dans autant de colonnes d’un tableau ;
chaque colonne comporte des expressions synonymes ;
chacune des lignes sera donc un énoncé différent ;
mais il sera aussi possible de lire dans chaque colonne une ligne aléatoire ;
on obtient ainsi un très grand nombre d’énoncés.

Comment calculer ce nombre, compte tenu que les colonnes ne peuvent permuter, seules les expressions dans chaque colonne sont choisies au hasard.

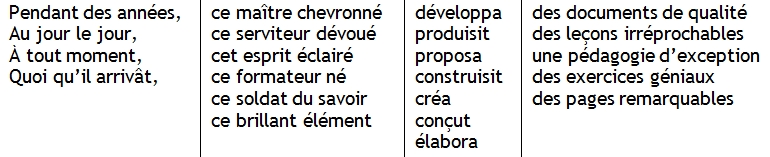
Voici un exemple concret : quatre sections, de quatre à sept expressions par section.
Selon moi, le nombre d’énoncés serait de 840 : [(4 × 6 = 24) × 7 = 168] × 5 = 840.
Mon raisonnement est-il exact ?
Sinon, n'ayant pas de compétences mathématiques, puis-je espérer une aide ?


-----

[minushabens]

Ton calcul est bon, il faut faire le produit des nombres de choix pour chaque élément.

[Backeljau]

Ton calcul est bon, il faut faire le produit des nombres de choix pour chaque élément.

Je vous remercie de votre réponse et de sa rapidité.
J’ai mis en ligne sur mon site un générateur de phrases. La phrase est divisée en neuf sections, chaque section comprenant deux à huit formulations, pour un total de formulations de 48.
Selon mes calculs, ce tableau génère 1 814 400 énoncés. Ce serait donc bien le cas ?

[Backeljau]

minushabens, je ne vous demandais pas un calcul comptable mais un ordre de grandeur.
En effet, j'ai mal formulé la question, puisque je ne donnais pas le nombre d'expression précis dans chaque colonne.
Voici le tableau en pièce jointe.

[A voir en vidéo sur Futura]

[Bluedeep]

On notera que tous les "pipotrons" sont faits plus ou moins sur ce modèle.

[Backeljau]

On notera que tous les "pipotrons" sont faits plus ou moins sur ce modèle.

Je redoute une ombre d’ironie derrière cette sentence mais la référence est pertinente. Une recherche sur la toile renvoie à quelques sites dévoilant la mécanique : outre l’affichage de l’énoncé aléatoire apparaissent généralement sous forme de tableaux les listes des choix où sont surlignées les occurrences actuelles. Bien.
L’intervention de Bluedeep ne répond pas à ma question : mon « Satisfecit-o-tron » génère-t-il près de deux millions d’énoncés ?
Cependant, le site http://www.pipotron.free.fr/ précise dans sa colonne droite : « Actuellement le pipotron génère 121 247 280 000 formules différentes. Le pipotron est une invention originale de Yves, qui a bien voulu nous donner l'autorisation de l'adapter. » La phrase est divisée en neuf sections, comportant de huit à vingt expressions : l’ordre de grandeur des énoncés générés semble donc confirmé et le mode de calcul pour les dénombrer aussi.

[Médiat]

Bonjour,

La source du concept par Raymond Queneau (1961) : http://fr.wikipedia.org/wiki/Cent_mi...de_po%C3%A8mes

[Backeljau]

La source du concept par Raymond Queneau (1961) : http://fr.wikipedia.org/wiki/Cent_mi...de_po%C3%A8mes

Je vous remercie pour cette référence. Je complète d'ailleurs la page de mon site à ce sujet.

[Bluedeep]

Je redoute une ombre d’ironie derrière cette sentence .

Absolument aucune; c'était une constatation, c'est tout.

mon « Satisfecit-o-tron » génère-t-il près de deux millions d’énoncés ?

Oui, sans le moindre doute.

[Bluedeep]

Un dernier point : ne pas oublier qu'en français, il est nécessaire d'avoir un mécanisme d'ajustement syntaxique pour régler la question des apostrophes dans certains cas, la simple concaténation aléatoire pouvant ne pas fournir de résultats corrects. (même si le problème ne se pose pas avec l’exemple fourni supra)

[Backeljau]

Un dernier point : ne pas oublier qu'en français, il est nécessaire d'avoir un mécanisme d'ajustement syntaxique pour régler la question des apostrophes dans certains cas, la simple concaténation aléatoire pouvant ne pas fournir de résultats corrects. (même si le problème ne se pose pas avec l’exemple fourni supra)

En effet, vous soulevez un point important. Le code source du site http://www.pipotron.free.fr/ montre la solution avec le bécarre (chaîne 4). Je n'allais pas si loin.
Je vous remercie d'avoir étendu vos remarques au champ littéraire, même si ma préoccupation était purement mathématique. L'ouvrage de Queneau cité ici aurait dû m'orienter mais mieux vaut une certitude plutôt que de publier une bourde.

[Backeljau]

Oui, sans le moindre doute.

C'était exactement ce que je voulais savoir. Merci.

[Backeljau]

« Cours toujours » ayant un domaine propre de puis juillet 2021, le lien pour atteindre le générateur de phrases est le suivant : satisfecitotron.htm.

[Backeljau]

Bonjour,
En mars 2022, la page est rangée dans un dossier renommé, elle se consulte avec ce lien :
https://courstoujours.be/annexes/cah...fecitotron.htm.
Bonne visite !

[Backeljau]

Bonjour à toutes et à tous,
Le lien a changé, vous le trouvez désormais ici : https://courstoujours.be/cahier/satisfecitotronBis.htm
Bonne visite !