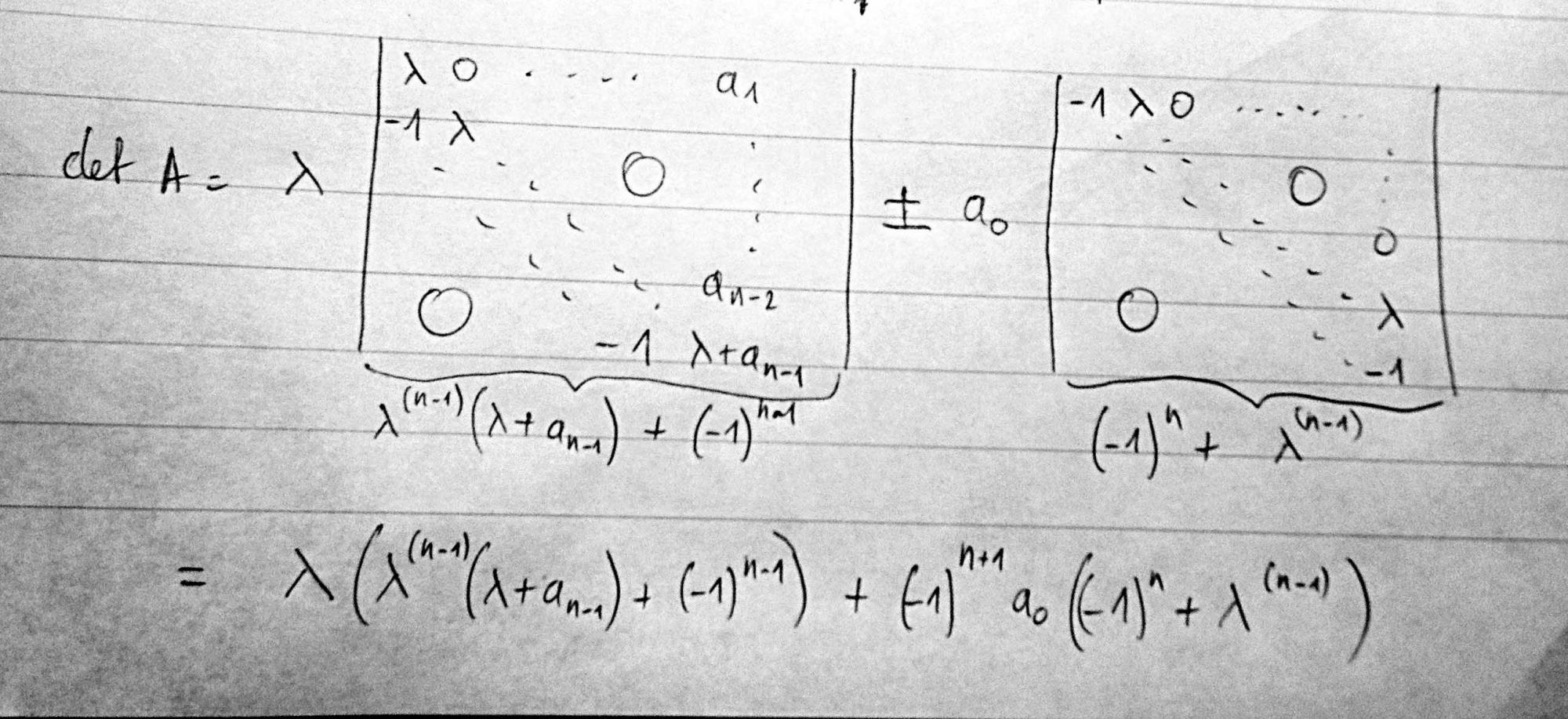Bonjour,
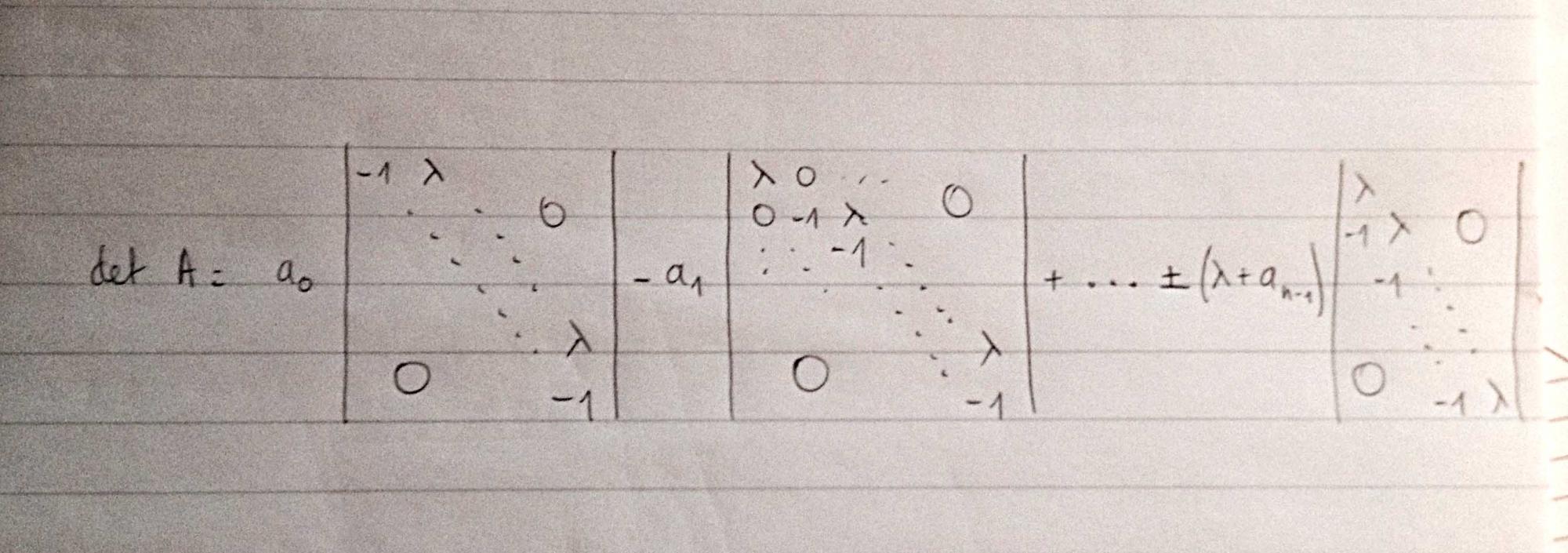
Je dois calculer le déterminant de la matrice nxn ci-jointe pour un devoir, mais je ne sais pas comment m'y prendre. Chaque méthode que j'utilise me donne des résultats différents! Quelqu'un peut-il me donner un indice sur la méthode à suivre s'il vous plaît? À préciser que tous les éléments de la matrice qui ne sont pas indiqués sont 0.
En vous remerciant d'avance,
Julien.
Au passage voici la dernière solution que j'ai trouvé. Pas vraiment convaincu...
Le plus simple est de développer sur la dernière colonne, et de constater que le déterminant mineur associé à chaque ai est une matrice, avec un certain nombre de lambda et un certain nombre (pair ou impair) de -1 dans la diagonale, qui va permettre de compenser les (-1)^i venant de la formule, et une ligne/colonne qui ne contient qu'un élément non nul.
Au total vous allez trouver un polynome en lambda de degré n, dont le coefficient de degré n vaut 1, celui de degré n-1 an-1...
Je vous laisse deviner la suite...
Dernière modification par Resartus ; 08/01/2016 à 20h16.
Sinon, votre méthode en développant sur la 1ere ligne peut marcher aussi, par récurrence, à condition de ne pas se tromper. Sur la matrice associée à a0 seuls comptent les -1 sur la diagonale,elle vaut donc (-1)^(n-1), ce qui compense le signe dans le calcul du mineur.
Quant à la première matrice multipliée par lambda, on retrouve une formule semblable à celle à trouver, mais avec maintenant seulement n-1, et avec a1 an-1 en dernière colonne. On peut ainsi par récurrence écrire
Dn=a0+lambda*Dn-1=a0+Lambda*(a1+Lambda*Dn-2)=a0+a1*lambda+lambda*(a2+lam bda*(Dn-3)=....
Bonjour, et tout d'abord merci pour votre réponse.
Ah bon? Je ne comprends pas pourquoi les lambda sont à ignorer?Sur la matrice associée à a0 seuls comptent les -1 sur la diagonale
Quant à votre première méthode, si je l'ai bien compris, voici l'étape suivante (voir image attachée). Est-ce que cela est correct?
Cordialement.
Julien.
Comme vous l'avez bien représenté, en ayant retiré la première ligne et la dernière colonne, les -1 sont maintenant dans la diagonale et tous les termes au dessous sont nuls. C'est donc une matrice triangulaire supérieure, dont seule la diagonale fournira un terme non nul...
Dernière modification par Resartus ; 08/01/2016 à 22h18.
