Un lemme de Chasles

[invitebc19a927]

Bonjour,
J'ai trouvé quelque part ce joli théorème, attribué à Michel Chasles, utile pour démontrer de manière expéditive, si je me souviens bien, le théorème de l'hexagramme mystique.

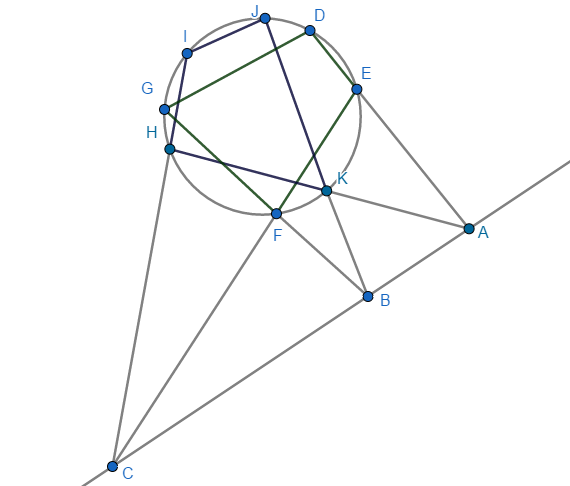
Deux quadrilatères ABCD et A'B'C'D' sont inscrits dans un même cercle. On peut former trois couples de côtés appartenant respectivement aux deux quadrilatères (par exemple (AB) et (A'B')), concourant en trois points alignés.
Montrer que le dernier couple de côtés est concourant en un point situé sur la même droite.

Chasles devait trouver cela évident et il n'employait ni l'inversion ni la géométrie projective, inventées un peu plus tard. Sans doute une conséquence d'un théorème de Desargues ? Je sèche...
-----

[invite9dc7b526]

Ca m'a l'air faux: prends pour ABCD et A'B'C'D' deux carrés décalés d'un huitième de tour. Les 8 points d'intersection de deux côtés de carrés différents forment un octogone régulier et il n'y a pas trois points alignés.

[invite51d17075]

effectivement.
as tu un lien sur ce "théorème".
car par ailleurs, cela n'est pas en rapport avec l'hexagramme mystique.
https://ljk.imag.fr/membres/Bernard.Ycart/mel/co/node20.html

[invitebc19a927]

Je me suis sans doute mal exprimé. On a, inscrits dans un même cercle, deux quadrilatères TELS que trois couples de côtés homologues sont concourants en trois points alignés. C'est l'hypothèse.
Et le théorème dit que dans ce cas, le quatrième couple de côtés homologues (IJ) et (GD) est concourant sur la même droite.ABC.

Oui, j'ai eu une source, un lien, mais là, je l'ai perdu. De toutes façons, ce lien ne donnait pas la preuve. Dans un autre théorème (peut-être du style hexagramme mystique, ou pas) Chasles fait appel à ce résultat pour une démonstration expéditive.
Merci, en tous cas, de vous intéresser à ce théorème.

[A voir en vidéo sur Futura]

[invite6710ed20]

Bonjour
Non l'énoncé est correct mais les 2 quadrilatères sont liées par le fait que les 3 premiers points sont alignés (c'est une hypothèse).
Pour la démo je pense l'avoir mais pour la donner mais il me faut faire un petit effort de rédaction, vu que j'ai pas fait de géométrie depuis longtemps. Mais grosso modo, je considère différentes perspectives sur la droite (d), perspectives issues de différents points du cercle bien choisis.
Ces perspectives conservant le birapport.
Alors en guise de révision, j'en déduis le résultat suivant:
Soit une conique K non dégénérée et 8 points distincts A,B,C,D
et E,F,G,H sur K .
On construit alors les droites de la façon suivante:
La tangente en A et en B se coupent en un point noté A*B et l'homologue du point A*B est noté E*F (il est obtenue de la même façon en remplaçant A par E et B par F).
La droite passant par A*B et E*F est notée (ABEF).
Ainsi de suite on construit ainsi en tout 4 droites
(ABEF), (BCFG), (CDGH) et (DAHC).
Alors si les trois premières sont courantes, la 4ème (DAHC) est concourante avec elles.
La aussi une figure est difficile à faire car il faut s'arranger pour que les 3 premières droites sont concourantes, on peut le faire avec Geogebra.