problème du voyageur de commerce

[Adri0]

Bonjour à tous,
J’ai une idée que je souhaiterai exprimer concernant le problème du voyageur.
N’hésiter pas à me rattraper au vol si c’est incompréhensible ou simplement si c’est nimp..

Le problème du voyageur de commerce pose comme problématique de trouver le chemin le plus court reliant plusieurs villes entre elles avec un point de départ et d’arrivée identique.
Il n’existe pas un mais deux trajets les plus courts, le premier et son exact inverse pour le second.
Le chemin est une boucle passant une fois par toutes les villes et revenant à la ville d’origine, ce qui implique que nous ne sommes pas obligé de commencer le calcul par la ville d’origine, nous pouvons commencer par n’importe quelles villes à visiter. (du moment que l-on passe une fois par toutes les villes)


Soit
Nice = N
Paris = P
Londres = L
Rome = R
Madrid =M
Berlin = B
Athènes =A

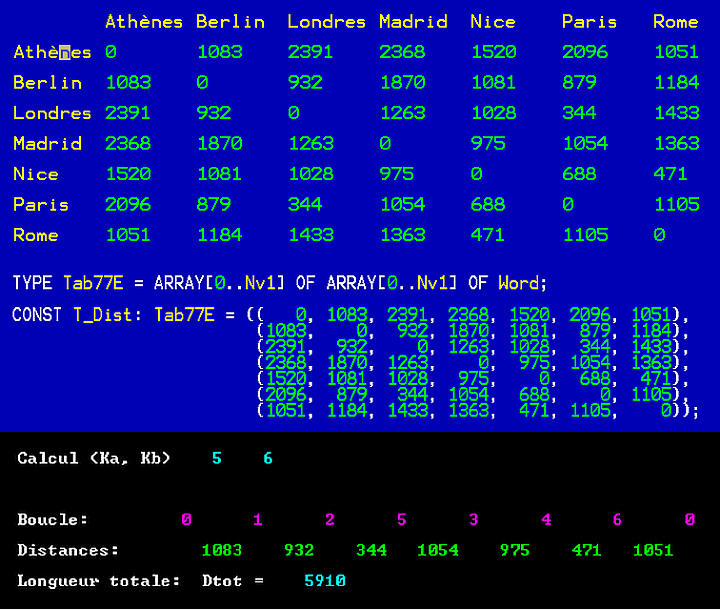
Avec 6 villes :
21 distances à mesurer :
NP = PN = 688 km
PL = LP = 344 km
LN = NL = 1.028 km
NR = RN = 471 km
PR = RP = 1 105 km
RL = LR = 1.433 km
MN = NM = 975 km
MP = PM = 1054 km
ML = LM = 1263 km
MR = RM = 1363 km
BN = NB = 1081 km
BP = PB = 879 km
BL = LB = 932 km
BR = RB = 1184 km
BM = MB = 1870 km
AN = NA = 1.520 km
AP = PA = 2.096 km
AL = LA = 2391 km
AR =RA = 1051 km
AM =MA = 2368 km
AB =BA = 1083 km

I.
faire la somme des chemins d’une ville à toutes les autres :
Dans l’exemple avec une ville d’origine et 4 villes à visiter :

Pour la ville de Nice :
Nice à Rome + Nice à Paris + Nice à Madrid + Nice à Londres = 3162km
Pour la ville de Paris :
Paris à Londres + Paris à Nice + Paris à Madrid + Paris à Rome = 3191km
Pour la ville de Londres :
Londres à Paris + Londres à Nice + Londres à Rome + Londres à Madrid = 4068km
Pour la ville de Rome :
Rome à Nice + Rome à Londres+ Rome à Madrid+ Rome à Paris = 4372km
Pour la ville de Madrid :
Madrid à paris + Madrid à Londres + Madrid à Rome +Madrid à nice = 4655km

La somme la plus petite détermine la ville de départ, il s’agit de la ville la plus centrée par rapport aux autres.
II. classer les villes par rapport aux sommes obtenues en I. , respectivement de gauche pour la plus petite à droite pour la plus grande dans un tableau.
Ici :
Tout à gauche Nice avec 3162km puis Paris avec 3191km puis Londres avec 4068km puis Rome avec 4372km puis tout à droite Madrid avec 4655km.

III.
Les chemins possibles ainsi que leurs distances sont inscrit dans les colonnes en dessous de chaque ville et par ordre croissant (le plus petit en haut).

VI.
Chercher les combinaisons les plus petites existantes, il faut « passer d’une colonne à une autre et repartir de la donnée possible la plus haute dans la colonne »

Dans l’exemple :
Nous partons de Nice vers Rome,
Une fois dans la colonne de Rome nous sélectionnons le chemin le plus court au départ de Rome (le plus haut possible dans la colonne Rome), ici départ vers Paris.
Une fois dans la colonne de Paris nous sélectionnons le chemin possible le plus court au départ de Paris(le plus haut possible dans la colonne Paris), ici vers Londres.
Dans la colonne de Londres nous sélectionnons le chemin possible le plus court, ici vers Madrid car Londres-Paris déjà fait, Londres-Nice retour impossible car toutes les villes n’ont pas été visitées.
Et retour de Madrid vers Nice.
Soit : NR + RP + PL+ LM + MN pour le chemin numero 1.


tableau calcul chemins par équilibre des distances 5 villes.png

tableau calcul chemins par équilibre des distances 6 villes.png

tableau calcul chemins par équilibre des distances 7 villes.jpg

si vous avez lu merci à vous..
-----

[gg0]

Bonjour.

Il te reste à traduire ça en un algorithme précis, puis démontrer que ça donne bien le chemin le plus court à chaque fois; et enfin calculer le temps d'exécution de ton algorithme. Si tu fais mieux que les algorithmes connus (il y en a plusieurs) tu amènes un progrès et si ton algorithme est polynomial c'est une révolution !
Le problème du voyageur de commerce, c'est ces deux derniers points.

Cordialement.

NB: rien à voir avec la logique.

[amineyasmine]

Bonjour
Tu es en train de s’attaquer au problème PNP (P vs NP), il est à un million de dollars.

Il est facile de vérifier une solution mais trouver une solution générale (algorithme) demandant un temps polynomiale n’est pas facile et on ne sait pas si cette solution existe.

On remplace les villes par les grains de sable d’une petite plage et le voyageur par un être miniature qui doit passer par toutes villes (tous les grains) et faire le chemin le plus cours.

Il faut pousser la réflexion un peu plus loin

[Deedee81]

Salut,

Pour s'attaquer au problème PNP, il me semble qu'il est plus intéressant de prendre une version la plus simple possible des problèmes NP-Complet.
Il me semble qu'au niveau théorique le plus simple pour une attaque théorique est 3-Sat : https://fr.wikipedia.org/wiki/Probl%C3%A8me_3-SAT

S'il s'agit juste de s'amuser avec un problème NP-Complet je trouve que le problème du démineur est plus sympa (à partir d'une configuration intermédiaire quelconque déterminer si cela peut correspondre à un jeu réel).

S'il s'agit juste de pondre un algorithme, pourquoi pas. Comme dit plus haut il en existe plusieurs y compris des approchés fort bons et polynomiaux (le recuit simulé par exemple). Et le voyageur de commerce a le bon goût d'être à la base de beaucoup de problèmes pratiques, parfois sous des formes modifiées (la conception de circuits intégrés ou imprimés par exemple).

Mais même dans ce cas il est indispensable de faire ce qui a été dit : démontrer (au sens mathématique rigoureux) que ça marche dans tous les cas et déterminer (au moins par des essais) sa complexité (sauf si on veut gagner le PNP, là faut le démontrer, pas juste donner des exemples).
(je n'ai lu qu'en diagonale, c'est assez touffu et confus, mais à première vue je doute que ça marche dans tous les cas, mais je peux me tromper, je n'ai pas assez creusé)

Mais d'une manière générale : ce message est mal placé, non ? Il n'a rien à voir avec https://fr.wikipedia.org/wiki/Logique_math%C3%A9matique
(ne pas confondre évidemment avec la logique au sens commun)
Il faudrait le déplacer dans le forum de math du supérieur si la question est mathématique ou dans le forum d'algorithmique s'il s'agit plutôt de programmation. Le message initial n'est pas clair sur ce point.
Je laisse Adri0 en décidé ou les modos de ce forum.

[A voir en vidéo sur Futura]

[albanxiii]

NB: rien à voir avec la logique.

Et donc déplacé en mathématiques du supérieur, faute de rubrique algorithmique et fondements de l'informatique.

[MissJenny]

Il n’existe pas un mais deux trajets les plus courts, le premier et son exact inverse pour le second.

il pourrait y en avoir plus de deux.

[danyvio]

il pourrait y en avoir plus de deux.

Tout à fait

[Deedee81]

Salut,

Si c'est une boucle (comme proposé au début du premier message) il y en a même plus de deux (en incluant le point de départ)

[Médiat]

Bonjour,

Avant de se lancer dans des démonstrations, avez-vous
1) vérifié que vos solutions pour 4, 5, 6 et villes sont optimales
2) compté le nombre de calculs à faire pour 50 ou 100 villes, n villes (si c'est possible)
3) vérifié que votre solution pour 50 ou 100 villes est optimale

[Médiat]

Voir aussi : Le problème du voyageur de commerce : le défi des 250 villes (free.fr)

[Médiat]

Personnellement, si j'ai bien compris, je doute que cela marche :

1) Choisir la ville de départ comme vous le faite, pourquoi pas, de toute façon il faut passer par toutes.
2) Choisir la 3ième ville repose sur un algorithme
3) Choisir la 2ième ville repose sur la liste exhaustive de tous les cas possibles

Autrement dit votre alorithme marcherait à partir de la troisième mais pas de la deuxième ville, c'est bizarre et même suspect.

Si j'étais vous, je testerais sur le défi des 250 villes pour voir où vous vous placez en distance et en temps

[Deedee81]

Si j'étais vous, je testerais sur le défi des 250 villes pour voir où vous vous placez en distance et en temps

Le mieux serait déjà qu'il le programme (c'est quand même pas difficile d'écrire un programme) et le teste sur disons 4 villes
(d'abord pour voir s'il sort quelque chose de cohérent, puis après seulement s'il donne bien le plus court et enfin après sur pleins de villes pour les performances)
C'est déjà ça faute de démonstration.

[Deedee81]

Ah tiens, question. En dehors des défis du style 250, trouve-t-on facilement sur le net des cas avec seulement quelques villes mais azvec des configurations assez piégeuses pour des algos trop simplistes ?
Parce que si j'ai 2000 villes sur une droite, là, c'est facile

[Biname]

Salut,
Le nombre d'itinéraires possibles est égale à la permutation du nombre de villes à parcourir ? Soit pour 7 villes : 7! = 5040 itinéraires. Le cas 7 villes se résout par la 'brute force' en quelques dizaines de microsecondes sur le PC 'qui va bien'. Pour 250 villes, il y a 3.23e492 itinéraires différents ... là, faudra aider la 'brute force' .

Poser le problème en utilisant des distances établies de manière aléatoire(Rand, Rnd, Random) est très simple en informatique, écrire le code de la solution ne me paraît pas bien difficile non plus ??? Le pb est le temps machine nécessaire pour résoudre le problème, lorsque le nombre de villes augmente.

Biname

[Médiat]

Bonjour,

Le nombre d'itinéraires possibles est égale à la permutation du nombre de villes à parcourir ? Soit pour 7 villes : 7! = 5040 itinéraires.

Non, c'est plutôt (n-1)!/2 pour les graphes non orientés, comme ici et (n-1)! pour les graphes orientés, pour 7 villes, ici on trouve 360.

[Deedee81]

écrire le code de la solution ne me paraît pas bien difficile non plus ???

Je suis d'accord, c'est même élémentaire. Mais ci-dessus je parlais bien entendu code pour l'algorithme de Adri0

[Médiat]

Je suis d'accord, c'est même élémentaire.

C'est bien pourquoi je proposais le défi des 250 villes, l'algorithme ne devant pas touné plus d'une minute dans ce cas

[GBo]

C'est bien pourquoi je proposais le défi des 250 villes, l'algorithme ne devant pas touné plus d'une minute dans ce cas

Et ce serait une très bonne preuve du concept. Et c'est à Adri0 de s'y coller, car c'est à lui de prouver que son algo est intéressant

[MissJenny]

Le nombre d'itinéraires possibles est égale à la permutation du nombre de villes à parcourir ?

c'est le cas si on a un chemin entre chaque paire de villes, mais dans certaines versions du problème ça n'est pas le cas et on peut être amené à passer plusieurs fois par la même ville.

[Deedee81]

Chose étonnante, pour un graphe quelconque il existe un algorithme optimal et polynomial de recherche du plus court chemin entre deux points.
(doit pas passer par toutes les villes !)
C'est utilisé dans les GPS par exemple
(c'est un ami mettant au point un algo de manipulation de bras robotique pour les tokamaks qui m'avait montré ça il y a, ooooohhhhh, fort longtemps )

Comme quoi des problèmes qui se ressemblent n'ont pas nécessairement les mêmes difficultés du tout

[Médiat]

..... Dijkstra ?

[Deedee81]

..... Dijkstra ?

Ah, j'ai regardé de près. Il est un peu plus général que la version que je connaissais (qui n'était applicable qu'à un graphe plongé dans un espace métrique) mais c'est bien ça.
Merci,

[Médiat]

En plus ça se programme en 10mn douche comprise, euh documentation comprise.

[Deedee81]

En plus ça se programme en 10mn douche comprise, euh documentation comprise.

faut quand même initialiser le graphe, si tu fais ça en lignes de code ça peut prendre un peu de temps

Mais l'algo en soi oui, c'est simple. A l'époque j'avais trouvé ça extraordinaire.

[Opabinia]

Bonjour,

Si tu veux trouver la solution optimale sur un ensemble de 7 villes, par exemple, tu peux commencer par en établir la liste classée par ordre alphabétique et en déduire le tableau des distances, matrice carrée symétrique à éléments diagonaux nuls.

La boucle fermée, dont la longueur ne dépend pas du point de départ, commence à la première ville d'indice nul; on considère d'abord les deux points reliés au précédent par un trajet direct, donc celui qui intervient en seconde position (d'indice Ia) et le dernier (d'indice Ib): le trajet sera ainsi représenté par la séquence

< 0 , Ia , J1 , J2 , J3 , J4 , Ib , 0 > .

Chaque boucle pouvant être parcourue dans un sens ou dans l'autre, on conviendra de ne retenir que celles vérifiant

Ia < Ib

afin d'éviter tout calcul inutile; l'énumération des premiers indices s'effectuera donc sur les domaines:

0 < Ia < Nv - 1 et Ia < Ib < Nv .

Pour les 3 suivants (J1, J2, J3) il faudra balayer l'intervalle [1 ; Nv - 1] en évitant les valeurs mutuellement identiques, ou égales à celles des précédents indices (Ia, Ib).
Le dernier s'obtient par simple différence, compte tenu de ce que la somme de tous les termes est constante:

Ia + Ib + J1 + J2 + J3 + J4 = 1 + 2 + ... + 6 = 21 .

L'énumération de tous les cas s'effectue rapidement dans le cas envisagé:

L'algorithme, bien que comportant déjà 5 boucles imbriquées, n'est pas très compliqué; mais on voit facilement qu'il ne peut conduire à la solution rigoureuse dans le cas le plus général, en raison d'un allongement considérable et de plus en plus rapide du temps de calcul; l'introduction d'une nouvelle ville s'accompagne de l'insertion d'une boucle supplémentaire, et l'exécution du programme cale en pratique au-delà d'une douzaine de villes - je ne me rappelle plus la limite exacte.

PS: La première ligne des résultats (zone noire) affiche les dernières valeurs énumérées de (Ia) et (Ib).

[Biname]

Salut,

Bonjour,
Non, c'est plutôt (n-1)!/2 pour les graphes non orientés, comme ici et (n-1)! pour les graphes orientés, pour 7 villes, ici on trouve 360.

Oui ! Heureusement, j'avais laissé un point d'interrogation
- tous les chemins sont des boucles qui peuvent être parcourues dans les deux sens, on divise par deux
- un chemin/boucle peut débuter en chacun des points de ce chemin, chacun de ces chemins présente la même distance à parcourir (n-1)

En pratique pour un programme :
Ai nodes/villes pour i = 1 à n, tous les chemins commencent par/à A1 et l'index du second node du chemin est toujours inférieur à l'index du dernier node, ... dans le cas d'une énumération croissante de gauche à droite ... comme ci-dessous (dans les autres cas aussi ????).

essai avec a b c d (n-1)/2 = 3 A1 = a, A2 = B, A3 = c, A4 = c
a b c d
a b d c
a c b d exclu 'a c d b' car index de b (dernier) < index de c (second)

essai avec a b c d e (n-1)/2 = 12
01: a b c d e
02: a b c e d
03: a b d e c
04: a b d c e
05: a b e c d
06: a b e d c
07: a c b d e
08: a c b e d
09: a c d b e exclu 'a c d e b' car ic > ib et = 06
10: a c e b d exclu 'a c e d b' car ic > ib et = 03
11: a d b c e exclu 'a c d e b' car ic > ib et = 06 exclu 'a d b e c' car id > ic et = 10
12: a d c b e
: a e x x x toujours exclus car ix tjrs < ie

Ouf ! avec les index c'est peu clair A1 A3 A2 A4 ???

Biname