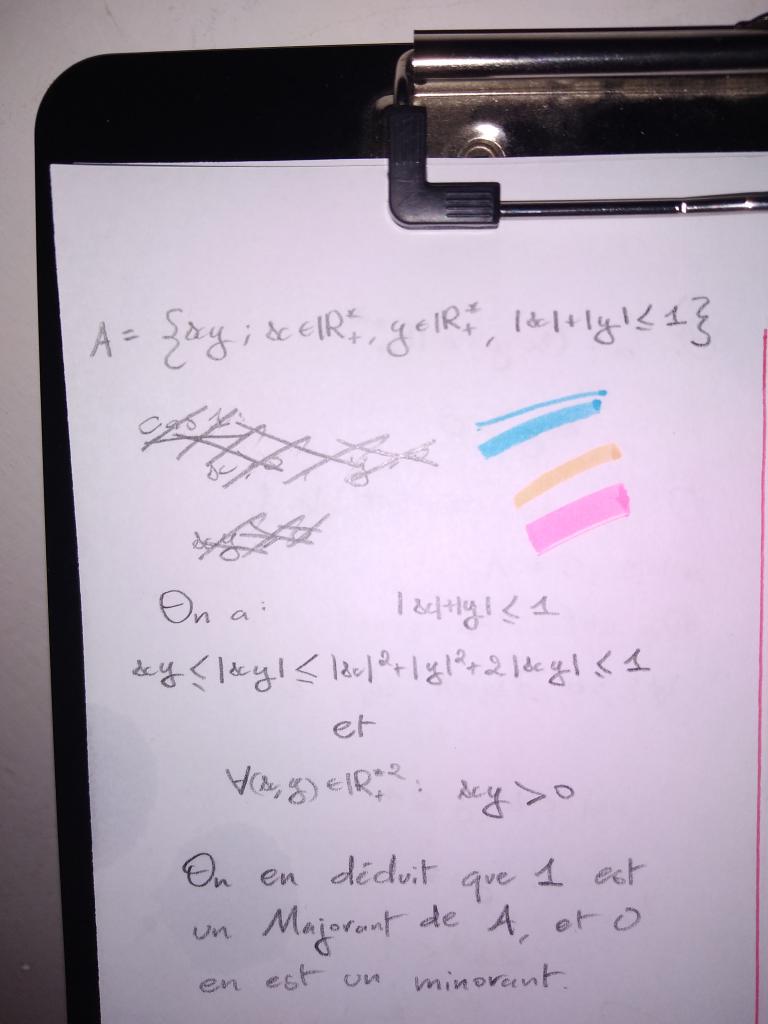Vous m'excuserez d'avance, je débute dans ce chapitre des Nombres Réels et je ne suis pas top au maths, c'est pour ça que je demande souvent de l'aide ici même si j'en fais peut-être un peu trop.
Bref, la seule chose que j'ai pu trouver par moi-même de cet ensemble c'est que xy>0 donc 0 est un minorant de A, voilà.
Et je sais aussi qu'il y a beaucoup à tirer de |x|+|y|<=1 mais je n'y arrive pas
Tu essaies avec x>=0 et y>=0 puis tu traites les 3 autres cas qui vont être simples vu les symétries.
Mais x et y sont tous les deux déjà strictement supérieurs à 0, ils appartiennt à R+/{0}
Bonsoir .
Regarde un peu ce qu'est la norme 1 de Hölder ...et là tu as affaire à la l'intérieur de boule unité pour la norme idoine ...tu verras peut-être plus clair .
OUI...un seul cas ici le quart de plan des x et y positifs...tu es dans un triangle du coup
La boule !
Hein ? Mais j'ai jamais vu ça auparavant
J'ai recherché sur Google, et j'ai trouvé que c'était qq chose avec les espaces vectoriels, ça ne concerne pas encore...
En fait, dans cet énoncé, les valeurs absolues sont inutiles. Et les propriétés des inégalités donnent immédiatement le résultat.
Cordialement.
En effet. J'ai raté le + qui est tout petit et quelque part aberrant si on met des valeurs absolues.
Suis-je, ne serait-ce qu'un peu, sur la bonne voie ?
oui, 1 est bien un majorant mais est-ce le plus petit ? 0 est la borne inf ... à montrer
x>0 et y>0 donc forcément leur produit xy>0, alors 0 est un minorant
Mais bon montrer que 1 est le plus petit des Majorants et 0 le plus grand je ne sais pas comment... La caractérisation ?
O K ! Bonjour 1.
D'abord il faudrait faire une représentation dans le plan ce ce qu'est A . On ne voit rien sur ta feuille , je ne sais si je dois me placer à un niveau de lycée ou de l'enseignement supérieur car j'ai parlé de la norme N1au-dessus donc oublions ceci .
En classe de première par ex comme x et y sont strictement positifs , A sera l’intérieur du triangle O I J où on a I(1 ; 0 ) et J ( 0 ; 1 ) et O (0 ; o ) bien sûr , il faut ajouter à ça le côté ]I ;J [ mais non les deux autres côtés. Ceci s'appelle la zone des contraintes car on veut que x + y<= 1 avec x et y strictement positifs .
(suite ) dans ta structure mentale il doit se passer alors ceci ; si M(x;y) se " promène" dans A ensemble borné du plan ....où va- t-il se trouver pour que x*y soit le plus grand possible ? là je te donne MON raisonnement et peut-être qu'il y en a d'autres ?
Remarque : (a+b)² = a²+2ab+b² ( tout nourrisson tant soit peu évolué, sait ça ! ) idem pour (a-b)² de là il est facile de voir que ab = [ (a+b)² - ( a-b)² ] / 4 démontre le si tu t'octroies le bénéfice du doute .
Et je vois que le produit de deux nombre est maximum si ....(a-b)² est le plus petit possible donc nul et donc si a = b.
Salut Derona,
Attention. Ce que tu dis est juste et utile. Mais certains de tes propos sont assez agressifs pour dire le moins. Ce n'est peut-être pas volontaire mais ça pourrait être mal pris et attention aux retours de bâtons verts
"Il ne suffit pas d'être persécuté pour être Galilée, encore faut-il avoir raison." (Gould)
donc x*y =xy est max si x=y donc si M(x;y) se trouve sur la première bissectrice ( la droite d'équation y=x si tu veux) et là il y aura une position limite pour ce M , c'est sur ( IJ ) donc si M = E(0.5 ; 0.5 ) qui te dira que xy <= 0.5 * 0.5 = 0.25 et c'est ça le plus petit des majorants donc la borne suo de A et comme il appartient à A ce sera le maximum .
A présent comme x et y > 0 c'est que xy> 0 et donc 0 est le plus grand des minorants . Pourquoi ? il faut te dire que pour tout x et y dans A , 0< xy s'il y avait un autre minorant plus grand que 0 en général on l'appelle epsilon ceci voudrait dire que 0< epsilon < xy ceci pour tout x et y > 0 ce qui est faux ..par ex je prends epsilon/2 =x et y = 1/2 avec epsilon petit , et là xy= epsilon / 4 < epsilon <xy d'où la contradiction car j'ai trouvé x et y de produit plus petit que epsilon .
Conclusion : 0 est la borne inférieure de A et comme 0 n'est pas dans A ce n'est pas le minimum .
Bon , écoutez- moi bien Mr le modérateur....pour ne pas passer en justice pour moi , ce qui est la mode en ce moment en France, on va s'arrêter là ...vous allez supprimer mon compte, si la plaisanterie est prohibée et la langue française si souvent injustement matraquée dans ce forum....je me retire comme je vous l'avais déjà dit il y a des mois de ça . Veuillez verrouiller mon nom...J'en ai assez de perdre mon temps ici , j'ai d'autres préoccupations .GOOD BYE
Je ne suis pas modérateur de ce forum, je disais juste ça pour aider (d'autant que l'humour sans le ton, par écrit, ça ne passe pas toujours). Et je ne sais pas supprimer un compte.
Mais bon, j'ai mis un avertissement pour la modération. Désolé que tu n'aies pas toi même l'humour que tu dispenses si généreusement. Enfin, bon, bonne continuation
"Il ne suffit pas d'être persécuté pour être Galilée, encore faut-il avoir raison." (Gould)
Bonjour.
Pour en revenir au sujet, une preuve peut être construite ainsi :
On a x+y=k avec k compris entre 0 et 1. Pour k fixé, y=k-x et xy=x(k-x) qui est maximum pour x=k/2. Ce maximum est k^2/4 et augmente avec k. Ce qui fait que le maximum global est atteint pour k=1. Etc.
Cordialement
