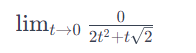Limite à plusieurs variable méthode de substitution

[CobeLegrand]

Bonjour je connais les différentes méthodes pour déterminer la limite d'une fonction à plusieurs variables mais j'ai des problémes avec l'une d'entre elle.
Je comprends pas trop bien la méthode de substitution


J'ai sais que c'est une méthode qui est utilisée seulement pour montrer que la fonction n'a pas de limite définie mais je ne sais pas avec quoi remplacer t

par exemple ici : Capture d'écran 2023-12-20 164015.png Capture d'écran 2023-12-20 164155.png

Pourquoi on dit que c(t) = (0,0) ou c(t) = (t,0), je veux dire comment déterminer les valeurs de x et y que doit prendre t ?

Merci pour votre aide.
-----

[gg0]

Bonjour.

II n'y a pas de règle. Tout dépend de l'expression concernée.
En fait, tu as compris la méthode, mais tu crois que quelque chose reste caché. Rien n'est caché.

Cordialement.

[CobeLegrand]

En fonction de l'expression de la fonction, c'est à dire ?

Par exemple pour la fonction :
Je ne peux pas prendre c(t) = (t,t) pourquoi ?

[gg0]

Tu cherches toujours la limite en (0,0) ?
"Je ne peux pas prendre c(t) = (t,t) pourquoi ? " Ben si, tu peux faire ça. Si ça te fait envie ...

Tu fais ce que tu veux, et tu vois si ça te permet de conclure. Encore une fois, "II n'y a pas de règle". Rien ne t'interdit d'imiter ce qui a été fait dans d'autres exercices, encore faut-il que ça serve à quelque chose.

Alors, comment fais-tu dans ce cas ?

[A voir en vidéo sur Futura]

[GBZM]

Bonjour,
Dans ce genre de problème de continuité à l'origine, on a plusieurs cordes à son arc.
On peut passer en coordonnées polaires. Ça sera commode pour ton deuxième exemple.
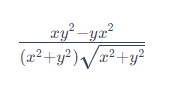
On peut tendre vers l'origine en suivant des courbes paramétrées : si on trouve des limites différentes en approchant le long de deux courbes différentes, alors la fonction ne peut pas se prolonger par continuité à l'origine. Le chois de ces courbes demande un peu de flair. Par exemple pour le deuxième cas : on voit que sur les droites , et la fonction est nulle et donc la limite quand on approche l'origine le long de ces droites est toujours nulle. On peut donc essayer une autre droite, par exemple , et voir ce qui se passe quand on approche l'origine le long de cette droite.

[CobeLegrand]

Ba si on prend c(t) = (t,t), on remplace x et y par (t,t) ça fait :
Mais cette expression tend vers 0 ? Alors que la limite ne devrait pas être de 0.

[GBZM]

Relis ce que j'ai écrit et réfléchis-y un peu plus sérieusement.
Peux_tu calculer la limite de quand on approche l'origine suivant la droite ?

[CobeLegrand]

Oui, je trouve 2/(5.racine(5)) . Je me suis peut-être trompé sur le calcul mais je crois avoir compris, on cherche donc des droites pour lesquelles la fonction n'est pas nulle.

[GBZM]

Ici oui. Mais tout dépend de la fonction étudiée. Des fois, on a intérêt à étudier la limite suivant des courbes arrivant à l'origine qui ne sont pas des droites.