poussée d'archimède

[calculair]

Mauvaise réponse !

Fais le bilan énergétique entre l'état initial et l'état final, indépendament des forces dissipatives, qui ne sont pas mentionnées dans la question.

On considère les emplacements M et L où est amarré le navire à Marseille, puis à Lyon.

Etat initial : M est occupé par la partie immergée du navire. L est occupé par un volume d'eau équivalent.
Etat final : M est occupé par un volume d'eau équivalent à la partie immergée du navire. L est occupé par la partie immergée du navire.

Bilan : la masse du navire s'est élevée de 160 mètres, tandis qu'un volume d'eau s'est abaissé de 160 mètres.
Or le navire flotte, donc le poids de l'eau déplacée est égal au poids du navire. Donc du point de vue de l'énergie potentielle de pesanteur, le bilan est nul.

Les moteurs n'ont donc fourni aucune énergie pour élever le navire !

L'explication la plus courante est que la poussée d'Archimède compense exactement le poids du navire.

Or, et c'est là que cela devient rock'n roll, le fleuve peut être considéré dans notre analyse comme identique à lui-même par translation. La pression à la surface de l'eau et au fond est la même à Lyon et à Marseille, à la différence de pression atmosphérique près.
Par conséquent, l'intégrale des forces de pressions, qui définit la poussée d'Archimède, est perpendiculaire à la surface du fleuve. Donc elle ne compense pas le poids, qui doit être vaincu par les moteurs !

Je mets un 20/20 à l'oral à celui ou celle qui me résoud ce paradoxe !

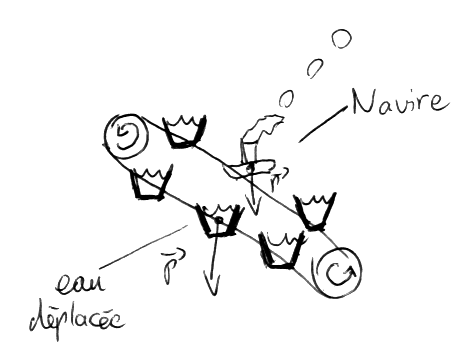
J'ai une façon de voir qu'effectivement, les moteurs du bateau n'ont pas travaillé pour monter le bateau.

Imaginons une enorme balance dont la longueur du fleau est la distance Marseille Lyon.

Cote marseille sur le plateau il y a un bassin plein d'eau avec le bateau flotant dessus.

Coté lyon le plateau contient le même bassin avec la même hateur d'eau ( Le volume du bateau a ete remplacé par l'eau )

A l'equilibre le fleau est horizontal ( les 2 plateaux à 0m d'altitude )

Il suffit d'une masse epsilon pour faire monter l'un des plateaux à l'altitude X ( en supposant g constant) , d'ailleurs même si g evolue cela ne change rien, puisque il y a la même masse sur les 2 plateaux.
-----

[Pio2001]

Tout-à-fait, Calculair, c'est une bonne analogie.

Alors pourquoi la méthode de l'intégrale des forces de pression donne-t-elle un résultat faux ?

[Pio2001]

Voici le problème :



La force du moteur est censée compenser la force d'entraînement du courant.
Or la résultante des deux forces restantes est dirigée vers la droite. Le moteur doit donc lutter aussi contre elle. Or ce n'est que la projection sur la surface du fleuve de la force du poids !

Alors ? Lutter contre le poids ou ne pas lutter contre le poids ?

[sitalgo]

Donc du point de vue de l'énergie potentielle de pesanteur, le bilan est nul.

Les moteurs n'ont donc fourni aucune énergie pour élever le navire !

C'est pour moi un raccourci saisissant, ce n'est pas parce que l'état final est égal à l'état initial qu'on n'a pas dépensé d'énergie.
Ce serait valable si l'énergie du volume d'eau était récupérable, comme dans le cas de 2 masses reliées par une corde avec une poulie.

Complément du schéma, le bateau doit être incliné, quasiment parallèle à la surface de l'eau. Les positions relatives du centre de
poussée et du centre de gravité vont faire piquer ou relever la proue. Vu la pente d'un fleuve, ça fait pas lourd.
Si on inventait l'eau immobile en pente, le bateau (moteur arrêté) descendrait la pente comme un mobile sur un pan incliné.

[invite6754323456711]

bonjour,

Si on applique le principe des écluses le moteur n'est pas non plus utilisé pour passer du niveau 0 au niveau 160 mètre.


Patrick

[sitalgo]

Si on applique le principe des écluses le moteur n'est pas non plus utilisé pour passer du niveau 0 au niveau 160 mètre.

Oui, mais là il n'y a pas de paradoxe apparent, la poussée d'Archimède fournit bien un travail.

Mais on peut là aussi trouver un paradoxe à première vue : qu'il y ait ou non un bateau dans l'écluse, la remplir et la vider fait passer le même volume d'eau. Le système consomme donc la même énergie (potentielle) pour faire monter une barque ou une péniche de 200 tonnes.
A deuxième vue il suffit de remplacer le bateau par son volume d'eau et tout est normal. En somme le bateau est un moyen de séparer physiquement l'eau heu... normale de l'eau heu... du volume déplacé.

[calculair]

Voici le problème :



La force du moteur est censée compenser la force d'entraînement du courant.
Or la résultante des deux forces restantes est dirigée vers la droite. Le moteur doit donc lutter aussi contre elle. Or ce n'est que la projection sur la surface du fleuve de la force du poids !

Alors ? Lutter contre le poids ou ne pas lutter contre le poids ?

ton schema est trompeur est amusant

le poids est dirigé vers le centre de la terre
la surface du liquide fait un angle avec la tangeante horizontale locale

le poids et la resultante des forces de pression sont perpendiculaires à la tangeante horizontale locale

les projections de cette resultante et le poids sur la surface montante du liquide sont egales et opposées

quand le bateau se deplace la poussée d'archimède travaille en sens opposé du poids !!!!

es tu d'accord Pio 2001 ?

[calculair]

C'est pour moi un raccourci saisissant, ce n'est pas parce que l'état final est égal à l'état initial qu'on n'a pas dépensé d'énergie.
Ce serait valable si l'énergie du volume d'eau était récupérable, comme dans le cas de 2 masses reliées par une corde avec une poulie.

Complément du schéma, le bateau doit être incliné, quasiment parallèle à la surface de l'eau. Les positions relatives du centre de
poussée et du centre de gravité vont faire piquer ou relever la proue. Vu la pente d'un fleuve, ça fait pas lourd.
Si on inventait l'eau immobile en pente, le bateau (moteur arrêté) descendrait la pente comme un mobile sur un pan incliné.

je ne suis pas si sur ......j'en suis à me dmander si le bateau ne rmonte pas la pente

La resultante des forces de pression est un chouilla superieure à l'arrière du bateau par rapport à l'avant. en effet l'arriere etant plus bas que l'avant en raison de la pente du fleuve se trouve plus prés du centre de la terre, et donc g (arriere) > g (avant). La pression excercée par l'eau etant proportionnelle à la valeur du g local, il existe une poussée, mais faible qui pousse le bateau vers les altitudes croissantes. !!!!!!!!!!

[sitalgo]

Le schéma est bon, la poussée d'Archimède est bien perpendiculaire à la surface de l'eau.

[sitalgo]

La resultante des forces de pression est un chouilla superieure à l'arrière du bateau par rapport à l'avant. en effet l'arriere etant plus bas que l'avant en raison de la pente du fleuve se trouve plus prés du centre de la terre, et donc g (arriere) > g (avant). La pression excercée par l'eau etant proportionnelle à la valeur du g local, il existe une poussée, mais faible qui pousse le bateau vers les altitudes croissantes. !!!!!!!!!!

Oui, mais vu l'ordre de grandeur des forces dues à un différentiel de gravité et les forces en jeu, je ne sais pas si ça fera changer la 12ème décimale. En tenant compte d'une poussée perp à la surface de l'eau, ce qui est facilement vérifiable même graphiquement.

[calculair]

Le schéma est bon, la poussée d'Archimède est bien perpendiculaire à la surface de l'eau.

oui mais le poids doit être aligné avec Archimède, c'est là l'erreur

[calculair]

Oui, mais vu l'ordre de grandeur des forces dues à un différentiel de gravité et les forces en jeu, je ne sais pas si ça fera changer la 12ème décimale. En tenant compte d'une poussée perp à la surface de l'eau, ce qui est facilement vérifiable même graphiquement.

la question n'est pas de recuperer de l'energie, mais de faire un bilan théorique des forces. Si c'est la 13° decimale qui est changée, c'est tout aussi significatif que si s'etait le chiffre le plus significatif.

Le point fondamental c'est qu'il existe une micro force qui a tendance à faire monter le bateau, ( dommage que le courant perturbe tout )

[obi76]

oui mais le poids doit être aligné avec Archimède, c'est là l'erreur

Pourquoi il le devrai ? là il ne l'est pas et pourtant Archimède est bien comme ça et le poids est vers le bas (jusqu'à preuve du contraire)

le fluide n'est pas à l'équilibre là, ça influe je pense sur la direction de la poussée...

[sitalgo]

oui mais le poids doit être aligné avec Archimède, c'est là l'erreur

Je t'ai répondu précédemment : En tenant compte d'une poussée perp à la surface de l'eau, ce qui est facilement vérifiable même graphiquement.
Si tu le contestes, fais au moins l'effort de le vérifier.

j'en suis à me dmander si le bateau ne rmonte pas la pente

Le problème de la décimale est pour répondre à ce que tu as écrit. Ce que j'ai répondu est valable même pour une eau immobile en pente, alors si on ajoute le courant...
De toute façon, un gradient de gravité ne change rien puisque l'arrière du bateau est lui aussi plus près du centre de la terre donc pèse plus lourd.

[invite6754323456711]

Oui, mais là il n'y a pas de paradoxe apparent, la poussée d'Archimède fournit bien un travail.

Si tu décompose le problème en sigma de plan horizontal (fonction en escalier) et que tu intègre (marche de l'escalier de plus en plus petit, une infinité d'écluse) du devrait arriver sans paradoxe au schéma de pio2001


Patrick

[Pio2001]

le poids et la resultante des forces de pression sont perpendiculaires à la tangeante horizontale locale
(...)
es tu d'accord Pio 2001 ?

Non, car la répartition des pressions, schématisée par les lignes isobares, est identique à celle dans un récipient au repos, à une rotation près correspondant à l'angle que forme la surface du fleuve avec l'horizontale.

Par conséquent, leur résultante est identique à celle dans un récipient au repos à la même rotation près. Donc elle est bien perpendiculaire à la surface du fleuve, au gradient de pression atmosphérique près (qui domine le gradient de champ gravitationnel appliqué à l'eau, je pense), et non verticale.

C'est pour moi un raccourci saisissant, ce n'est pas parce que l'état final est égal à l'état initial qu'on n'a pas dépensé d'énergie.
Ce serait valable si l'énergie du volume d'eau était récupérable, comme dans le cas de 2 masses reliées par une corde avec une poulie.

L'énergie du volume d'eau est bien récupérée par le bateau. Le déplacement de l'eau et celui du bateau sont en effet contraints de se faire en sens inverse l'un de l'autre. Un déplacement dx du bateau provoque un déplacment -dx d'une quantité d'eau égale au volume déplacé. C'est valable pour chaque déplacement infinitésimal, et pas seulement entre l'état initial et l'état final.

On peut donc bien considérer que tout se passe comme si le bateau et l'eau déplacée étaient reliés par une corde avec une poulie.


Vous avez donc tous les deux raison. Alors où est l'erreur ?

Eh bien il manque une force dans mon schéma. Une force égale et opposée à la résultante du poids et des forces de pression, qui feraient sans elle glisser le bateau vers le bas en l'absence de courant.



Cette force n'existe pas en hydrostatique, c'est pourquoi je l'ai appelée "force hydrodynamique". Elle résulte de la liberté pour l'eau en amont du bateau de s'écouler dans le volume qu'il occupe, et de le repousser ainsi vers le haut.
D'un point de vue énergétique, nous avons déjà représenté la résultante des forces de pression. Nous pouvons donc nous intéresser aux variations d'énergie potentielle de pesanteur lorsque l'eau se déplace parallèlement aux isobares. On voit que lorsque le bateau monte la pente, l'eau perd de l'énergie potentielle de pesanteur. Qui dit variation d'énergie potentielle dit force associée.

Alors la poussée d'Archimède est-elle perpendiculaire à la surface ou verticale ?
Mon opinion, n'ayant pas étudié l'hydrodynamique, est la suivante : le principe d'Archimède est un principe purement hydrostatique. Il est défini et valable notamment lorsque la surface du liquide est horizontale. Je n'en connais aucune définition correspondant au cas d'un liquide de surface inclinée.
Dans notre cas, où la surface est inclinée, nous devons généraliser le principe d'Archimède. Nous pouvons alors convenir à notre gré de le définir la poussée d'Archimède comme la résultante des forces de pression. Elle sera alors perpendiculaire à la surface de l'eau, et n'incluera pas la force hydrodynamique mentionnée. Ou bien comme la réaction sur le navire du poids de l'eau déplacée. Elle sera alors verticale et comprendra notre force hydrodynamique.

Conclusion : le moteur ne travaille pas contre le poids.

[Pio2001]

Conclusion bis : raisonner en termes de forces de pression ne conduit pas toujours au bon résultat !

Je trouve que raisonner en variations d'énergie est plus général.

[invite6754323456711]

J'ai une façon de voir qu'effectivement, les moteurs du bateau n'ont pas travaillé pour monter le bateau.

Imaginons une énorme balance

La roue de Falkirk (Ecosse) n'est pas une balance mais un ascenseur à bateaux rotatif : http://www.madamemartin.com/lien.php/365


Patrick

[sitalgo]

Qui dit variation d'énergie potentielle dit force associée.

Soit une masse, on la jette du haut d'une falaise, mgh etc.

Je relie à cette masse une force B vers le haut égale à son poids, par ex un ballon.
F = P + B = 0
Je donne l'impulsion initiale et la masse descend. Perte d'énergie potentielle, pas de force.

Elle résulte de la liberté pour l'eau en amont du bateau de s'écouler dans le volume qu'il occupe, et de le repousser ainsi vers le haut.

Soit une masse, sphérique histoire de, en bas et dans l'axe d'un tube rempli de liquide plus dense que la masse. On lache la masse qui remonte.
A priori, ta force dynamique est censée se manifester. D'autant que par raison de symétrie on peut considérer qu'il s'agit de 2 demi-cylindres séparés par un plan vertical donc chaque moitié de sphère est dans son demi-cylindre comme la coque d'un bateau dans l'eau.
Cette force n'a jamais été mise en évidence.

------------------------------

Je raisonne avec de l'eau en pente et immobile (dont je vais déposer le brevet) mais on pourrait faire une expérience significative avec un fluide très visqueux.
J'ai de l'eau en pente et je pose une balle, immobile, de densité 0,5 (à moitié immergée, c'est plus facile pour le dessin). D'après le bilan des forces (puisqu'il n'y a pas de force dynamique) je vois qu'elle va descendre.

Il faut donc une force rien que pour maintenir la balle immobile. Donc une force supplémentaire pour lui donner une vitesse puis reforce initiale pour maintenir sa vitesse.

Ce qui veut dire qu'un bateau sur de l'eau en pente est comme un hélicoptère en vol stationnaire, il doit consommer de l'énergie pour rester au même endroit. A part que pour le bateau cette part d'énergie est très faible.

[pmdec]

Salut !

Juste une petite remarque : quand le bateau se déplace par rapport à l'eau, est-ce qu'il ne flotterait pas moins (sans tenir compte des effets de portance éventuels), à cause de la diminution de la pression statique ?

[sitalgo]

Après une bonne nuit de réflexion en dormant.

A l'arrêt, le bateau a besoin d'une force A pour ne pas tomber et rester immobile et d'une force B pour lutter contre les frottements visqueux dus au courant.
Pour prendre de la vitesse il a besoin d'une force C supplémentaire pour accélérer sa masse.
Une fois la vitesse de croisière atteinte il n'a plus besoin de cette force C, il n'a besoin que de A et B (avec B augmenté à cause de la vitesse).

On peut donc dire que la force A ne sert pas à gagner de l'énergie potentielle mais à éviter de perdre celle acquise. Elle permet d'annuler l'effet de la gravité, la masse conservant sa vitesse par inertie.

[calculair]

Pour moi la poussée d'Archimède n'est pas perpendiculaire au plan d'eau mais alignée avec le poids. Il n'existe pas de force qui tend à faire glisser le bateau vers le bas. ( hors la force d'entrainement du courant )

Remarque: lorsque un objet flotte sur l'eau quand une vague un peu longue arrive, l'objet reste immobile et ne tend pas à descendre le long de la vague

Par ailleurs le coté le plus en aval du bateau reçoit une force de pression dans l'axe u bateau ( vers l'amont ) un mini pouillème superieure que la poussée exercée par la pression sur l'avant du bateau ( situé en amont ) cette dernière est dirigée vers l'aval

le resultat c'est qu'il existe une toute mini micro force qui tend à faire remonter le courant au bateau. Cette force est liée à la variation de " g" entre l'amont et l'aval du bateau

[obi76]

Pour moi la poussée d'Archimède n'est pas perpendiculaire au plan d'eau mais alignée avec le poids. Il n'existe pas de force qui tend à faire glisser le bateau vers le bas. ( hors la force d'entrainement du courant )

Remarque: lorsque un objet flotte sur l'eau quand une vague un peu longue arrive, l'objet reste immobile et ne tend pas à descendre le long de la vague

Ca dépend de la largeur de la vague par rapport à la largeur de l'objet. Si la vague est grande devant la taille de l'objet, les lignes isobares dans le fluide restent quasiment parallèles à l'objet, donc la poussée d'archimède aussi.
Inversement, si la vague est du même ordre de grandeur, alors la déformation des lignes isobares sera significatives, l'objet décrit une ellipse.
Si la vague est extrêmement petite, les variations des lignes isobares restent négligeables face à la poussée d'archimède totale.

[calculair]

Si on decoupe le bateau en tranches fines, le poids de chaque tranche est equilibrée par la poussée d'archimède qui est egale et opposée au poids

[Pio2001]

Soit une masse, on la jette du haut d'une falaise, mgh etc.

Je relie à cette masse une force B vers le haut égale à son poids, par ex un ballon.
F = P + B = 0
Je donne l'impulsion initiale et la masse descend. Perte d'énergie potentielle, pas de force.

Si, la masse est toujours soumise à son poids. Un spationaute en apesanteur est lui aussi soumis à son poids, sinon il ne tournerait pas autour de la Terre. Ce n'est pas parce que le bilan des forces est nul que les forces sont nulles.

Soit une masse, sphérique histoire de, en bas et dans l'axe d'un tube rempli de liquide plus dense que la masse. On lache la masse qui remonte.
A priori, ta force dynamique est censée se manifester.

Non, car la surface du liquide, en haut du tube, n'est pas inclinée. D'ailleurs, j'ai défini cette force comme résultant de mouvements parallèles aux isobares. Dans le tube, les isobares sont horizontales, et engendrent la simple poussée d'Archimède hydrostatique.

D'autant que par raison de symétrie on peut considérer qu'il s'agit de 2 demi-cylindres séparés par un plan vertical donc chaque moitié de sphère est dans son demi-cylindre comme la coque d'un bateau dans l'eau.

Ce n'est pas le même cas de figure, car les deux demi-cylindres exercent une pression l'un sur l'autre. La surface du demi-cylindre n'est donc pas à la pression atmosphérique.

Je raisonne avec de l'eau en pente et immobile (dont je vais déposer le brevet) mais on pourrait faire une expérience significative avec un fluide très visqueux.

Prenons de l'eau immobile en pente, car les forces de frottement visqueux vont masquer l'effet de la force que l'on veut mettre en évidence.

J'ai de l'eau en pente et je pose une balle, immobile, de densité 0,5 (à moitié immergée, c'est plus facile pour le dessin). D'après le bilan des forces (puisqu'il n'y a pas de force dynamique) je vois qu'elle va descendre.

Il faut donc une force rien que pour maintenir la balle immobile. Donc une force supplémentaire pour lui donner une vitesse puis reforce initiale pour maintenir sa vitesse.

Ce qui veut dire qu'un bateau sur de l'eau en pente est comme un hélicoptère en vol stationnaire, il doit consommer de l'énergie pour rester au même endroit. A part que pour le bateau cette part d'énergie est très faible.

Sans la force hydrodynamique, on aurait violation de la conservation de l'énergie. L'état initial et l'état final ont la même énergie. Alors où passe l'énergie supplémentaire fournie par le moteur ?

Un autre exemple de force hydrodynamique intervient dans le mouvement perpétuel sous-marin à soufflets. En ne prenant en compte que le poids et la poussée d'Archimède, et en négligeant la force hydrodynamique, ce système génère une énergie infinie : http://www.lhup.edu/~dsimanek/museum/annex.htm#bellows

Juste une petite remarque : quand le bateau se déplace par rapport à l'eau, est-ce qu'il ne flotterait pas moins (sans tenir compte des effets de portance éventuels), à cause de la diminution de la pression statique ?

Quelle diminution ?

Pour moi la poussée d'Archimède n'est pas perpendiculaire au plan d'eau mais alignée avec le poids.

C'est une convention possible. La poussée d'Archimède n'est alors plus égale à la résultante des forces de pression.

Il n'existe pas de force qui tend à faire glisser le bateau vers le bas. ( hors la force d'entrainement du courant )

Si, son poids. Mais il est contrebalancé par la poussée d'Archimède, telle que définie précédemment. Bilan nul ne signifie pas force nulle.

Par ailleurs le coté le plus en aval du bateau reçoit une force de pression dans l'axe u bateau ( vers l'amont ) un mini pouillème superieure que la poussée exercée par la pression sur l'avant du bateau ( situé en amont ) cette dernière est dirigée vers l'aval

le resultat c'est qu'il existe une toute mini micro force qui tend à faire remonter le courant au bateau. Cette force est liée à la variation de " g" entre l'amont et l'aval du bateau

Je ne pense pas, car cela violerait la conservation de l'énergie. La masse qui monte étant égale à la masse qui descend.

Si on decoupe le bateau en tranches fines, le poids de chaque tranche est equilibrée par la poussée d'archimède qui est egale et opposée au poids

Des tranches verticales ? Attention, elles exercent une pression les unes sur les autres, car elles sont décalées d'une hauteur dh les unes par rapport aux autres.
La pression à la hauteur z d'une tranche est donc inférieure à la pression à la même hauteur de la tranche amont, car elle est en vis-à-vis de l'élément de hauteur z-dh de celle-ci, et supérieure à la pression à la même hauteur de la tranche aval, car elle est en vis-à-vis de l'élément de hauteur z+dh de celle-ci ! Cela rend l'analyse très complexe, d'autant qu'il faut prendre en compte la force hydrodynamique qui résulte d'un mouvement oblique à travers les tranches.

[Pio2001]

Voici un modèle d'eau immobile en pente :



Par commodité, chaque bac contient une quantité d'eau de poids égal à celui du navire.
Les poulies et les cordes représentent la contrainte géométrique qui impose à l'épaisseur du fleuve de rester constante, de sorte que lorsqu'une certaine quantité d'eau monte, une quantité égale descend.

Le courant peut être représenté par un glissement de l'ensemble du montage, poulies comprises, vers l'aval, et par le fait que celui-ci serait infini.

On voit ici comment l'eau déplacée par le navire, qui descend lorsque celui-ci monte (la densité de bacs par unité de longueur de corde restant par ailleurs constante) exerce sur le navire une force dirigée vers l'amont.
Cette force est la seule ressentie par le navire, car les poids de tous les autres bacs s'annulent deux à deux.

Elle annule l'effet du poids du navire. Dans la représentation du fleuve continu, elle complète l'intégrale des forces de pression, qui est une description incomplète de la poussée d'Archimède si on considère celle-ci verticale.

[pmdec]

Bonsoir,

Juste une petite remarque : quand le bateau se déplace par rapport à l'eau, est-ce qu'il ne flotterait pas moins (sans tenir compte des effets de portance éventuels), à cause de la diminution de la pression statique ?

Quelle diminution ? .../...

Ben ... Bernouilli ! La vitesse de l'eau relativement à la coque doit nécessairement faire que la composante de la pression perpendiculaire à la coque diminue. Donc en intégrant sur la surface immergée on doit obtenir une force plus petite.

Autre remarque : je ne crois pas que la remontée du fleuve soit assimilable à une suite infinie d'écluses. Dans le cas d'une écluse unique, le bateau vogue en permanence sur de l'eau horizontale, puis pénêtre dans l'écluse. Là, c'est bien le remplissage de l'écluse qui fait monter le bateau (on récupère une partie du travail de l'eau qui descend***). Le couple (poussée d'Archimède + poids) est en permanence un couple de forces verticales : leur déplacement horizontal ne nécéssite aucun travail.

Par contre, si la poussée d'Archimède (pour peu qu'on puisse encore s'y référer) est bien perpendiculaire à la surface de l'eau, alors elle est décomposable en une force verticale et une force horizontale (dirigée vers l'arrière). Le déplacement "contre" cette force horizontale nécessite un travail ...


***petite remarque pour sitalgo (je crois) : la quantité minimale d'eau nécessaire pour faire monter le bateau ne dépend que de la surface du bateau (volume mini pour surface de l'écluse = surface du bateau) ce qui pourrait paraître paradoxal ...

[Pio2001]

Bonsoir,Ben ... Bernouilli ! La vitesse de l'eau relativement à la coque doit nécessairement faire que la composante de la pression perpendiculaire à la coque diminue. Donc en intégrant sur la surface immergée on doit obtenir une force plus petite.

En effet.

Autre remarque : je ne crois pas que la remontée du fleuve soit assimilable à une suite infinie d'écluses. Dans le cas d'une écluse unique, le bateau vogue en permanence sur de l'eau horizontale

C'est vrai, il y a une différence.
Dans mon dernier schéma, j'ai préféré dessiner le bateau tout seul que dans un bac pour éviter la confusion.

[chatelot16]

ce probleme des rivieres en pentes j'y ai pensé en lisant un roman qui se passait sur des bateau qui descendait le rhone avec le courant , a l'epoque ou c'est les chevaux qui tiraient pour remonter : pendant toute la descente le bateau etait maneuvré uniquement par le gouvernail : c'est bien la preuve qu'il avancait plus vite que le courant

la riviere a une legere pente , elle avance a la vitesse qu'il faut pour que le frotement de l'eau sur le fond equilibre les chose : si le bateau qui est sur cette pente avait le meme frottement que le fond de l'eau il avancerait a la meme vitesse par raport a l'eau et donc 2 fois plus vite par raport au sol

peut etre que si le fond est iregulier et le bateau bien profilé il avancera beaucoup plus vite que le courant : en tout cas c'est sur ca avance plus vite que le courant

quand au moteur du bateau qui remonte le courant : il a bien du travail : resistance aerodynamique de la coque , effet du poid et de la pente , et il doit pousser en prenant appui sur de l'eau qui recule

[Pio2001]

Oui mais c'est un roman... en vrai est-ce que ça marche ?

Et puis à quoi sert l'énergie que le moteur dépense en plus de celle destinée à vaincre le courant, puisqu'elle ne devient ni énergie cinétique (vitesse constante), ni énergie potentielle (bilan nul), ni énergie dissipée (comptée contre le courant) ?