Diffusion bidimensionnel , Fick

[Kley]

Salut,
je vous propose de me donner un tit coup de pouce sur ce problème avec lequel je me débat depuis un moment maintenant

Enoncé:
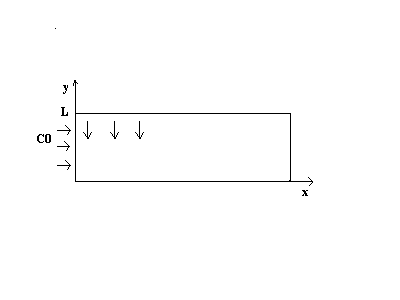
Soit le transfert de matière bidimensionnel et stationnaire d’un soluté A à travers un catalyseur B de largeur L et de longueur infinie. Le soluté pénètre par la surface de gauche avec une concentration C₀.
La surface de base est recouverte d’un film imperméable tandis que sur les surfaces restantes la concentration du soluté est nulle.
Trouver, en utilisant la méthode de séparation des variables, le profil de concentration
C(x,y).

Bon alors en va laisser la résolution mathématique de coté en premier lieu (étape par étape), je vous demande tout juste de m’aider à traduire (confirmer?)ce que j’ai comme conditions aux limites :

Le soluté pénètre par la surface de gauche avec une concentration C₀ :

I- A x =0 : C(0,y) = C₀

Sur les surfaces restantes la concentration du soluté est nulle. :

II- A :

III- A y=L : C(x,L) = 0

La surface de base est recouverte d’un film imperméable :

A y= 0, La je vois pas ?




Vous êtes Ok avec ces CL ??

merci,ciao
-----

[LPFR]

Bonjour
La condition limite à la surface imperméable est que la concentration ne change pas (pas de gradient de concentration).

Pour le reste je suis d'accord.
Au revoir.

[Kley]

Bonjour
La condition limite à la surface imperméable est que la concentration ne change pas (pas de gradient de concentration).

Salut LPFR

Tu peux m’expliquer ce qui te fait dire que la concentration est constante en y=0 ?.

Je ne comprend pas ; la matière diffuse de y>0 vers y=0, donc je ne vois pas comment la concentration pourrait resté inchangé en y=0 vu cet apport ?

J’ajouterais juste que en y=0 il y a un gradient de concentration selon les abscisses.

Un minimum?

A+

[LPFR]

Bonjour.
Attention, la concentration n'est pas constante pour y=0, elle ne varie pas en vertical, mais elle varie en horizontal.
Avez-vous remarqué qu'il s'agit de dérivées partielles?
Comme la paroi est imperméable, il ne peut pas avoir de courant de soluté qui la traverse. Donc le courant perpendiculaire à la surface est nul. Et si le courant est nul, le gradient dans la direction perpendiculaire à la surface doit être nul (voir équation de diffusion).
Dans votre problème, le soluté rentre à gauche et diffuse, de façon globale, vers la droite et vers le haut. Si la concentration est imposée égale à zéro sur la surface d'en haut, cela veut dire qu'il y a un processus externe qui extrait toutes les particules de soluté qui s'aventurent près de cette surface (par exemple on rince en permanence à l'eau claire la surface supérieure).
Votre distribution finale aura un gradient de concentration vers la gauche et vers le bas. Et le soluté disparaît vers le haut.
Au revoir

[A voir en vidéo sur Futura]

[LPFR]

Re.
Je viens de voir que vous allez être sérieusement emmquiquiné pour le point (0,L) qui doit satisfaire à deux conditions contradictoires. La concentration doit être Co et 0 simultanément!

Les flèches verticales de votre dessin sont l'inversées. Elles doivent pointer vers le haut.
A+

[Kley]

Les flèches verticales de votre dessin sont l'inversées. Elles doivent pointer vers le haut.
A+

Je reconnais que ça serait plus raisonnable,

Mais,je peux avoir quelques arguments appuyant le fait que la diffusion se fait vers le haut et non pas le contraire des y>0 vers les Y=0 ? (Je pense que cela doit être du au processus externe qui extrait toutes les particules de soluté en y=L créant ainsi le grad de concentrions décroissent NON ?) D’autres paramètres ?

[LPFR]

Mais,je peux avoir quelques arguments appuyant le fait que la diffusion se fait vers le haut et non pas le contraire des y>0 vers les Y=0 ?

Re.
La diffusion se fait toujours des endroits plus concentrés à moins concentrés. Or zéro c'est la concentration la plus faible du monde. Donc la diffusion se fait vers la surface y=L (et vers la droite aussi, puisque la concentration al plus haute est pour x=0).
A+

[Kley]

Les flèches verticales de votre dessin sont l'inversées. Elles doivent pointer vers le haut.

En faites comme c’est un catalyseur, j’aurais cru que le soluté A avait plus intérêt à s’accumuler dans le solide non? B (diffuser vers le bas) , que d’en sortir (diffuser vers le haut).

[LPFR]

Re.
Jusqu'à maintenant vous avez parlé de diffusion. Et la quantité de soluté (et non réactant) était constant. Si c'est toujours le cas, que ce soit un catalyseur on non cela ne change rien.

Maintenant si le soluté réagit et se transforme en autre composé, le problème n'à que peu de chose en commun avec un simple problème de diffusion. Maintenant tout diffuse et la concentration ne dépend pas uniquement de la diffusion, mais aussi du taux de réaction et de la concentration des autres réactants. Réaction avec quoi d'ailleurs?
Même si la direction générale de diffusion que j'ai donnée est encore valide, la condition limite pour y=0 n'est plus valable, car vous pouvez avoir un courant de diffusion vers une paroi étanche à cause du réactant qui se transforme près de la paroi.

Quand on pose un problème, il faut le poser complètement sans rien cacher.

A+

[Kley]

Salut Rincevent;

c'est plus raisonnable.

T’en sais quelque chose.

Je vois pas le lien entre la phrase et l'équation... "surface restante", c'est l'extérieur de la bande, pas son extrémité.


Par symetrie en y=0 tu dois avoir la même chose qu'en y=L. Mais pour moi rien n'indique cette condition dans le texte que tu cites. On peut très bien avoir un gradient nul ou ne pas en avoir, tout dépend de ce qui sépare les deux domaines...

Voila comment je vois les choses le solide B est parallélépipède rectangle : de largeur L et de longueur infinie. On a donc six surfaces : les concentrations sur les surfaces sont uniformément reparties :
-Donc la surface gauche est de concentration C₀
-La surface de base est imperméable...
Et on nous dis en faites les quatre surfaces restantes sont de concentrations nuls :
-Donc la surface de droite est de concentration nul (l’extrémité) : donc
-La surface du haut (parallèle à la base) est de concentration nul : donc
C(x,L) = 0

Voila

[Kley]

La diffusion se fait toujours des endroits plus concentrés à moins concentrés. Or zéro c'est la concentration la plus faible du monde. Donc la diffusion se fait vers la surface y=L (et vers la droite aussi, puisque la concentration al plus haute est pour x=0).

Oui, oui, tout a fait d’accord,
Ça rejoint se que j’ai dit ,et donc c’est la seul raison à l’origine de ce grad de concentration.

Jusqu'à maintenant vous avez parlé de diffusion. Et la quantité de soluté (et non réactant) était constant. Si c'est toujours le cas, que ce soit un catalyseur ou non cela ne change rien.

Ok,donc c'est ça,

Quand on pose un problème, il faut le poser complètement sans rien cacher.

Pas de soucis de ce coté (l’énoncé est au complet), c’était une question que je posais et non une information:

J’aurais cru que le soluté A avait plus intérêt à s’accumuler dans le solide non?

[invitea29d1598]

Voila comment je vois les choses le solide B est parallélépipède rectangle : de largeur L et de longueur infinie. On a donc six surfaces

déjà, tu ne donnes que 2 dimensions sur 3

on va dire que la dimension selon z importe peu ou qu'elle vaut L aussi

les concentrations sur les surfaces sont uniformément reparties :

uniformément réparties ? où lis-tu ça et que veux-tu dire par ça ?

la surface gauche est de concentration C₀

ça, c'est le seul truc sur lequel personne n'a de doute

-La surface de base est imperméable...

qu'appelles-tu "surface de base" ? si c'est y=0, alors la condition pour cette droite est probablement un gradient nul comme te le disais LPFR [en fait c'est le flux qui doit être nul si tu n'as aucune réaction à la surface, mais là, il faut plus de détails sur le catalyseur pour être fixé]

Et on nous dis en faites les quatre surfaces restantes sont de concentrations nuls

les 4 surfaces restantes, c'est quoi ? y=L, z=0 et z=L ? ça fait 3...

tu as donc une différence physique entre la "face" y=0 et la "face" y=L ? pour moi ça c'est pas clair dans ton texte mais je veux bien l'interpréter ainsi et dans ce cas je suis d'accord

-Donc la surface de droite est de concentration nul (l’extrémité) : donc

cette condition semble raisonnable mais pas nécessaire à lire ton texte car une "surface" située à l'infini n'est pas vraiment "une surface"...


ps: fausse maneouvre j'ai effacé mon message précédent auquel tu répondais

[Kley]

Je voulais revenir à cette condition LPFR , en faites tu écrits ça pour la raison que en y=0 :
la concentration est un maximum selon la variable y c’est bien cela ?

[LPFR]

Je voulais revenir à cette condition LPFR , en faites tu écrits ça pour la raison que en y=0 :
la concentration est un maximum selon la variable y c’est bien cela ?

Re.
Pour y=0, la concentration non seulement est maximale dans la direction y, mais le maximum est plat (comme les maximum d'un sinus ou d'une gaussienne). Et il est plat parce qu'une courbe de concentration non plate implique un courant de diffusion. Et, en raison de l'étanchéité, le courant (dans la direction y) pour y=0 est zéro.
A+

[Kley]

Déjà, tu ne donnes que 2 dimensions sur 3

On va dire que la dimension selon z importe peu ou qu'elle vaut L aussi

C'est exactement cela,

Uniformément réparties ? où lis-tu ça et que veux-tu dire par ça ?

Uniformément repartis, j’entendais par la que par exemple:
pour la surface gauche y C=C₀
Pour la surface droite y C=0
Pour la surface en y=L x C=0

Mais :
Par contre, pour y=0 la surface n’est pas uniformément répartis il y un gradient de concentration selon les abscisses.

qu'appelles-tu "surface de base" ? si c'est y=0, alors la condition pour cette droite est probablement un gradient nul comme te le disais LPFR [en fait c'est le flux qui doit être nul si tu n'as aucune réaction à la surface, mais là, il faut plus de détails sur le catalyseur pour être fixé]

Surface de base: y=0 on a un gradient selon les abscisses x.(grad de C décroissant vers les X>0)

les 4 surfaces restantes, c'est quoi ? y=L, z=0 et z=L ? ça fait 3...

Et x= ça fait 4

cette condition semble raisonnable mais pas nécessaire à lire ton texte car une "surface" située à l'infini n'est pas vraiment "une surface"...

Dans le texte on parle de longueur infinie, donc voila la surface droite se situe bien à x=infinie.

A+

[Kley]

Et il est plat parce qu'une courbe de concentration non plate implique un courant de diffusion. Et, en raison de l'étanchéité, le courant (dans la direction y) pour y=0 est zéro.

sincerement,j'ignorais cette notion de courbe plate!!!!
A+

[invitea29d1598]

ça me semble assez clair maintenant...

Mais :
Par contre, pour y=0 la surface n’est pas uniformément répartis il y un gradient de concentration selon les abscisses.

mais la condition physique est bien celle du flux (gradient) nul selon Y, si tu n'as pas de réaction sur cette surface.

Dans le texte on parle de longueur infinie, donc voila la surface droite se situe bien à x=infinie.

oui, oui, je comprends l'idée.... concentration nulle à l'infini semble raisonnable donc.

sincerement,j'ignorais cette notion de courbe plate!!!!

le flux est proportionnel au gradient. Donc pas de flux implique pas de gradient si le coefficient de diffusion ne s'annule pas.

[LPFR]

sincerement,j'ignorais cette notion de courbe plate!!!!
A+

Re.
Dans la frontière la concentration a une discontinuité, puisque de l'autre côté elle est égale à zéro.
Don on pourrait avoir un maximum pour y=0 avec une dérivée non nulle pour y=0 comme on les trouve dans les courbes de diffusion de chaleur. Mais ici, la paroi étanche implique que le sommet soit horizontal (derivée = 0).
C'est ce que j'ai appelé "plat", peut être à tort (mais je m'en...).
A+

[Kley]

Dans la frontière la concentration a une discontinuité, puisque de l'autre côté elle est égale à zéro.
Mais ici, la paroi étanche implique que le sommet soit horizontal (derivée = 0).

Oui,je crois comprendre:
Le Flux de diffusion selon y est donné par la premiére loi de Fick:


En y=0: la surface est étanche ce qui implique un J_y = 0 et automatiquement (Je pensais que cette notion de « plat », était une notion purement mathématique que j’ignorais)

Bien reçu : c’est plus rigoureux de dire que l’étanchéité est à l’origine de ce résultat que le fait que ce point soit juste un maximum.

[Kley]

Re.
Je viens de voir que vous allez être sérieusement emmquiquiné pour le point (0,L) qui doit satisfaire à deux conditions contradictoires. La concentration doit être C₀ et 0 simultanément!

C’est vrai, mais je pense qu’il est tout à fait raisonnable de poser C(0,L)=0 Qu’est-ce que t’en pense?

A+

[LPFR]

C’est vrai, mais je pense qu’il est tout à fait raisonnable de poser C(0,L)=0 Qu’est-ce que t’en pense?

A+

Bonjour.
Non.
Le point (0,L) est très gênant. Mais il est possible que pour le reste du problème il ne joue aucun rôle.
Le mieux, pour l'instant est de regarder de côté et faire comme si on ne l'avait pas vu. Si on peut obtenir la solution pour tous les autres points, on pourra simplement dire que la solution est valable partout sauf pour le point (0,L).
Finalement, physiquement, le problème serait le même si on passait un coup de papier de verre sur l'arête du catalyseur en faisant ainsi disparaître le point gênant.
Au revoir.

[Kley]

Finalement, physiquement, le problème serait le même si on passait un coup de papier de verre sur l'arête du catalyseur en faisant ainsi disparaître le point gênant.

Salut LPFR,
Voila,c'est pour cela que j'ai envisagé C(0,L)=0, passons le papier de verre sur ce satané point

Ok,laissons cette condition de coté;

[Kley]

Résolution mathématique:

Etant donné que le transfert est régis par un phénomène purement diffusionnel on a :



+ = 0...(1)

Je pose C(x,y) = F(x).G(y) Je remplace dans (1)

J'ai donc :.

Et je touve par la suite:
G(y) = A cos( )

et F(x) = B exp + D exp

Conditions aux limites:
1- C(+,y)= 0 => B=0,

2- => = 0,

3- C(x,L)=0 =>

4- C(0,y)=C₀ => C₀= cos(y) , Ah la je vois pas !!


En récapitulant pour l’instant j’ai :

C(x,y)= exp cos(y)

Avec :

MAIS il manque la quatriéme condition



PS:Voici le résultat au quel je dois arriver,



MAIS comment y parvenir d’où provient cette somme …. ?

A+

[LPFR]

Bonjour.
De temps en temps il faut s'arrêter de faire des maths et ne pas oublier qu'il s'agit d'un problème de physique.
Je dis cela à cause de votre égalité:

La concentration a un maximum pour y = 0. Et c'est le seul maximum qu'elle peut avoir en 'y', on ne peut pas avoir une concentration oscillante, en encore moins négative.
Donc lambda à une valeur unique

La "solution" à la quelle vous voulez arriver est simplement la somme des solutions possibles pour tous les valeurs de lambda. Simplement, l'indice de la somme utilisé est 'n' et non 'k'.
Mais c'est une solution de "matheux". Si les équations mathématiques acceptent plusieurs solutions, il se peut que physiquement ce soit possible (comme pour la vibration d'une corde de guitare), mais il se peut aussi que physiquement ce ne soit pas possible. C'est votre cas ici. La concentration ne peut être que monotone aussi bien en x qu'en y.
Au revoir.

[LPFR]

Re.
J'ai parlé un peu trop vite. La solution avec un seul lambda ne peut pas satisfaire toutes les conditions et notamment la constance pour x=0.
Il faut que je réfléchisse.
A+

[Kley]

Salut LPFR ,

Bonjour.
De temps en temps il faut s'arrêter de faire des maths et ne pas oublier qu'il s'agit d'un problème de physique.
Je dis cela à cause de votre égalité:

La concentration a un maximum pour y = 0. Et c'est le seul maximum qu'elle peut avoir en 'y', on ne peut pas avoir une concentration oscillante, en encore moins négative.
Donc lambda à une valeur unique

Je vois se que tu entend par la : 1>cos (Z)>0 se qui correspond à un Z sur [0,,dans mon exo
Z= et puisque y[0,L]
Je dois avoir : , tu as raison

MAIS il faut trouver cette fameuse expression

A priori : Avec ça on a bien C(0,y)=C₀ mais pour cela

Mais c'est une solution de "matheux". Si les équations mathématiques acceptent plusieurs solutions, il se peut que physiquement ce soit possible (comme pour la vibration d'une corde de guitare), mais il se peut aussi que physiquement ce ne soit pas possible. C'est votre cas ici. La concentration ne peut être que monotone aussi bien en x qu'en y.
Au revoir.

Donc cette solution n’est pas juste, pourtant c’est un résultat corrigé (sans démonstration).

La "solution" à la quelle vous voulez arriver est simplement la somme des solutions possibles pour tous les valeurs de lambda. Simplement, l'indice de la somme utilisé est 'n' et non 'k'.

Je peux en savoir d’avantage, car je n’ai jamais vu ça; la solution est la somme des solutions ?!!

A+

[LPFR]

Re.
Vous n'avez pas lu mon message #25 dans lequel je fais marche arrière.
Il est vrai que si une équation différentielle a plusieurs solutions, une combinaison linéaire de ces solutions est aussi une solution.
Donc, peut être que si des conditions limites ne sont pas satisfaites par une solution, peut-être qu'elles peuvent l'être pas une combinaison linéaire de solutions (je n'en suis pas sur).
Mais dans ce cas il ne faut pas imposer les conditions limites à chacune des solutions mais à la combinaison linéaire. Et c'est, peut-être, en faisant cela que l'on peut trouver les coefficients An de la combinaison linéaire:

Mais je ne suis pas sur.
A+

[Kley]

Vous n'avez pas lu mon message #25 dans lequel je fais marche arrière.

Si, je faisait que récapitulés

Il est vrai que si une équation différentielle a plusieurs solutions, une combinaison linéaire de ces solutions est aussi une solution.

Ok,dans note cas :chacune des solution particuliéres est de la forme

Donc, peut être que si des conditions limites ne sont pas satisfaites par une solution, peut-être qu'elles peuvent l'être pas une combinaison linéaire de solutions (je n'en suis pas sur).

C’est intéressant, ça pourrait expliqué? le pourquoi de la forme de se résultat,

Et c'est, peut-être, en faisant cela que l'on peut trouver les coefficients An de la combinaison linéaire:

J’espère qu’on pourra nous le confirmer …

A+