Bonsoir,
j'ai besoin d'aide, je ne sais pas comment faire lorsque la paroi du barrage est une courbe, quelle formule utilisée pour répondre à cette question. J'espère que quelqu'un pourra m'aider, merci d'avance.
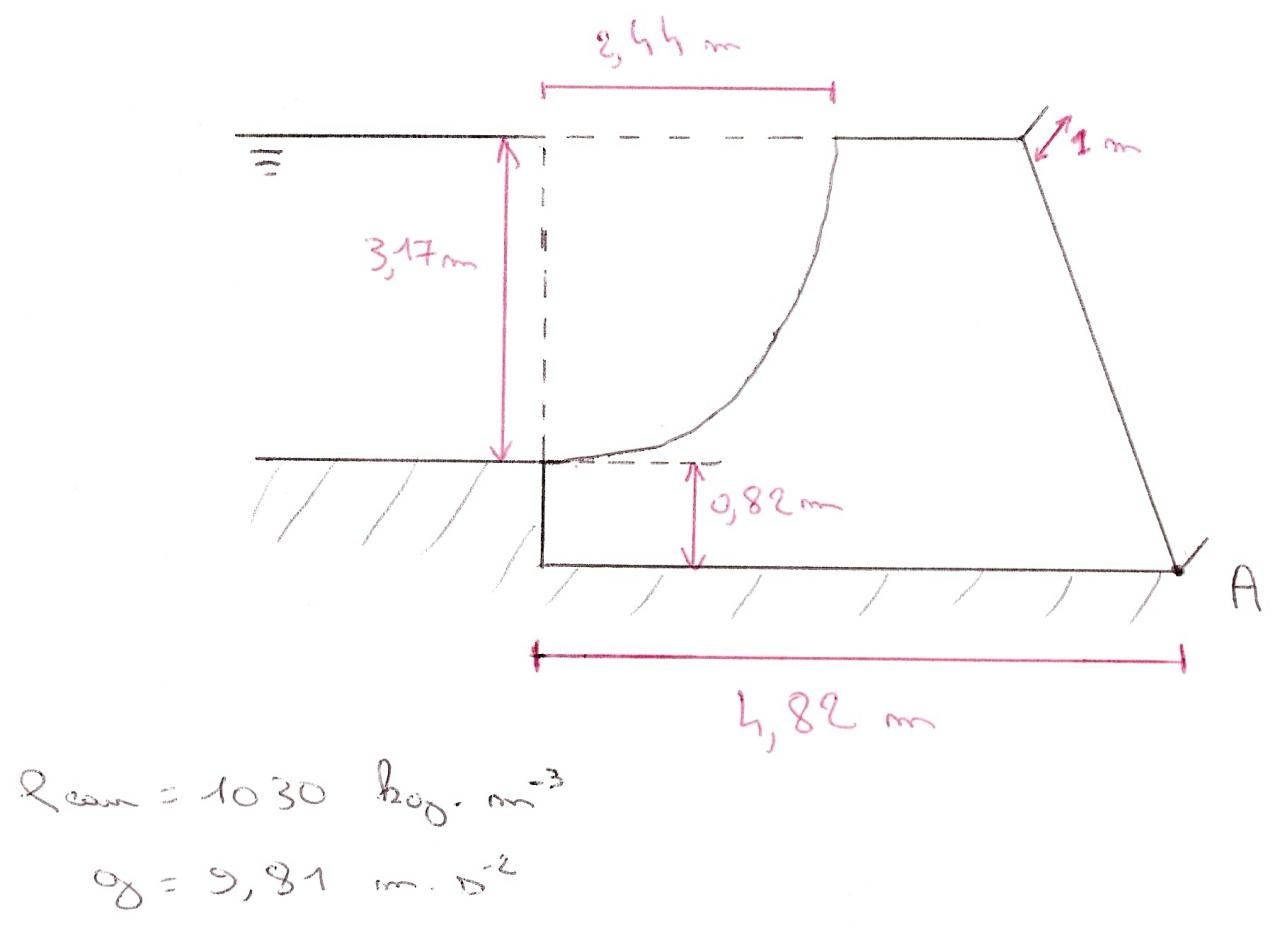
calculer le moment en A du à l'action du volume d'eau sur le barrage.
Bonsoir.
Le fait que ton barrage soit courbe ne change en rien le raisonnement global qui serait utilisé pour un barrage plan (écriture de la "force élémentaire" puis intégration sur la surface du barrage).
La seule chose qui va changer ici est que la normale au barrage va dépendre du point auquel tu calcule la "force élémentaire"...l'intégration va être un peu plus ardue mais en explicitant bien les termes, on y arrive.
Quelle est exactement la forme du barrage (arc de cercle?)
Désolé pour la fote dortograf
calculesauquel tu calcule la
noon il y a aucun probléme, au contraire je me sentiré plus a l'aise, sinon moi aussi je vais chercher à pas faire de faute ce qui est pas possible.
c'est une parabole.
moi je m'étais dit qu'il falait calculer le poid de l'eau, puis chercher le centre de poussé sur l'axe y puis sur l'axe x. mais je sais pas comment faire pour calculer la force dans ce genre de barrage ( sur un barrage plan je saurais le faire, F= ROg(hg)S ) mais là j'ai aucune idée.
Je ne vois pas trop l'intérêt de passer par le centre de poussée.
On te demande de calculer le moment en A (d'ailleurs qui est A, je n'est pas accès à ta pièce jointe), donc calculons le de par sa définition :
où
et lorsque l'on intègre sur toute la surface du barrage
Tu connais la valeur de la pression en fonction de la profondeur et il te reste à déterminer les expressions de dS et de cette normale via la géométrie du barrage
Oh la vache!!!je n'est pas accès à ta pièce jointe
je n'AI pas....
bah moi c'est la première que je fais de la mécanique des fluides et on a pas vu d'exo avec des intégrations. on les résout seulement en utilisant la formule de la force et les centres de poussé.
j'aimerais te faire voir le schéma. tu peux me dire comment faire ( c'est la première que j'utilise ce site ). merci beaucoup
Nan c'est bon je peux le visualiser maintenant mais j'avoue que je capte pas trop la situation. Enfin peu importe.
Tu évoques une formule avec le centre de poussée mais je ne vois pas à quoi tu fais allusion.
Sinon, tes difficultés ne résident pas dans le mécanique des fluides (d'ailleurs ce n'en est pas vraiment) mais plutôt dans le formalisme mathématique du moment d'un effort sur un solide.
Tente de voir si tu ne peux pas trouver de résolutions faisant appel à cette définition du moment.
Bon courage.
Ah ça y est j'ai pige ton shéma.
Le barrage est incurvé de profil mais vu de haut, il ne présente aucune courbure, c'est bien ça?
non il é courbé là où il y à l'eau. de tout façon faut pas le voir du haut.
Cela changerait quand-même pas mal de choses si le barrage était "courbé vu de haut".
Enfin bref.
Donc je te propose de décomposer la surface en contact avec l'eau en une infinité de tranches horizontales.
Essaie de voir ce que tu peux faire avec ça...
oui il est courbé vu de haut. tu ne crois pas que , en calculant le centre poussé appliqué sur le plan yz et celui appliqué sur xy et en calculant les forces qui s'y applique , on puisse en déduit le moment en A (on a les distances)
Certes mais par définition le centre de poussée est le point où la moment est nul.
Donc pour le déterminer il faut calculer le moment en un point P quelconque et ensuite trouver P tel que cette quantité soit nulle.
Donc autant déterminer directement le moment en A, non?
A moins que tu ne connaisses une relation qui te donne facilement la position de ce fameux centre de poussée auquel cas je suis preneur.
PS : je comprend plus dans le post #10 tu dis que le barrage n'est pas courbé vu de dessus et là tu me dis le contraire. Alors courbé vu de haut ou pas? (A mon avis non, il est juste courbé de profil)
la formule pour le centre de poussé c'est hcp= Iyz/((Yg)(S))+Yg. je disé ça parce que je savé pas ce que tu voulais dir par vu d'en haut. pour moi si c'est courbé de profil c'est forcement courbé vu d'en haut.
?????????????????????????????? ???????????????hcp= Iyz/((Yg)(S))+Yg
Tu peux dire qui correspond à quoi stp?
Par contre je dois m'absenter.
Je reviens d'ici une demi-heure
A toute'
ça sa marche quand le barrage est plan. Iyz centre d'inertie divisé par le cente de gravité fois la surface + le centre de gravité ça donne le centre poussé.
Re.
Alors effectivement ce que tu as écrit fonctionne pour une surface plane mais je pense que cette formule provient de la démarche que je te propose.
Je rappèle en effet que la définition intrinsèque du produit d'inertie est:
Du coup, à mon avis, ta formule provient du fait que lorsque tu écrit le moment sous forme intégrale dans le cadre d'une plaque plane, le terme intégral Iyz apparaît de lui-même...
Mais ici, on ne peut appliquer cette relation, il faut donc revenir au cas général en passant par la définition du moment mais ça je l'ai déjà évoqué plus haut...
B'jour,
Si on veut rester dans une formulation simple, on fait par les composantes horiz et vert de la poussée.
On peut intégrer pour la poussée horiz ou poser direct F=rho g h²/2, le résultat devant être connu par cœur au bout d'un moment. Idem pour la position dont on connaît la position à h/3.
Pour la poussée vert et sa position, faut intégrer.
On peut aussi faire sans aucune intégrale si on connaît quelques trucs à condition que l'origine de la parabole soit son sommet, ce qui semble être le cas ici.
Mais si t'as l'gosier, Qu'une armure d'acier, Matelasse. Brassens, Le bistrot.
donc il faut considérer qu'il y a deux forces qui s'applique sur le barrage, une horizontale qui s'applique à 3.17/3 puis une verticale qui s'applique à 2.44/3.Envoyé par sitalgo
alors la force horizontale c'est F= 1030x9.81x(3.17/2)x(3.17x1)
par contre la force verticale je ne vois pas comment la calculer.
puis quand on a c'est force on sait qu'elle s'applique sur le centre de poussé qu'on a calculé. puis on cherche le moment en A.
c'est ça ??
Ah ben oui.
Ah ben non.puis une verticale qui s'applique à 2.44/3.
On peut appliquer rho g h²/2 et h/3 parce la variation de pression rhogz est linéaire selon z, mais pour la force verticale il faut intégrer en fonction de la hauteur d'eau selon x.
Une fois que tu as la force tu peux trouver sa distance par les moments : F d = Somme(dF x)
La décomposition est bizarre, si on n'intègre pas il s'agit de trouver la surface d'un triangle, on a rhogh la base, h la hauteur, ça donne un rectangle, et 1/2 pour la surface du triangle.alors la force horizontale c'est F= 1030x9.81x(3.17/2)x(3.17x1)
Mais si t'as l'gosier, Qu'une armure d'acier, Matelasse. Brassens, Le bistrot.
mais la paroi du barage est une parabole. pour intégré sur x il faut que je prennes y=x^2 , non ? et l'intégration ça donne quoi ??
"barrage", "intégrer" et "je prenne" dsl pour l'ortographe
Voilà, il faut trouver l'équation de la parabole, considère l'origine du repère Oxz au point bas de la parabole, ça facilite les choses.
Mais si t'as l'gosier, Qu'une armure d'acier, Matelasse. Brassens, Le bistrot.
C'est bon.
Ce n'est pas bonne équation, c'est en y = ax², il faut que y=3,17 pour x=2,44.pour Fy j'ai intégré en prenant y=x^2
Non. Quelle est ton équation d'intégrale au départ? Ca doit coincer là. Ici il n'apparaît pas 3,17 ni un coef qui le remplacerait.soit Fy=1030x9.81x1x[2.44^3/3]=48927.6 N.
Regarde mon message plus haut.le centre de poussé de cette force je n'arrive pas a la trouvé ( enfin je c'est pas comment faire ) si tu pouvé me dire comment tu fais et combien ça donne, je saurais trouver le moment en A.
Mais si t'as l'gosier, Qu'une armure d'acier, Matelasse. Brassens, Le bistrot.
pour Fy=ro.g.L. intégrale ( 0 ; 2.44) y dx
( dsl je ne sais pas comment dessiner les intégrales et les bornes c'est de 0 à 2.44 ) c'est bon pour la formule ??
donc avec y=ax^2 on a un coefficient directeur de 0.53.
si c'est ça alors Fy=25931.6N
Somme de y dx donne la surface sous la parabole, il faut trouver la surface au-dessus (entre la surface de l'eau et le sol).
Oui.donc avec y=ax^2 on a un coefficient directeur de 0.53.
Mais si t'as l'gosier, Qu'une armure d'acier, Matelasse. Brassens, Le bistrot.
ah alors il faudrait faire Fy=ro.g.L. intégrale ( 0 ; 2.44) y.dx.dy ??
Il te faut trouver la somme des tranches d'eau verticales d'épaisseur dx et de hauteur h(x), donc F=rhog S(h(x)dx). La fonction h(x) est facile à trouver.
Le S est le signe intégrale.
Mais si t'as l'gosier, Qu'une armure d'acier, Matelasse. Brassens, Le bistrot.
Histoire de répéter ce qui est sur l'autre fil : la force sur la paroi plane vaut rho g L H²/2 et elle est appliquée aux 2/3 en partant du haut.
La force sur la paroi courbe + la force sur la paroi plane ont pour effet de contrebalancer le poids de l'eau entre les parois.
Donc la force sur la paroi courbe a une composante horizontale égale à rgo g L H²/2 et une composante verticale rho g V où V est le volume (pas trop dur à calculer).
Si on regarde le point à la verticale de G à 2/3 en partant du haut, on voit que la force F et le poids G ont un moment nul par rapport à ce point donc la force sur la paroi courbe aussi.
Pas d'intégrale curviligne ni d'intégrale double, ça se fait de tête.
