J'ai l'equivalence suivante que je veux démontrer mais j'arrive pas puisque en première année on est pas formé suffisamment dans les opérateurs différentielles
E est un le vecteur du champ magnetique et V est le potentiel électrique , j'arrive biensur à arriver à la relation suivante entre les deux .
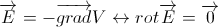
Car V est un scalaire son rotationel est nul.
Par definition^il sagit du produit scalaire (.) et du produit vectoriel(*)
rot E=div * E
Bonjour.
Je vous copie cette règle de la charte de ce forum:
Au revoir.2. La courtoisie est de rigueur sur ce forum : pour une demande de renseignements bonjour et merci devraient être des automatismes. Vous pouvez critiquer les idées, mais pas les personnes.
Merci beaucoup !
Prochaine fois j'y tacherai de respecter la charte
Re.
Il faut que vous démontriez que le rotationnel d'un gradient est toujours nul.
"Yaka": il faut écrire le gradient d'une fonction quelconque, et calculer son rotationnel.
Puis trouver les termes qui s'annulent par paires.
L'astuce est que les dérivées partielles, en physique classique, sont permutables:
A+
Bonjour, ne faut-il pas démontrer aussi la réciproque ? C'est-à-dire que si son rotationnel est nul, alors le champ de vecteur est un gradient.Envoyé par LPFR
Vous dites en physique classique car vous faites référence à la continuité ? (normalement l'égalité est valable pour une fonction C^2, je crois...)
Je crois qu'il fait référence à la commutation
Re.
Pour démontrer l'inverse, qu'un champ irrotationnel dérive d'un potentiel, on ne peut pas le faire "yaka". Je ne souviens plus de ce qu'il faut faire. Je ne sais pas si passer par Stokes suffit.
Je crois qu'en mécanique quantique on trouve des opérateurs non permutables (non Hermitiques si je ne me trompe pas). J'ai ajouté "classique" pour éviter que l'on parte dans les maths. En physique classique, toutes les fonctions son sages et infiniment dérivables, etc., etc.
A+
Bonjour, je suis d'accord pour les opérateurs, même si je ne vois pas ce que ça change pour des dérivées partielles, puisqu'elles ne changent pas de nature si on passe à la physique quantique.
Sinon, j'ai trouvé une démonstration (ou peut-être une ébauche de démonstration car ce n'est pas ultra mathématique et suppose qu'on a déjà défini le potentiel) dans le livre de Feynman.
"Considérons deux points, l'un en x et l'autre en (x+dx), mais tous deux ayant le même y et le même z, et cherchons quel travail on effectue quand on transporte une charge unitaire du premier point à l'autre. Le trajet se fait le long de la ligne horizontale de x à jusqu'à x+dx. Le travail effectué est la différence de potentiel entre les deux points :
Mais le travail effectué contre le champ pour le même trajet est [il a expliqué auparavant qu'il était indépendant du chemin suivi]
On voit que
De même,,
