principe d'un éléctromètre : maths spé

[invite7b59b99d]

Bonsoir!

J'aimerai avoir un peu d'aide au sujet d'un problème assez difficile a mon sens en éléctromagnétisme, dont voici l'énoncé :

tous les dispositifs seront placés dans le vide.

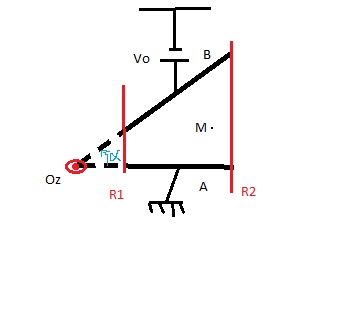
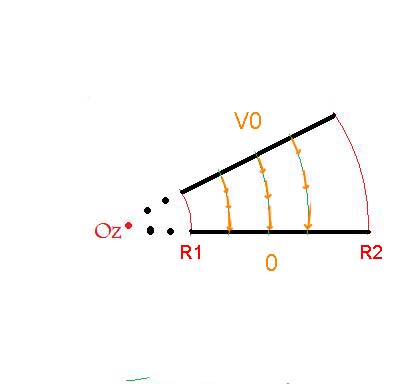
1) on considère un condensateur dont les 2 armatures A et B sont rectangulaires et sont situées dans deux plans verticaux faisant entre eux un angle . Les cotés verticaux de ces rectangles, de hauteur h, sont respectivement situés aux distances R1 et R2 de la droite commune (l'axe Oz) à ces 2 plans.



1.1 Ces deux armatures étant respectivement portées aux potentiels Va=0 et Vb=V0, quel est le potentiel V(M) en tout point M de coordonnées cylindriques r,theta,z situé entre les armatures? on néglige tout effet de bord et on rappelle la valeur du laplacien en coordonnées cylindriques. (voir formule : http://www.google.fr/imgres?q=laplac...t:429,r:1,s:85 )

déja pour cette première question, puis-je utiliser directement la formule de poisson, vu que je suis "dans le vide" et si je suppose les armatures a l'équilibre? si oui, comment puis-je exprimer la densité volumique de charges?

Merci d'avance aux courageux!
-----

[LPFR]

Bonjour et bienvenu au forum.
Vous êtes dans le vide: il n'y a pas de densité volumique de charges. Elle est zéro.
Les charges sont à la surface des armatures et du côté interne.
Et j'imagine que la petite phrase "on néglige les effets de bord", vous invite à supposer que le champ est tangentiel en tout point (perpendiculaire à 'r' et à 'z'). Cela vous permet de calculer le champ électrique en fonction du rayon et, à partir de là, la charge de surface (aussi en fonction de 'r').
Au revoir.

[invite7b59b99d]

Merci pour votre aide! Je vais essayer de faire ça comme vous l'indiquez...(j'avais écarté le calcul de champ, faute de symétries flagrantes dans le système...)

[invite7b59b99d]

Par contre, en passant par E=-grad(V), je trouve que V(r)=E*r*alpha (angle, que je n'ai pas nommé dans l'énoncé, entre les 2 armatures)
Je ne vois pas ou je dois utiliser la formule du gradient ni comment calculer le champ electrique (puisque la densité volumique de charge est nul, à part dire que celui-ci vaut la densité surfacique de charge divisé par la permitivité du vide à la surface des armatures, je ne vois pas...)
Merci

[A voir en vidéo sur Futura]

[LPFR]

Bonjour.
Pour avoir du champ à un endroit donné, on n'a pas besoin qu'il y ait des charges à cet endroit. Une charge ponctuelle crée du champ dans tout l'univers. Et le champ crée obéit à div E = 0 et à Laplacien de Phi = 0 partout sauf dans la position de la charge.
Donc, l'équation qui décrit votre problème est Laplacien de Phi = 0. Mais vous savez que des termes de ce Laplacien sont nuls par symétrie et par la supposition de l'absence d'effets de bord.
Ça veut dire que dans la formule que vous donnez en lien, le second et le troisième terme sont nuls.
Votre formule V(r)=E*r*alpha n'est pas mauvaise si vous l'interprétez correctement, car au niveau des armatures le potentiel ne dépend pas de 'r'. En fait, ce qu'il faut que vous trouviez c'est E en fonction de 'r'.
Au revoir.

[invite7b59b99d]

Déja, merci LPFR!
Alors si j'ai bien compris, comme div(E)=0 (car pas de densité volumique de charges entre les plaques), on a div(-grad(V))=0 donc le laplacien de V est nul.
Maintenant il reste toujours deux choses qui me bloquent :
*pour calculer E en fonction de r, je ne dois prendre en compte que la plaque B si je ne m'abuse (car son potentiel est non nul égal à V0) mais comment procéder? tout ce que je sais, c'est que E sera selon le vecteur u(theta) mais je ne vois absolument pas comment le déterminer.
*pour le laplacien, je ne vois pas pourquoi les termes s'annulent, car justement je ne vois pas les symétries!

Merci beaucoup pour votre aide.

[invite7b59b99d]

Voila un dessin de la situation.

[LPFR]

Bonjour.
Faites un dessin.
Dessinez des arcs de cercle entre les deux plaques.
Les lignes de champ suivent ces arcs de cercle.
La différence de potentiel entre les deux plaques est égale à l'intégrale de ligne de E le long des lignes de champ.
Ou, même chose, vous partez de votre formule V(r)=E*r*alpha et sortez la valeur du champ:
E = (V1 - V2)/(alpha*r).
et (V1 - V2) est la différence de potentiel entre les plaques.

Je vous conseille de lire ce petit fascicule:
http://forums.futura-sciences.com/at...aire-nabla.pdf
et vous comprendrez pourquoi le Laplacien s'annule là où il n'y a pas, des charges.
Au revoir.

[invite7b59b99d]

Merci!
J'ai bien le résultat E=-V0/(r*alpha)
Pourquoi ne puis-je pas simplement dire que le potentiel entre le plaques est de E*r plutot que de passer par le Laplacien (la seule dérivée qu'il nous reste ici est par rapport à r, et si je ne m'abuse, V=V0/alpha et il ne reste plus rien à dériver en r...)?
Dois-je dire que la solution générale de (1/r)(d/dr)(r*(dV/dr)) est de la forme V=A/R+B? cette forme de résolution ne me semble pas correspondre...

[LPFR]

Bonjour.
Votre dessin a été validé. Il est mauvais.
Les deux armatures ont la même largeur: leurs extrémités se trouvent sur les mêmes cercles à R1 et R2. Relisez l'énoncé "Les cotés verticaux de ces rectangles, de hauteur h, sont respectivement situés aux distances R1 et R2 de la droite commune (l'axe Oz) à ces 2 plans."

Et non. V ne peut pas dépendre de 'r' car au niveau des armatures V est constant de R1 à R2.
Faites le dessin correctement et dessinez E le long des lignes de champ.
Au revoir.

[invite7b59b99d]

j'ai corrigé mon dessin pour y voir plus clair.

Mon problème est que, vu que l'on est parvenus a déterminer E et V sans le laplacien ici, a quoi cela sert d'en donner la formule a cet endroit de l'énoncé? On dit juste que, comme 2 des 3 termes s'annulent par symétrie (comme vous l'aviez mentionné) et que l'autre s'annule aussi car on a vu que V ne dépend pas de r, alors V vérifie bien Laplacien V=0?

Cela ne sert pourtant probablement pas à la deuxième question : "en déduire la capacité C1 de ce condensateur en fonction de alpha, h, R1 et R2."

[invite7b59b99d]

avec les flèches jaunes la représentation du champ electrique, qui descend les potentiels.

[LPFR]

Bonjour.
Cette fois je suis d'accord avec votre dessin. Il est très bien.
Et aussi avec vos conclusions.
Quant à l'utilité du Laplacien j'avais attribué ça à "math sup" qui aurait tendance à faire plus de maths que de physique. Moi aussi je le trouve inutile dans ce problème.

Maintenant, vous connaissez le champ électrique sur les plaques. Vous pouvez donc calculer la densité de charge de surface (E = sigma/epsilonz). Donc, vous pouvez calculer la charge totale sur chaque plaque. Et comme vous connaissez la différence de potentiel entre les plaques, vous pouvez déduire la capacité.
Au revoir.

[invite7b59b99d]

D'ailleurs ne serais-ce pas plutôt le deuxième terme du Laplacien qui serait non nul par symétrie?
Et une dernière question "bête" en partant d'un autre point de vue : vu qu'il n'y a pas de charges entre les deux plaques, ne peut-on pas considérer le champ E nul entre les 2 plaques? Merci en touts cas!

[LPFR]

D'ailleurs ne serais-ce pas plutôt le deuxième terme du Laplacien qui serait non nul par symétrie?
Et une dernière question "bête" en partant d'un autre point de vue : vu qu'il n'y a pas de charges entre les deux plaques, ne peut-on pas considérer le champ E nul entre les 2 plaques? Merci en touts cas!

Bonjour.
J'ai l'impression que vous n'avez pas lu mes réponses et que cet exercice ne vous a servi a rien.
Et tout cas, c'est ce que vous deux questions semblent dire.
Au revoir.

[invite7b59b99d]

C'est juste que j'essaye de comprendre en quoi il peut etre utile d'employer le Laplacien...j'avais bien prévenu que les question seraient "bêtes", mais j'aimerai bien pouvoir retrouver mon résultat en utilisant le Laplacien. (question d'assurance)
J'ai parfaitement lu vos réponses et j'en ai pour preuve que je suis parvenu à un résultat cohérent avec ce que vous expliquiez.

[invite7b59b99d]

La différence de potentiel entre les deux plaques est égale à l'intégrale de ligne de E le long des lignes de champ.
Ou, même chose, vous partez de votre formule V(r)=E*r*alpha et sortez la valeur du champ:
E = (V1 - V2)/(alpha*r).
et (V1 - V2) est la différence de potentiel entre les plaques.

Désolé, j'ai en effet répété l'une de mes questions (ceci du au fait que je suis sur cet exo de manière un peu intermittentes depuis une semaine, et que je travaille beaucoup d'autres sujets en meme temps, j'ai donc un peu perdu le fil...)J'ai bien relu notre conversation, et quelque chose m'intrigue : j'ai trouvé ma formule de V en utilisant E=-gradV. Mais en fait cela revient exactement a ce que vous me proposiez prime abord, en me disant de calculer l'intégrale de E sur les lignes de champ.
Du coup, on a pas "d'indépendance" entre notre calcul de E et de V, je ne puis que donner E en fonction de V et V en fonction de E. Comment puis-je avoir simplement, par exemple E en fonction de r seulement, comme vous me le suggériez? Par exemple, Gauss sur la palque B suffit-il?
Merci.

[LPFR]

Bonjour.
E et V ne sont pas indépendants puisqu'ils sont liés par E = - grad V.
Par contre, à un endroit donné, E ne dépend que de l'endroit et de la différence de potentiel entre les deux plaques. La formule E = (V1 - V2)/(alpha*r) est ce que vous cherchez. Le module de E ne dépend que de 'r' et sa direction est toujours tangentielle et V ne dépend que de thêta.
Au revoir.

[invite7b59b99d]

Je vois.
Merci pour votre aide tout au long de cette discussion.