Force de pression sur une sphere de rayon a=Force de pression sur un disque de rayon a

[yootenhaiem]

Bonsoir,
Voila je travaillais un exo sur les ondes em, et on a parle de photons et de quantite de mouvement.
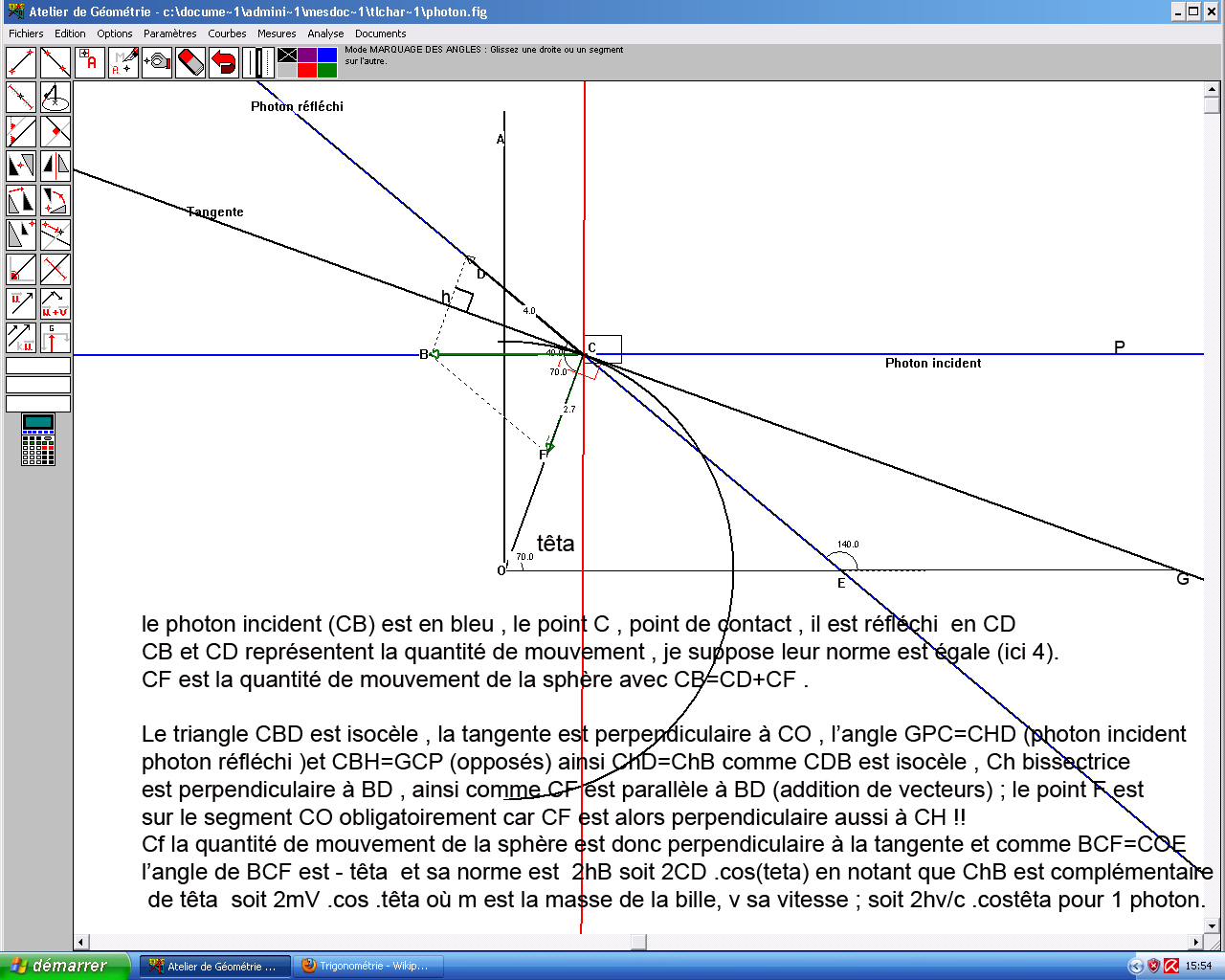
On bombarde une sphere réfléchissantede rayon a par des paquets de photons. On nous demande de trouver la force exercee sur la sphere par les photons. C'est bien proportionnel a leur quantite de mouvement. Mais en remarquant que laquantite de mouvement est moins importante dans une sphère vu l'angle de choc, je me suis dis que la force serait inférieur a celle d'un disque orthogonalement posee devant les trains d'onde. Or, c'est la même valeur.Autrement, A quoi bon l’aérodynamique.
-----

[LPFR]

Bonjour.
Non. Ce n'est pas la même chose dans le cas d'objets réfléchissants que dans le cas d'objets absorbants. Et ça fait même une différence entre un miroir et une feuille blanche.
Il est vrai que les photons n'ont rien à foutre de l'aérodynamique. Ils ne savent même pas que cela existe. Mais à leur décharge, ils ne se comportent pas ni comme un fluide ni comme des molécules. Ils peuvent passer les uns à travers les autres sans même se dire bonjour. Ce que les molécules ne savent pas faire.
Au revoir.

[yootenhaiem]

donc j’écris que les photons sont mal polis?
En fait, j'ai considéré un infiniment petit est j'ai vu que la quantité de mouvement était proportionnelle a l'angle ou se situe le point de contact. Mais lorsque le photon entre en choc avec la demi-sphère(dans ce cas absorbante), sa quantité de mouvement est la même reçue par la sphère? ou faut il faire intervenir les angles, et projeter après sur l'axe voulu.

[yootenhaiem]

Voici mes calculs LPFR:

On remarque que si l'on se mettait face a face avec la sphere de telle facon que les photons venaient de derriere nous, on aurait une invariance selon la rotation d'angle par rapport a , et une dépendance de la distance du point d'impact avec l'axe . On voit que l'impact premier est le meme pour une absorption du photon, apres il y'a reflechissement et donc le photon se remet en mouvement et redonne donc une quantite de mouvement supplementaire a la sphere:
La quantité de mvt du photon:
La quantité de mvt au voisinage d'un point repéré par en coordonnées sphérique,et selon le vecteur :
; ou x est la projection de r sur l'axe
D'ou
On en deduit en integrant: .

C'est juste?

[A voir en vidéo sur Futura]

[yootenhaiem]

Voici mes calculs LPFR:

On remarque que si l'on se mettait face a face avec la sphere de telle facon que les photons venaient de derriere nous, on aurait une invariance selon la rotation d'angle par rapport a , et une dépendance de la distance du point d'impact avec l'axe . On voit que l'impact premier est le meme pour une absorption du photon, apres il y'a reflechissement et donc le photon se remet en mouvement et redonne donc une quantite de mouvement supplementaire a la sphere:
La quantité de mvt du photon:
La quantité de mvt au voisinage d'un point repéré par en coordonnées sphérique,et selon le vecteur :
; ou x est la projection de r sur l'axe
D'ou
On en deduit en integrant: .

C'est juste?

Ce raisonnement est-il juste SVP?

[yootenhaiem]

Alors les gens?

[triall]

Bonjour, les calculs m'intéressent , mais peut -on avoir un petit dessin avec l'axe Ox , le vecteur Ux ....

[shiv]

Bonsoir,

Sans prendre le temps de comprendre tous les calculs, mais pour revenir sur l'interrogation première, la quantité de mouvement est moins grande à chaque choc, mais il y a plus de chocs puisque la surface de contact est plus grande. En fait, le même flux intercepte un disque et une sphère si elle ont même rayons.

[triall]

Bonsoir,

Sans prendre le temps de comprendre tous les calculs, mais pour revenir sur l'interrogation première, la quantité de mouvement est moins grande à chaque choc, mais il y a plus de chocs puisque la surface de contact est plus grande. En fait, le même flux intercepte un disque et une sphère si elle ont même rayons.

Bonsoir, il me semble que les photons sont parallèles entre eux, et qu'il y a autant de chocs, non ?

[shiv]

Hum... si les photons sont bien des particules discrètes, et qu'on veut compter les chocs, triall, tu as peut-être raison. En tout cas, je crois qu'on a tous en tête une sorte de ligne de photons bien rangés en rang d'oignons, prêts à aller s'écraser sur leurs cible, chacun voyageant en ligne droite. Mais si la distance entre les concurrents sur la ligne de départ tend vers 0, on retombe dans le cas continue. Et si les photons suivants (on a un flux) ont des starting-blocs décalés n'importe comment par rapport à leur prédécesseurs, je ... conjecture qu'on retombe dans le cas continue.

Je ne sais pas bien les limites de validités de mon raisonnement, mais pour ce qui est du calcul, quand on fait l'intégrale, le flux de photons est représenté par le même objet abstrait qu'un flux de fluide/champ classique, on est donc dans un cas continu et non discret

[albanxiii]

Bonjour,

En fait, le même flux intercepte un disque et une sphère si elle ont même rayons.

Et vous ne tenez pas compte de l'angle entre la trajectoire du photon incident et la normale de la surface où il tape ?

[yootenhaiem]

Oui bien sur j'ai voulu calculer la quantité de mouvement reçue selon l'axe (Ox), pour pouvoir calculer après la force exerce par les photons sur la paroi sphérique.Le phenomene est claire, ce sont les calculs qui m’intéressent

[yootenhaiem]

oui Shiv, la surface est plus grande mais en chaque point la quantité de mouvement reçue est moins grande car il y'a déviation de la trajectoire, non stoppage+retournement(comme le cas des surfaces planes). Aussi j'ai pris en considération la surface de contact avec les photons.
La question de flux est importante, il y'a égalité dans le cas d'une sphère et d'un disque , mais la quantité de mouvement reçue est moindre plus on s'approche des pôles.

[yootenhaiem]

Mais bon physiquement parlant on ne s’arrêtera jamais. <3 Physics <3
Du coup on doit voir les calculs d'abord; mes calculs, puis les vôtres.

[triall]

Bonsoir, oui mais 2ème tentative, peut-on avoir un schéma pour savoir où est OX ?.....

[yootenhaiem]

Bon voila un petit schema.

[LPFR]

Bonjour.
Premièrement il faut que vous vous décidiez: les photons sont-ils:
- absorbés
- réfléchis spéculairement
- réfléchis de façon diffuse (dans toutes les directions possibles).

Faites un dessin de la coupe, et calculez la variation du moment des photons dans la direction incidente, après réflexion (ou absorption), en fonction de l'angle de contact (thêta) avec la sphère.
Le calcul est nettement plus long si la réflexion est diffuse.
Faites un dessin en 3 dimensions.
Dessinez un ruban de largeur correspondante à d(thêta). Calculez la surface apparente présentée aux photons par ce ruban. Calculez le nombre de photons par unité de temps qui frappent au niveau du ruban. Calculez le changement de moment sur le ruban. Intégrez sur la surface de la sphère.
Au revoir.

[shiv]

Bonjour,

Grâce à LPFR je reviens sur ce que j'ai dit. Je raisonnais comme si les photons étaient absorbés pour dire que comme on avait les même flux de quantité de mouvement, on devait avoir la même pression. Mais si on a une réflexion, spéculaire ou diffuse, la pression doit être différente entre le cas d'un plan et le cas d'une sphère je pense. Je ne fais pas avancer le schmilblick, mais je tenais à me corriger.

Un plan incliné à 45° reçoit la moitié de la quantité de mouvement lorsqu'un photon le frappe avec réflexion "à la Descartes" par rapport à un plan vertical (les photons voyageant horizontalement). Mais la surface est racine de 2 fois plus grande. D'où un rapport 2 sur racine de 2 entre les deux géométries. Bon courage.

[yootenhaiem]

Si les photons etaient absorbes, on ne considererait que le flux des photons a travers un disque de meme rayon que la sphere.
Ici ils sont parfaitement reflechis. tq le vecteur de vitesse d'avant le choc, la normale a la sphere en le point de chox, et le veteur de vitesse du photon reflechis sont dans le meme plan.

[triall]

Bonsoir donkishot, j'ai un niveau moins élevé que vous , très certainement, justement, quand vous vous exprimez , ayez des redondances en explications, ce qui est clair pour vous ne l'est pas forcément pour l'interlocuteur ; d'autant que les fautes d'orthographe et pire de grammaire rendent le "discours confus" .De plus , employer des abréviations comme "tq" sont en dehors de la charte, je ne comprends pas ce que cela signifie ...
Faites un effort en communication , cela vous obligera à poster un écrit clair , et faire ainsi un travail sur ce que vous voulez exprimer , et vous aidera à mettre vos idées au clair pour bien les faire comprendre aux autres et à vous même . Ne bâclez pas vos dessins (merci tout de même pour l'effort, mais il me semble que l'angle i est mal placé !!)

Bonne soirée.

[triall]

Bonsoir, on aurait pu s'en douter , mais en traitant le photon comme une bille qui rebondit élastiquement, et en faisant l'approximation que la quantité de mouvement de la bille réfléchie est la même en norme , je trouve que la quantité de mouvement de la sphère est donnée par le vecteur
perpendiculaire à la tangente du point d'impact, d'angle - têta et de norme 2mv.cos.têta , têta étant l'angle qui donne la position de l'impact sur la sphère : 0° pour un impact dans l'axe , 90° pour un impact tangent , m la masse de la bille v sa vitesse .Pour un photon on remplace mv par hv/c , h constante de Planck , v fréquence du photon .
Ce résultat est remarquable, après l'impact, la sphère file en direction de son centre donc en fait .
J'ai fait aussi la démo analytique .
A noter qu'en réalité le photon, ou la bille perdent un peu de quantité de mouvement (en norme) , le photon en diminuant sa fréquence, la bille sa vitesse . la démo géométrique est là

[yootenhaiem]

Bonsoir Triall,
J’apprécie tellement votre honnêteté et votre charisme. Je dois avouer que j’écris précipitamment et que surviennent alors les fautes que vous avez citées plus haut, ce qui leurre mes explications, et les rend ambiguës et dénuées de sens même.
Je dois dire aussi que votre interprétation physique concernant l'impact du photon et de la sphère, et de la modélisation d'une bille qui rebondit, est la même chez moi. Cependant, mon problème réside en le calcul de la quantité de mouvement reçue par toute la demi sphère. Il est donc question de calculer la quantité de mouvement dans une portion de la sphère , et de faire intervenir l'angle "i" et la distance "x", ainsi que les variation "dx" et "di" et ce dans le but d’intégrer par la suite: d'obtenir la quantité de mouvement sur toute la surface ou retentissent les photons.

[triall]

Bonsoir, j'ai une bonne formation et de bons restes en géométrie euclidienne; mais pour ce qui est d'intégrer , j'aimerais faire des progrès ....
Merci pour les appréciations peu méritées, je crois .
J'ai fait rebondir une bille sur un cylindre en fait , et le résultat obtenu , avec l'approximation M masse de la sphère grande par rapport à m masse de la bille me semble bonne et très vraisemblable , avec la norme de la vitesse de la bille incidente égale à la norme de la vitesse de la bille réfléchie .

La suite en 3 d me semble logique, mais je n'ai pas pour l'instant la démonstration :
Ce "doit" être pour la norme du vecteur quantité de mouvement de la sphère MV2 =2mvcostêta.cos.alpha , et la direction de ce vecteur toujours évidemment le centre de la sphère . M masse de la sphère V2 sa vitesse en norme , m masse de la bille et têta et alpha coordonnées polaires ....
têta étant l'angle polaire du dessin , alpha l'autre angle d'Euler .(azimut -ascension droite)
Je n'ai pas la démonstration pour alpha , pour l'instant ,mais peut-être quelqu'un ?

Il faudrait donc avoir comme l 'écrit LPFR la densité de photons par surface(apparente) par seconde et intégrer je ne sais trop comment .... pour avoir la force donnée par les photons sur cette sphère ...
Ce qui parait clair c'est que donkishot a raison de parler d'aérodynamisme car la sphère doit subir une force de pression de radiation bien moins importante que la surface du cercle . Ce qu'il a du calculer c'est le flux qui est égal , je crois dans les 2 cas (sphère et cercle ) , mais là il s'agit d'un rebond, ce n'est pas le flux ...
Bonne soirée .

[triall]

Bonjour à tous, et bien moi je continue, car ces calculs m'intéressent et ce serait bien de les appliquer à la Terre et au rayonnement solaire , pour évaluer la poussée qui devrait avoir tendance à éloigner la Terre du soleil (très faiblement sans doute).

Au dessus j'ai fait la démonstration que la quantité de mouvement du cercle allait vers le centre de celui ci , pour passer en 3d , c'est très simple , si, si .Il suffit de voir que ce rayonnement est celui que reçoit du soleil quelqu'un sur la Terre à une certaine latitude et longitude à l’équinoxe. (rayonnement perpendiculaire à l’axe nord-sud de la Terre)
On se met à sa place et on regarde en direction du soleil qui est à une certaine hauteur , il se réfléchit dans une mare bien lisse , ce qui donne , vue de côté le même dessin que plus haut. Dessin avec une démo plus simple encore .simple.jpg

Ainsi la quantité de mouvement est dirigée aussi à la verticale du point d'impact , vers le centre de la Terre . La norme du vecteur quantité de mouvement étant de 2m .cos téta , ou 2m sin.alpha alpha étant l'angle apparent que fait la particule avec l'horizontale .
Or, cet angle apparent que fait le soleil n'est autre que la hauteur (h terme astronomique) dont le sinus est égale comme chacun le sait à cos(latitude).cos (angle horaire) à l'équinoxe , ce qui est le cas ici .. sin(h)=cos(latitude).cos (angle horaire du soleil)
On a donc la norme du vecteur quantité de mouvement Mv2 de la sphère =2mvsin(h)=2mvcos(lat).cos(ang le horaire) soit en coordonnées sphériques comme alpha=pi/2-lat et angle horaire=téta (le même qu'en coordonnée sphérique)
2mv.sin(alpha).cos(téta) avec a point d'impact Oa=(r.cos(téta).sin(alpha); r.sin(téta).sin(alpha) ; r.sin(alpha) )
photon2.jpg
Résumé Mv2=Oa/r .2mvsin(alpha).cos(téta) maximum quand alpha= pi/2 et téta=0 .

Pour avoir l'accélération de la sphère il "suffit" de calculer le nombre de Mv2 par seconde dans l'axe de déplacement : l'axe des x , et de ne pas traiter les autres coordonnées qui s'annulent à droite et gauche et haut-bas de la sphère .. il reste donc
Quantité de mouvement au point d'impact a : Mv2=2mv .cos(téta)².sin(alpha)² i i étant vecteur unitaire de l'axe des x. Attention v négatif .
Sauf erreur !!!!
La suite je ne sais pas faire pour l'instant . Il faut faire ce qu'a dit LPFR , et par contre ça j'en suis... sûr , calculer le nombre de Mv2 par seconde(dirigés sur l'axe des x ) pour avoir directement l'accélération de la sphère . Attention aussi , cette accélération dans la réalité chute , car pour une bille , la vitesse d’impact v chute avec la vitesse de la sphère V2, (v-V2) pour un photon la fréquence diminue avec l’effet Doppler …
Bon réveillon .

[yootenhaiem]

Bonsoir,
Tout a fait, la terre est siege du rayonnement solaire. Et comme elle est supposée absorbante, on peut calculer la force qu'exerce les photons sur la terre, assimilée tout simplement, a un disque de rayon égal a celui de la terre, bombardé par des paquets de photons.
De ce qui est des calculs et de la modélisation que vous avez proposée Triall, je pense que c'est tout a fait juste. Le principe fondamental de la dynamique, nous donne, ou est la quantité de mouvement reçue par toute la sphère. Mais comme on a une certaine constance dans ce phénomène alors on pourrait faire cela: .
On n'aura donc besoin que du nombre de photon qui arrive sur la terre sur une periode et qu'on notera .
On peut donc integrer sur cette periode, et en remarquant que la force est constante: car le flux de photons l'est, on obtient: , ou est la quantité de mouvement reçue sur la période.
Le problème réside, en effet, dans le calcul de , ce qui nous invite a calculer la quantité de mouvement reçue par un point de la sphère, et d’intégrer ensuite sur toute la surface de la demi sphère(ou arrivent les photons), selon des paramètres bien choisis.
Sauf erreur, c'est ce que j'ai du faire dans mes calculs.

[triall]

Bonjour, j'ai revu vos équations et j'ai l'impression que votre x² est mon cos(téta)².sin(alpha)² !!! Je me rends compte que je me suis cassé la tête pour rien alors, x² est bien plus simple à intégrer ..
On a tous les 2 2 hv/c .il me semble que votre angle o est la hauteur (angle astronomique) dont je parle, par contre je ne vois pas ce qu'est a ! , ni i ni Ox Ux vous l'avez mis sur le dessin .... je ne sais pas de quoi à quoi vous intégrez , non plus !
Cos(2o) me parle aussi il y a un angle qui est double ...

Pouvez-vous détailler vos équations, cadeau un petit logiciel de géométrie très petit ...mais très intéressant , il ne s'installe pas on le copie simplement : http://www.1max2mov.net/GEOM.exe .
N'hésitez pas à me demander comment il fonctionne , je le connais par cœur .
Bon réveillon .

[yootenhaiem]

Bonsoir,
Alors le a= Rayon de la sphère.
Plaçons nous devant la sphère, on voit alors l'Axe (Ox) la traverser, et le vecteur (ux) directeur de cet axe.
Le mouvement des photons parallèlement a l'axe (Ox)et leur vecteur vitesse est dans le sens positif de (ux).
L'angle "i" est l'angle que fait OH, ou H est la projection du point M sur la sphère.avec l'axe(OY) perpendiculaire a (Ox) et dirigé verticalement.
Bon réveillon a vous aussi, et a toute la communauté FS.

[triall]

Bonjour, et bonne année à tous ...
Tout d'abord je dois corriger une bourde de ma part , en trouvant le nombre de hv/c par seconde on a la force que subit la sphère et non l'accélération (je pensais force et j'ai écris accélération) .

@ Donkishot :Vous avez calculé la quantité de mouvement reçue par la sphère pour 1 impact , vous trouvez selon l'axe U(x) 2hv/c(x²/a²) et moi 2hv/c.cos(theta)².sin(alpha)² (avec theta et alpha les angles du point d'impact M en sphérique) or a.cos(téta).sin(alpha) est la coordonnée x de OM donc on trouve la même chose .. La chapeau, car pour obtenir ce résultat je me suis tordu dans tous les sens !

Je n'avais pas vu ça, ce sera plus simple à intégrer mais je me demande de quoi à quoi(de 0 à a ?) Tandis que theta et alpha c'est de -pi/2 à pi/2.
Votre résultat ensuite en a3 n'est pas plausible , il me semble ,d'après ce que j'ai compris vous intégrez x² de 0 à a , vous avez du oublié de diviser par a² ensuite , il me semble , et i vous l'intégrez de -pi/2 à pi/2 ? je n 'ai pas compris ce que vous obtenez en écrivant P=4/3pia3 hv/c c'est quoi le P ?


Pour la surface réfléchissante du cercle de rayon a on trouve la force exercée F=(nombre de photon par sec par m²) .pi.a² . 2hc/v qui a bien la dimension d'une force :1/TL² .L².m .L/T=mL/T² . Pour une surface absorbante c'est 2 fois moins.

Il faudrait donc que le résultat de "notre "intégrale ait la dimension d'une surface... je veux bien intégrer mais je ne sais pas ce que ça donnerait ça n'a pas la dimension d'une surface peut-être faut-il multiplier ça par pi.a² surface apparente de contact !
Désolé de ne pouvoir vous aider plus , je ne calcule plus depuis longtemps, je pratique un peu ici en espérant que ça revienne et en essayant d'éviter les calculs "bestiaux" que je ne sais plus faire..

Bonne journée