[Thermique] Équation de la chaleur avec loi de Newton

[invited49614ed]

Bonjour,

Dans le cadre de mon TIPE je suis amené à étudier le cas suivant :

Dans un éprouvette ouverte à l'air libre, j'ai versé de l'eau bouillante et j'ai suivi l'évolution de la température de l'eau pendant 10 minutes.
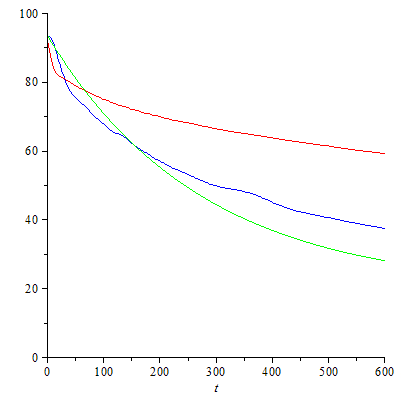
Puis rebelote, mais cette fois ci, l'éprouvette était plongée dans de l'aérogel de silice, qui est un excellent isolant. Le haut de l'éprouvette était quand même à l'air libre donc l'eau était en contact avec l'air. J'ai donc eu deux courbes, la première où la température de l'eau baissait fortement, la seconde, où la température baissait faiblement.

J'aimerais maintenant modéliser cette situation, et voir si une résolution numérique avec Maple aboutirait aux même courbes. Là où je bloque, c'est que je n'arrive pas à établir proprement l'équation de la chaleur en tenant compte des pertes dues au contact avec l'air. J'imagine qu'il faut considérer que la surface d'eau à l'air libre perd le transfert thermique δQ = hxSx(Ts - T0)xdt (qui est la loi de Newton, S la surface, h un coefficient, Ts la température de surface, T0 température de l'air constante).

Ensuite, dernière étape, il faudrait réussir à discrétiser l'équation de la chaleur, avec ce terme en plus. Je n'ai pas de mal pour discrétiser l'équation de la chaleur en elle même, mais on verra bien ce que ça donne avec ce fameux terme en plus!

Merci pour toutes vos réponses.
-----

[inviteb901c22f]

Bonjour,
Dans cet exemple j’écrirais que le refroidissement du volume v d’eau de masse spécifique C est égal
Aux pertes thermiques à travers la résistance thermique Rth de l’éprouvette.
J’obtiens une loi de décroissance exponentielle :

Ou Te=température extérieure Tfo=température initiale de l’eau ro=masse volumique
C=chaleur spécifique V=volume de l’eau Rth=résistance thermique de l’éprouvette
En prenant en première approximation
Ou S est la surface de l’éprouvette et h le coefficient de convection
On obtient :


Cordialement

[invited49614ed]

Oui vous avez raison, c'est beaucoup plus simple de faire ainsi. Je pense que je vais garder votre approche!

Cependant, je ne vois pas comment trouver l'expression de la quantité de chaleur perdue dans le cas où l'éprouvette est entourée d'aérogel de silice. Ni quel pourrait être la résistance thermique équivalente!

[inviteb901c22f]

Bonjour,
Dans le cas ou l’éprouvette est entourée de gel de silice,il faut faire intervenir la conductivité thermique du gel.Je ne connais pas la géométrie exacte du réservoir mais en supposant un réservoir cylindrique de hauteur L de rayon externe re et de rayon interne ri(ri égal aussi au rayon externe de l’éprouvette ?) on peut écrire :

Ou hi=coefficient de convection interne(eau éprouvette)
Si=surface (interne)de l’éprouvette
k=conductivité du gel de silice
he=coefficient de convection externe(réservoir –air)
Se=surface du réservoir
J’ai négligé la résistance thermique due à la conductivité de l’éprouvette(à vérifier)
cordialement

[A voir en vidéo sur Futura]

[invited49614ed]

Oui c'est ça, l'éprouvette était entourée d'aérogel dans un récipient cylindrique. De plus l'éprouvette était très mince et de capacité thermique massique négligeable devant celle de l'eau. À mon avis, avec vos notations, comme l'aérogel est un très bon isolant (k≈0.017 W.m^-1.K^-1) on peut de plus supposer que la température de l'aérogel en re vaut Te. Il n'y a donc pas de flux de chaleur par convection. Ce que je n'arrive pas à faire cette fois ci c'est établir la résistance thermique équivalente pour l'aérogel. En fait rien que l'application du premier principe à l'eau pose problème...

Je ne vois pas ce que représente hi, l'eau étant immobile, pourquoi y aurait-il un terme de convection interne?

[inviteb901c22f]

Bonjour,
La résistance thermique du gel de silice est le terme :
hi (qui traduit l'échange thermique entre l'eau et la paroi interne du tube) est probablement très grand de sorte que l’on peut négliger le terme
Je n’ai pas les dimensions du pb mais en prenant par exemple :ri=1 cm,re=5 cm,L=20 cm,k=0,017
On a : :
Et si on prend he=12 Wm-2K-1
Le terme prépondérant à prendre en compte est donc bien le second terme

cordialement

[invited49614ed]

Bonjour,

D'accord, je comprend ce que vous faites. Et ensuite, pour obtenir l'expression de T(t), vous écrivez le premier principe :
dU = rho*c*V*dT = 1/Rth * (T0-T(t))

Ce qui donne :
T(t) = T0 + (Ti-T0)*exp(-t/(Rho*C*V*Rth))

Le problème c'est que ceci ne permet pas d'expliquer la courbe que j'ai obtenu expérimentalement :

XXXXXXXXXXXXXXXXXXXXX

en rouge, celle obtenue avec l'aérogel.

Il y a un changement de pente vers t=10s. En fait, qualitativement on peut expliquer cela par le fait que pendant les 10 premières secondes, l'aérogel se réchauffe puis les échanges thermiques avec l'aérogel sont négligeables et seules se font ceux avec l'air.

Pour t>10s j'ai modélisé la courbe par :
T(t) = T0+CTE*exp(-h*S*t/(rho*C*V)) avec la méthode précédente

Par contre pour t<10s, une modélisation correcte est obtenue avec :
T(t) = Ti*exp(-t/b)
Mais je ne vois pas comment obtenir une équation de ce type.
Par homogénéité, on peut exprimer b par :
b= rho*C*V/(K*L)
à une constante multiplicative près.

Auriez vous des pistes?

[invited49614ed]

Enfait je suis débile, pour t<10s c'est l'expression de la résistance thermique de l'aérogel... Je vais quand même vérifier si ça concorde avec les données!

[inviteb901c22f]

bonjour,
oui en présence de l'aerogel la déperdition se fait par conduction à travers l'aérogel et c'est sa résistance thermique qui entre en jeu.
cordialement

[obi76]

Bonjour,

l'hébergement d'images sur serveurs externes est interdit. Merci de les insérer en pièces jointes.

Pour la modération,

[invited49614ed]

Voilà les courbes obtenues pour les intéressés