Effet larsen

[jeuxjeux]

Désolé de faire un nouveau message, mais on a que 5 minutes pour changer un message, je voudrai rajouter :

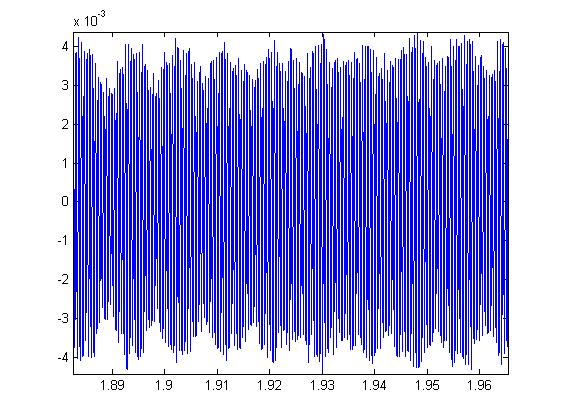
il est tout à fait possible finalement que l'on aie une superposition de deux fréquences, une basse et une élevée. Elles semblent même avoir la même amplitude, c'est ce que montre le graphique en tout cas. Ainsi, l'effet Larsen se produirait (du moins sans saturation) avec une apparition de deux fréquences, l'une à basse fréquence, l'autre à haute fréquence. Il faudrait vérifier que la basse fréquence soit celle du temps de propagation entre le micro et le baffle. Mais vu que les fréquences affichées ne sont à nouveau plus bonnes. Cette basse fréquence apparaît, que l'on aie ou non du bruit. Ce n'est donc pas un hasard du à un choix d'une entrée spécifique.

Voici une image afin de mieux comprendre ce qu'il se passe :

On voit la superposition d'une onde basse et haute fréquence, c'était toujours le cas depuis le début, mais je n'y faisait pas attention, voyant uniquement la haute fréquence et considérant la basse fréquence comme allant disparaître dans le temps.

A+

J'attends vos remarques et commentaires !
-----

[phuphus]

Bonsoir jeuxjeux,

je vois que ça avance bien !

J'attends vos remarques et commentaires !

Ça tombe bien, j'en ai quelques-unes et quelques-uns

1) j'ai fait la correction au niveau des fréquences (comme tu l'a fait remarqué, les fréquences affichées ne sont pas les bonnes, c'est résolu)

OK ! Je ne vérifie pas, je te donnerai juste quelques éléments plus tard dans le message pour vérifier toi-même.

3) je n'ai jamais entendu parlé de waterfall ou de sonogramme, je vais y jeter un coup d'oeil.

Sur un sonagramme, on représente l'évolution des fréquences sur une image avec :
- sur un axe, le temps
- sur l'autre axe, la fréquence
- l'amplitude en code couleur

Tu en as donc fait un sans le savoir (c'est ta "Projection à 2 dimensions où les couleurs représentent l'intensité").

les fréquences affichées dépendent linéairement du nombre d'échantillon (il doit y avoir une division par le nombre d'échantillon qu'il manque quelque part)

Une FFT à court terme sur un signal discret n'est rien d'autre qu'une série de Fourier. La première fréquence renvoyée par la FFT est la composante continue, ensuite il s'agit tout simplement de l'harmonique 1 sur la période d'analyse, puis les multiples.

Donc si tu as une fréquence d'échantillonnage de 100 kHz et une FFT de 1000 points, ta période d'analyse est de 0.01s, et la FFT te renvoie toutes les fréquences multiples de 100Hz. Avec une période de 0.1s, la base est 10Hz ; avec une période de 0.5s, la base est 2Hz ; etc.

zoom sur une petite partie, on voit la périodicité dans le temps, ce qui semble quelque peu étonnant (complètement faux?), temps(720-810)/fréquences(985-1020)

Les outils d'analyse temps-fréquence ne sont pas facile à apprivoiser, notamment dès qu'il y a de la modulation d'amplitude. Une période d'analyse trop courte et la raie est interrompue, une période d'analyse plus longue et la modulation d'amplitude apparaît comme des raies latérales de la fréquence modulée. De plus, avec les effets de bord, si le nombre de périodes de la fréquence considérée est faible sur la période d'analyse, on a une périodicité des effets de bord qui fait croire à de la modulation. Je n'en dis pas plus, ça nous emmènerait trop loin.

Projection à 2 dimensions où les couleurs représentent l'intensité

Tu n'aurais pas tracé par hasard tous les points de la FFT plutôt que la première moitié ? Je pense que si... Tu viens donc d'illustrer la symétrie du spectre par rapport à la fréquence de Nyquist, et non une réponse du Larsen sur deux fréquences.

Voici une image afin de mieux comprendre ce qu'il se passe :
Pièce jointe 195600
On voit la superposition d'une onde basse et haute fréquence, c'était toujours le cas depuis le début, mais je n'y faisait pas attention, voyant uniquement la haute fréquence et considérant la basse fréquence comme allant disparaître dans le temps.

Véritable modulation sur la signal ou bien simple modulation "graphique" due à un effet de moiré ?

Je te renvoie un code intégrant la saturation, et comparant 4 cas :
- excitation Dirac sans saturation
- excitation Dirac avec saturation
- excitation bruit blanc + Dirac sans saturation
- excitation bruit blanc + Dirac sans saturation

Je me suis placé exprès avec des paramètres limites, qui font que :
- le système accroche à la fois sur 580Hz et son harmonique 2 avant la saturation, et c'est le 580 Hz qui gagne après saturation
- le système accroche préférentiellement sur 1160Hz (harmonique 2) en bruit blanc, mais le 580 Hz émerge et le dépasse presque de temps à autres, j'ai même vu une simulation où le système finit par bifurquer sur 580 Hz (image en pièce jointe).

Sur l'image en pièce jointe :
- à gauche : sans saturation
- à droite : avec saturation

Sur le système sans saturation, c'est le 1160 Hz qui gagne.
Sur le système avec saturation, le 1160 Hz fait la course en tête pendant quelques centièmes de seconde, puis le système bifurque sur 580 Hz.

En changeant un chouilla les paramètres (augmentation du facteur de qualité et modif ad-hoc de la distance ampli / micro, le facteur de qualité faisant bouger la fréquence de résonance), on peut faire accrocher le système en excitation Dirac sur l'harmonique 2 tout en conservant le fondamental à une amplitude moindre (on a donc bien deux fréquences !). On a du coup l'impression d'un sous-harmonique, et cela ressemble assez aux résultats de ton tout premier code.

Remarques : le code n'est pas aussi propre que ce que j'ai mis précédemment, je le finaliserai dans les jours qui viennent. Et j'ai un problème d'échelle de temps sur les sonags sans saturation, à voir.

Script principal :

% Simulation d'un effet Larsen via un filtre résursif
% On a une chaine micro + préampli micro + ampli + HP + propagation
% Le microphone recapte l'onde sonore, et on est repartis pour un tour
% La FTBO s'entend comme le rapport Pression / Pression au microphone

clear all ;
clc ;

% Paramètres
  Dist = 0.56 ;  % Distance micro / ampli [m]
  Q    = 0.8  ;  % Facteur de surtension à la résonance

% Définition des données utiles
  c          = 340                           ;  % Vitesse des ondes sonores   [m/s]
  Fech       = 50000                         ;  % Fréquence d'échantillonnage [Hz]
  pas        = 1/Fech                        ;  % Pas de temps                [s]
  Nyquist    = round(Fech/2)                 ;  % Fréquence de Nyquist        [Hz]
  Nfft       = Fech                          ;  % => DeltaF = 1 Hz
  Duree      = 0.1                           ;  % Durée de la simulation      [s]
  t          = [0:pas:Duree-pas]             ;  % Vecteur temps               [s]
  f          = [0:Fech/(Duree*Nfft):Nyquist] ;  % Vecteurs fréquences         [Hz]
  w          = 2*pi*f                        ;  % Vecteurs pulsations         [rad/s]
  % f_tot   = [0:Fech/(Duree*Nfft):Fech-Fech/(Duree*Nfft)]    ;
  % w_tot   = 2*pi*f_tot ;  
  Nfft_sonag = 16384 ;
  Nrecouvr   = 500 ;
  Fenetre    = Hanning(512) ;
  
% Données physiques
  Gain_micro       =   0.01     ;  % Gain du microphone     [V/Pa]
  Gain_preamp      =  18.00     ;  % Gain du préampli micro [V/V]
  Gain_ampli       =  20.00     ;  % Gain de l'ampli        [V/V]
  Gain_HP_1m       =   0.10     ;  % Gain du haut-parleur   [Pa/V] à 1m
  Gain_propagation = (1/Dist)^2 ;  % Gain du à la distance  [Pa/Pa]
  
% Hypothèse : la fonction de transfert globale est assimilable à un système
% masse-ressort avec Q défini dans les paramètres
% Critiques
% 1 - On passe toutes les BF, alors que l'on devrait avoir une coupure
% d'ordre 2 (enceinte close) ou d'ordre 4 (bass-reflex).
% 2 - Une seule résonance de bout de bande, alors qu'un HP d'ampli guitare en a plusieurs
% => Quel ordre pour un HP en baffle ouvert comme dans la plupart des amplis guitarre ??
  % Définition des paramètres du système masse-ressort
    k       = 150e6       ;  % Raideur du ressort [N/m]
    m       = 1           ;  % Masse              [kg]
    w0      = sqrt(k/m)   ;  % Pulsation propre   [rad/s]
    f0      = w0 /(2*pi)  ;  % Fréquence propre   [Hz]
    b       = sqrt(k*m)/Q ;  % Amortissement      [kg/s]
    
  % Construction de la réponse impulsionnelle du système masse-ressort
    FT      = 1./(-w.^2*m + j*b*w + k)     ;  % Fonction de transfert
    FT      = k * FT                       ;  % Fonction de transfert normalisée
    Taille  = size(FT,2)                   ;
    FT_inv  = [FT conj(FT(Taille-1:-1:2))] ;  % Fonction de transfert inversible par FFT-1
    RI_ms   = real(ifft(FT_inv))           ;  % Réponse impulsionnelle
    
  % Construction de la RI globale
    Taille = max(find(RI_ms(:)>max(RI_ms)/1000)) + 1  ;
    RI_ms  = RI_ms(1:Taille) ;
    Taille = Taille + round(Fech*Dist/c) ;
    RI_glob = zeros(1,Taille) ;
    % Détail de chacune des contributions
      RI_micro            = RI_glob            ;
      RI_preamp           = RI_glob            ;
      RI_ampli            = RI_glob            ;
      RI_HP               = RI_glob            ;
      RI_propagation      = RI_glob            ;
      RI_micro(1)         = Gain_micro         ;
      RI_preamp(1)        = Gain_preamp        ;
      RI_ampli(1)         = Gain_ampli         ;
      RI_HP(1)            = Gain_HP_1m         ;
      Ind                 = round(Fech*Dist/c) ;
      RI_propagation(Ind) = Gain_propagation   ;
    % RI globale
      RI_glob(1) = 1                                ;
      RI_glob    = filter(RI_micro      ,1,RI_glob) ;
      RI_glob    = filter(RI_preamp     ,1,RI_glob) ;
      RI_glob    = filter(RI_ampli      ,1,RI_glob) ;
      RI_glob    = filter(RI_HP         ,1,RI_glob) ;
      RI_glob    = filter(RI_propagation,1,RI_glob) ;
      RI_glob    = filter(RI_ms         ,1,RI_glob) ;
      
  % Utilisation d'un filtre récursif
  % La partie directe est égale à la RI globale
  % La partie récursive est égale à -RI_glob, avec un premier coefficient forcé à 1
    RI_dir    =  RI_glob ;
    RI_rec    = -RI_glob ;
    RI_rec(1) =  1       ;
    
  % Construction d'un signal d'excitation
  % Essai 1 : Pseudo-Dirac
    Taille         = size(t,2)                    ;
    Signal         = zeros(1,Taille)              ;
    Signal(1)      = 1                            ;
    Resultat_Dirac = filter(RI_dir,RI_rec,Signal) ;
    
    
    % Equation de récurrence gérée à la main + saturation
    Taille_signal         = size(Signal ,2)        ;
    Taille_filtre         = size(RI_glob,2)        ;
    Resultat_Dirac_manuel = zeros(1,Taille_signal) ;
    for i = 1:Taille
      Taille_conv = min(Taille_filtre,i) ;
      Resultat_Dirac_manuel(i) = (sum(RI_dir(1:Taille_conv).*Signal(i:-1:i-Taille_conv+1)) - sum(RI_rec(2:Taille_conv).*Resultat_Dirac_manuel(i-1:-1:i-Taille_conv+1))) / RI_rec(1) ;
      Resultat_Dirac_manuel(i) =  saturation(Resultat_Dirac_manuel(i),1)                                                                                                            ;
    end
  
    % plot(t,Resultat_Dirac_manuel,'r') ;
    % hold off ;
    
    % Construction des sonagrammes
    [Amp        Freq Temps] = specgram(Resultat_Dirac       ,Nfft_sonag,Fech,Fenetre,Nrecouvr) ;
    [Amp_manuel Freq Temps] = specgram(Resultat_Dirac_manuel,Nfft_sonag,Fech,Fenetre,Nrecouvr) ;
    
    % Tracés
      figure(1) ;
      subplot(2,2,1) ;
      plot(t,Resultat_Dirac) ;
      subplot(2,2,2) ;
      plot(t,Resultat_Dirac_manuel) ;
      subplot(2,2,3) ;
      imagesc(Temps, Freq(1:2049,:), (abs(Amp       (1:2049,1)))) ;
      axis xy ;
      subplot(2,2,4) ;
      imagesc(Temps, Freq(1:2049,:), (abs(Amp_manuel(1:2049,:)))) ;
      axis xy ;
    
  % Essai 2 : Bruit blanc
    Taille         = size(t,2)                    ;
    Signal         = rand(1,Taille) - 0.5              ;
    Signal(1)      = 1                            ;
    Resultat_Dirac = filter(RI_dir,RI_rec,Signal) ;
    
    % Equation de récurrence gérée à la main + saturation
    Taille_signal         = size(Signal ,2) ;
    Taille_filtre         = size(RI_glob,2) ;
    Resultat_Dirac_manuel = zeros(1,Taille_signal) ;
    for i = 1:Taille
      Taille_conv = min(Taille_filtre,i) ;
      Resultat_Dirac_manuel(i) = (sum(RI_dir(1:Taille_conv).*Signal(i:-1:i-Taille_conv+1)) - sum(RI_rec(2:Taille_conv).*Resultat_Dirac_manuel(i-1:-1:i-Taille_conv+1))) / RI_rec(1) ;
      Resultat_Dirac_manuel(i) = saturation(Resultat_Dirac_manuel(i),1) ;
    end
    
    % Construction des sonagrammes
    [Amp        Freq Temps] = specgram(Resultat_Dirac       ,Nfft_sonag,Fech,Fenetre,Nrecouvr) ;
    [Amp_manuel Freq Temps] = specgram(Resultat_Dirac_manuel,Nfft_sonag,Fech,Fenetre,Nrecouvr) ;
    
    % Tracés
      figure(2) ;
      subplot(2,2,1) ;
      plot(t,Resultat_Dirac) ;
      subplot(2,2,2) ;
      plot(t,Resultat_Dirac_manuel) ;
      subplot(2,2,3) ;
      imagesc(Temps, Freq(1:2049,:), (abs(Amp       (1:2049,1)))) ;
      axis xy ;
      subplot(2,2,4) ;
      imagesc(Temps, Freq(1:2049,:), (abs(Amp_manuel(1:2049,:)))) ;
      axis xy ;

Script secondaire "saturation.m" :

% Fonction de gestion de saturation
% Pour l'instant : saturation type transistor
% Possibilité de faire une simulation (grossière) d'ampli à lampes
% en adoucissant le coude

function y = saturation(x,sat)
  y = min(abs(x),sat)*sign(x) ;

[jeuxjeux]

Merci beaucoup Phuphus,

Tout d'abord rendons à César ce qui est à César, c'est parce que tu m'as parlé de sonogramme et de waterfall que j'ai fait l'analyse que tu as vue.

Je me disais bien que l'analyse fréquentiel était largement dépendante de ce sur la période sur laquelle on fait la FFT (nombre de point), mais je n'ai pas compris cette phrase : "une période d'analyse plus longue et la modulation d'amplitude apparaît comme des raies latérales de la fréquence modulée", cela veut-il dire que l'on obtient une fréquence qui reste à la même amplitude, mais aussi d'autres fréquences qui apparaissent? (j'avais d'ailleurs fait plusieurs tests selon la longueur de la DFT mais n'ai jamais réussi à me débarrasser totalement du côté sinusoïdale de l'amplitude de certaines fréquences, même avec un très grand nombre de points)

A propos des effets de bords, je veux bien aller un peu plus loin. Mon but est de comprendre un maximum de choses et de maîtriser des outils d'analyse fréquentiel, car j'en aurai de toute façon besoin par la suite, en plus d'être intéressant en soi. La raison pour laquelle je ne comprend pas que cela change, c'est que le résultat devrait donner les même fréquences, avec la même amplitude, mais avec une phase différente, or la phase disparaît vu que je prend le module du résultat de la FFT. Qu'en est-il alors?

Lorsque vous dites : "Tu viens donc d'illustrer la symétrie du spectre par rapport à la fréquence de Nyquist", est-ce simplement un repliement spectral? Le fait que vu l'echantillonage, on ne puisse distinguer des fréquences séparées d'une certaine distance? Je me disais aussi que ce n'était pas physique, car j'avais par après pu résoudre une fois encore un problème d'échelle de fréquences et j'avais vu que l'une des fréquences était physique, mais que l'autre était bien trop grande.

Donc, maintenant, on a la réponse : il peut y avoir plusieurs fréquences en même temps. Par contre, le sonogramme ne veut strictement rien dire, vu que il ne varie absolument pas selon le temps. Ce qu'il me semble étonnant, c'est que l'on ait une fréquence nulle qui apparaît dans le spectre, cela veut dire que le baffle passe plus de temps à l'une de ses extrémités qu'à l'autre extrémité, et que donc, le fait d'être à une extrémité est un état stable?

Par contre, ça m'embête toujours, à chaque fois que je fais quelque chose à la main, je vois par après, que vous utilisez une fonction spécifique. Je pense que je devrais vraiment passer plus de temps dans l'aide Matlab, c'est frustrant de se dire que l'on a pas besoin de le faire et que tellement de choses on déjà été codées pour nous.

Au fait, je n'ai pas pu avoir accès à l'image que tu as mise, car il faut attendre l'approbation d'un modérateur, si par contre, tu le mets dans le message, on peut y avoir accès tout de suite. Ah voilà, je les vois, très belles en effet !

Merci pour tout, ça devient franchement beau, je vais essayer de comprendre un peu plus en détail le code envoyé, puis, on verra,...
A+

[phuphus]

Bonsoir,

Je me disais bien que l'analyse fréquentiel était largement dépendante de ce sur la période sur laquelle on fait la FFT (nombre de point), mais je n'ai pas compris cette phrase : "une période d'analyse plus longue et la modulation d'amplitude apparaît comme des raies latérales de la fréquence modulée", cela veut-il dire que l'on obtient une fréquence qui reste à la même amplitude, mais aussi d'autres fréquences qui apparaissent? (j'avais d'ailleurs fait plusieurs tests selon la longueur de la DFT mais n'ai jamais réussi à me débarrasser totalement du côté sinusoïdale de l'amplitude de certaines fréquences, même avec un très grand nombre de points)

Oui, si l'analyse d'un sinus modulé en amplitude se fait sur un nombre suffisant de périodes de modulation, alors les fréquences contenues dans l'enveloppe apparaissent comme des raies latérales.

A propos des effets de bords, je veux bien aller un peu plus loin. Mon but est de comprendre un maximum de choses et de maîtriser des outils d'analyse fréquentiel, car j'en aurai de toute façon besoin par la suite, en plus d'être intéressant en soi. La raison pour laquelle je ne comprend pas que cela change, c'est que le résultat devrait donner les même fréquences, avec la même amplitude, mais avec une phase différente, or la phase disparaît vu que je prend le module du résultat de la FFT. Qu'en est-il alors?

C'est vrai sur un signal stationnaire, mais ici l'amplitude évolue. Par contre, je pense que tu as raison, cette évolution n'est pas suffisamment brusque pour justifier ce que l'on voit. Je te propose donc autre chose, à la ligne suivante :

Y(i+1,:) = abs(real(fft(Resultat_Dirac(di st*i+1:dist*i+L),NFFT)/L));

enlève le "real", et tout devrait bien se passer

Lorsque vous dites : "Tu viens donc d'illustrer la symétrie du spectre par rapport à la fréquence de Nyquist", est-ce simplement un repliement spectral? Le fait que vu l'echantillonage, on ne puisse distinguer des fréquences séparées d'une certaine distance? Je me disais aussi que ce n'était pas physique, car j'avais par après pu résoudre une fois encore un problème d'échelle de fréquences et j'avais vu que l'une des fréquences était physique, mais que l'autre était bien trop grande.

On ne peut pas vraiment parler de repliement ici, vu que l'on n'a aucune fréquence plus grande que la fréquence de Nyquist. Le spectre d'un signal réel est symétrique, le spectre d'un signal discret est périodique, et pour un signal échantillonné seules les fréquences comprise entre 0 et la fréquence de Nyquist ("FNyquist") ont du sens. Par construction, une FFT respecte cette symétrie, avec la moitié de l'"énergie" du signal contenue dans les fréquences positives et l'autre moitié dans les fréquences négatives. L'habitude avec la FFT est de re-balancer les fréquences négatives entre FNyquist et Fech, c'est pour cela que sur tes images la symétrie du spectre est affichée par rapport à FNyquist. Quant à la fréquence trop grande, tu sais donc maintenant qu'elle est égale à Fech-F, avec F fréquence du Larsen, et que la moitié de l'énergie de la fréquence du Larsen apparaît à F, et l'autre moitié à Fech-F.

La discrimination fréquentielle dépend de l'analyse spectrale, mais pas de la fréquence d'échantillonnage. Regarde du côté de :
- zero padding (augmentation artificielle de la longueur de la période d'analyse, j'en fais intensivement dans le sonag de mon code)
- zoom fft (plus délicat, utilisation des propriétés de la modulation d'amplitude)

Donc, maintenant, on a la réponse : il peut y avoir plusieurs fréquences en même temps. Par contre, le sonogramme ne veut strictement rien dire, vu que il ne varie absolument pas selon le temps. Ce qu'il me semble étonnant, c'est que l'on ait une fréquence nulle qui apparaît dans le spectre, cela veut dire que le baffle passe plus de temps à l'une de ses extrémités qu'à l'autre extrémité, et que donc, le fait d'être à une extrémité est un état stable?

Avec la suppression du "real" gênant, tu verras qu'il évolue. Quant au sonag sur Larsen sans saturation de ma dernière image jointe, il est faux puisque j'ai pris par erreur le tout premier spectre du sonag à tout instant (d'où mon problème d'échelle de temps). Tu peux le voir dans mon code :

imagesc(Temps, Freq(1:2049,:), (abs(Amp (1:2049,1)))) ;

à corriger par :

imagesc(Temps, Freq(1:2049,:), (abs(Amp (1:2049,:)))) ;

Code corrigé à venir !

La fréquence nulle est la composante continue, et comme je le souligne dans mon code :

% Hypothèse : la fonction de transfert globale est assimilable à un système
% masse-ressort avec Q = 3
% Critiques
% 1 - On passe toutes les BF, alors que l'on devrait avoir une coupure
% d'ordre 2 (enceinte close) ou d'ordre 4 (bass-reflex).

J'ai donc volontairement adopté une fonction de transfert qui passe le continu (modification de la pression atmosphérique moyenne), si tu veux on peux faire quelque chose de plus réaliste. Genre une coupure à l'ordre 4 ou 6 vers 150 - 200 Hz, ça doit être assez réaliste pour un 30 cm dans un ampli guitare en baffle ouvert (à vérifier...).

Pour l'anecdote, seul un haut-parleur étanche en enceinte close dans une pièce parfaitement étanche passe le continu (mise en compression / dépression de la pièce), mais certainement pas avec une réponse en fréquence plate jusqu'au continu. Pour faire court : un HP est un système masse-ressort, en contrôle de masse au dessus de la fréquence propre et en contrôle de raideur en dessous. A peu de choses près, la pression acoustique générée est proportionnelle à l'accélération de la membrane (donc ça chute forcément à l'ordre 2 en dessous de la fréquence propre), alors que pour le continu elle sera dépendante du volume balayé suite à la variation de la position de repos de la membrane comparé au volume de la pièce.

Par contre, ça m'embête toujours, à chaque fois que je fais quelque chose à la main, je vois par après, que vous utilisez une fonction spécifique. Je pense que je devrais vraiment passer plus de temps dans l'aide Matlab, c'est frustrant de se dire que l'on a pas besoin de le faire et que tellement de choses on déjà été codées pour nous.

Frustrant mais très pédagogique... J'en suis aussi là sur beaucoup de fonctions Matlab.

Merci pour tout, ça devient franchement beau, je vais essayer de comprendre un peu plus en détail le code envoyé, puis, on verra,...

Je mets quelques corrections et ajouts, notamment un tracé du gain du filtre IIR, permettant de voir quelles fréquences sont au dessus de 0dB, c'est à dire quelles fréquences vont "Larséner". Amuse-toi bien !

A venir : réels sonagrammes d'amplitude, à l'heure actuelle je n'ai pas vérifié si la commande specgram renvoie des FFT brutes ou si elle divise par la longueur d'analyse.

[phuphus]

Le code, qui ne passait pas dans le message précédent (> 15 000 caractères) :

% Simulation d'un effet Larsen via un filtre résursif
% On a une chaine micro + préampli micro + ampli + HP + propagation
% Le microphone recapte l'onde sonore, et on est repartis pour un tour
% La FTBO s'entend comme le rapport Pression / Pression au microphone

clear all ;
clc ;

% Paramètres
  Dist = 0.56 ;  % Distance micro / ampli [m]
  Q    = 0.8  ;  % Facteur de surtension à la résonance

% Définition des données utiles
  c          = 340                           ;  % Vitesse des ondes sonores   [m/s]
  Fech       = 50000                         ;  % Fréquence d'échantillonnage [Hz]
  pas        = 1/Fech                        ;  % Pas de temps                [s]
  Nyquist    = round(Fech/2)                 ;  % Fréquence de Nyquist        [Hz]
  Nfft       = Fech                          ;  % => DeltaF = 1 Hz
  Duree      = 0.1                           ;  % Durée de la simulation      [s]
  t          = [0:pas:Duree-pas]             ;  % Vecteur temps               [s]
  f          = [0:Fech/(Duree*Nfft):Nyquist] ;  % Vecteurs fréquences         [Hz]
  w          = 2*pi*f                        ;  % Vecteurs pulsations         [rad/s]
  % f_tot   = [0:Fech/(Duree*Nfft):Fech-Fech/(Duree*Nfft)]    ;
  % w_tot   = 2*pi*f_tot ;  
  Nfft_sonag = 16384 ;
  Nrecouvr   = 500 ;
  Fenetre    = Hanning(512) ;
  
% Données physiques
  Gain_micro       =   0.01     ;  % Gain du microphone     [V/Pa]
  Gain_preamp      =  18.00     ;  % Gain du préampli micro [V/V]
  Gain_ampli       =  20.00     ;  % Gain de l'ampli        [V/V]
  Gain_HP_1m       =   0.10     ;  % Gain du haut-parleur   [Pa/V] à 1m
  Gain_propagation = (1/Dist)^2 ;  % Gain du à la distance  [Pa/Pa]
  
% Hypothèse : la fonction de transfert globale est assimilable à un système
% masse-ressort avec Q défini dans les paramètres
% Critiques
% 1 - On passe toutes les BF, alors que l'on devrait avoir une coupure
% d'ordre 2 (enceinte close) ou d'ordre 4 (bass-reflex).
% 2 - Une seule résonance de bout de bande, alors qu'un HP d'ampli guitare en a plusieurs
% => Quel ordre pour un HP en baffle ouvert comme dans la plupart des amplis guitarre ??
  % Définition des paramètres du système masse-ressort
    k       = 150e6       ;  % Raideur du ressort [N/m]
    m       = 1           ;  % Masse              [kg]
    w0      = sqrt(k/m)   ;  % Pulsation propre   [rad/s]
    f0      = w0 /(2*pi)  ;  % Fréquence propre   [Hz]
    b       = sqrt(k*m)/Q ;  % Amortissement      [kg/s]
    
  % Construction de la réponse impulsionnelle du système masse-ressort
    FT      = 1./(-w.^2*m + j*b*w + k)     ;  % Fonction de transfert
    FT      = k * FT                       ;  % Fonction de transfert normalisée
    Taille  = size(FT,2)                   ;
    FT_inv  = [FT conj(FT(Taille-1:-1:2))] ;  % Fonction de transfert inversible par FFT-1
    RI_ms   = real(ifft(FT_inv))           ;  % Réponse impulsionnelle
    
  % Construction de la RI globale
    Taille = max(find(RI_ms(:)>max(RI_ms)/1000)) + 1  ;
    RI_ms  = RI_ms(1:Taille) ;
    Taille = Taille + round(Fech*Dist/c) ;
    RI_glob = zeros(1,Taille) ;
    % Détail de chacune des contributions
      RI_micro            = RI_glob            ;
      RI_preamp           = RI_glob            ;
      RI_ampli            = RI_glob            ;
      RI_HP               = RI_glob            ;
      RI_propagation      = RI_glob            ;
      RI_micro(1)         = Gain_micro         ;
      RI_preamp(1)        = Gain_preamp        ;
      RI_ampli(1)         = Gain_ampli         ;
      RI_HP(1)            = Gain_HP_1m         ;
      Ind                 = round(Fech*Dist/c) ;
      RI_propagation(Ind) = Gain_propagation   ;
    % RI globale
      RI_glob(1) = 1                                ;
      RI_glob    = filter(RI_micro      ,1,RI_glob) ;
      RI_glob    = filter(RI_preamp     ,1,RI_glob) ;
      RI_glob    = filter(RI_ampli      ,1,RI_glob) ;
      RI_glob    = filter(RI_HP         ,1,RI_glob) ;
      RI_glob    = filter(RI_propagation,1,RI_glob) ;
      RI_glob    = filter(RI_ms         ,1,RI_glob) ;
      
  % Utilisation d'un filtre récursif
  % La partie directe est égale à la RI globale
  % La partie récursive est égale à -RI_glob, avec un premier coefficient forcé à 1
    RI_dir    =  RI_glob ;
    RI_rec    = -RI_glob ;
    RI_rec(1) =  1       ;
    
  % Tracé de la fonction de transfert du filtre
    [H,F] = freqz(RI_dir,RI_rec,Fech,Fech) ;
    figure(1)
    semilogx(F,20*log10(abs(H))) ;
    axis([0 Fech/2 -20 40]) ;
    xlabel('Fréquence (Hz)') ;
    ylabel('Gain (dB)') ;
    Title(['Gain du filtre IIR modélisant le Larsen. Distance ampli / micro : ' sprintf('%.2f',Dist) 'm'])  
    
  % Construction d'un signal d'excitation
  % Essai 1 : Pseudo-Dirac
    Taille         = size(t,2)                    ;
    Signal         = zeros(1,Taille)              ;
    Signal(1)      = 1                            ;
    Resultat_Dirac = filter(RI_dir,RI_rec,Signal) ;
    
    
    % Equation de récurrence gérée à la main + saturation
    Taille_signal         = size(Signal ,2)        ;
    Taille_filtre         = size(RI_glob,2)        ;
    Resultat_Dirac_manuel = zeros(1,Taille_signal) ;
    for i = 1:Taille
      Taille_conv              = min(Taille_filtre,i)                                                                                                                               ;
      Resultat_Dirac_manuel(i) = (sum(RI_dir(1:Taille_conv).*Signal(i:-1:i-Taille_conv+1)) - sum(RI_rec(2:Taille_conv).*Resultat_Dirac_manuel(i-1:-1:i-Taille_conv+1))) / RI_rec(1) ;
      Resultat_Dirac_manuel(i) =  saturation(Resultat_Dirac_manuel(i),1)                                                                                                            ;
    end
    
    % Construction des sonagrammes
    [Amp        Freq Temps] = specgram(Resultat_Dirac       ,Nfft_sonag,Fech,Fenetre,Nrecouvr) ;
    [Amp_manuel Freq Temps] = specgram(Resultat_Dirac_manuel,Nfft_sonag,Fech,Fenetre,Nrecouvr) ;
    
    % Tracés
      figure(10) ;
      subplot(2,2,1) ;
      plot(t,Resultat_Dirac) ;
      subplot(2,2,2) ;
      plot(t,Resultat_Dirac_manuel) ;
      subplot(2,2,3) ;
      imagesc(Temps, Freq(1:2049,:), (abs(Amp       (1:2049,:)))) ;
      axis xy ;
      subplot(2,2,4) ;
      imagesc(Temps, Freq(1:2049,:), (abs(Amp_manuel(1:2049,:)))) ;
      axis xy ;
    
  % Essai 2 : Bruit blanc
    Taille         = size(t,2)                    ;
    Signal         = rand(1,Taille) - 0.5              ;
    Signal(1)      = 1                            ;
    Resultat_Dirac = filter(RI_dir,RI_rec,Signal) ;
    
    % Equation de récurrence gérée à la main + saturation
    Taille_signal         = size(Signal ,2) ;
    Taille_filtre         = size(RI_glob,2) ;
    Resultat_Dirac_manuel = zeros(1,Taille_signal) ;
    for i = 1:Taille
      Taille_conv              = min(Taille_filtre,i)                                                                                                                               ;
      Resultat_Dirac_manuel(i) = (sum(RI_dir(1:Taille_conv).*Signal(i:-1:i-Taille_conv+1)) - sum(RI_rec(2:Taille_conv).*Resultat_Dirac_manuel(i-1:-1:i-Taille_conv+1))) / RI_rec(1) ;
      Resultat_Dirac_manuel(i) = saturation(Resultat_Dirac_manuel(i),1)                                                                                                             ;
    end
    
    % Construction des sonagrammes
    [Amp        Freq Temps] = specgram(Resultat_Dirac       ,Nfft_sonag,Fech,Fenetre,Nrecouvr) ;
    [Amp_manuel Freq Temps] = specgram(Resultat_Dirac_manuel,Nfft_sonag,Fech,Fenetre,Nrecouvr) ;
    
    % Tracés
      figure(20) ;
      subplot(2,2,1) ;
      plot(t,Resultat_Dirac) ;
      subplot(2,2,2) ;
      plot(t,Resultat_Dirac_manuel) ;
      subplot(2,2,3) ;
      imagesc(Temps, Freq(1:2049,:), (abs(Amp       (1:2049,:)))) ;
      axis xy ;
      subplot(2,2,4) ;
      imagesc(Temps, Freq(1:2049,:), (abs(Amp_manuel(1:2049,:)))) ;
      axis xy ;

[phuphus]

... et un ch'tit bonus, une simulation où le système a accroché sur la composante continue ! Pas possible dans la réalité, sauf à construire un matériel et une salle dédiés, mais comme pour l'instant le modèle passe le continu...

[jeuxjeux]

Pas encore pu voir ton image, j'attends qu'elle soit approuvée, mais dans tous les cas, il n'est pas normal que l'on ai une fréquence nulle qui apparaisse, d'ailleurs, elle apparaît dans la plupart (tous) les tests, la modélisation est donc forcément fausse. Je vais regarder si en changeant la modélisation de la saturation, on peut obtenir quelque chose de plus correct.

A propos des conditions aux bords, est-ce que cette explication est valable :


Le noir représente la fréquence testée par la TF, en rouge, le signal à un instant donné, en vert, un autre instant.

A un moment, on a une amplitude de 1, à l'autre, de -1. A un moment, il a donc bien fallu passer par zéro (au temps entre les deux, les contributions positives compensent les négatives)

Est-ce une explication correcte de la périodicité observée lors de l'analyse fréquentielle que j'avais faite de prime abord? Si c'est le cas, afin d'éviter ce problème, que fait la fonction matlab? Si l'lgorithme fft est vraiment soumis à cette contrainte, elle n'a plus aucune valeur, car pour une configuration donnée, on aurait parfois (souvent), des fréquences qui n'apparaîtraient pas ou qui seraient représenté à une bien trop faible amplitude. Surtout que regarder le signal sur une plus grande fréquence ne change rien à ce problème.

La fonction "specgram" utilisé n'a pas ce problème, afin de l'éviter, comment fonctionne-t-elle? Fait elle une FFT en regardant à chaque fois le maximum d'amplitude obtenu pour un déphasage de la fréquence test? Peut-être n'ai-je pas compris le problème de bas ou en tout cas ses causes, mais si c'est ce que je présente, cela me semble particulièrement embêtant comme problème car pouvant fausser totalement un résultat.

Puis-je avoir des éclaircissement à ce propos?
Merci d'avance!

[jeuxjeux]

Bonsoir Phuphus,

Je vois que tu as corrigé ton code de l'image des fréquences correspondantes au test sans saturation, peux-tu me l'envoyé, afin que j'ai de beaux graphiques comme toi.

Sinon, j'ai changé la modélisation de la saturation :
function y = Saturation(x,sat)
y = min(abs(x), 0.8*sat+(2*sat)/(5*pi)* atan(((5*pi)/(2*sat))*(abs(x) - 0.8*sat)) ) *sign(x) ;

Ca fait cette belle courbe :


Donc jusqu'à 80% de la valeur, ça fait une belle ligne droite, puis après, cela suit la courbe d'une arctangeante, mais aussi bien la continuité de la fonction que celle de la dérivée première sont respectées. (on prend le minimum des courbes, et l'on voit aussi la valeur de la saturation choisie)

Sinon, j'ai aussi eu des résultats avec des saturations d'un côté, mais c'est totalement faux physiquement, c'est-ce pas? Donc, il va falloir arranger ça. Bon, encore un jour où je me couche trop tard.

[yellowstone44]

Pour moi, Si on veut s'imaginer visuellement ce qu'est est effet larsen, il suffit de le comparer à 2 miroirs que l'on mettrait en face à face. On observe alors l'image du miroir dans le miroir qui s’étend vers l'infinie en devenant de plus en plus petit. L'effet larsen correspond au même effet pour une onde sonore. Le micro envoie une onde dans le haut parleur qui retranscrit cette onde. Si le micro est placé à coté du haut parleur, il va capter de nouveau le premier son et le renvoyer indéfiniment aux HP.

Bon, je ne réponds pas à la question. C'était pour parler.

[phuphus]

Bonjour,

Pour moi, Si on veut s'imaginer visuellement ce qu'est est effet larsen, il suffit de le comparer à 2 miroirs que l'on mettrait en face à face. On observe alors l'image du miroir dans le miroir qui s’étend vers l'infinie en devenant de plus en plus petit. L'effet larsen correspond au même effet pour une onde sonore. Le micro envoie une onde dans le haut parleur qui retranscrit cette onde. Si le micro est placé à coté du haut parleur, il va capter de nouveau le premier son et le renvoyer indéfiniment aux HP.

Non, ça, c'est un écho, du nom d'une nymphe des sources et des forêts. Pour le Larsen, il faut une amplification.

[yellowstone44]

Bonjour,


Non, ça, c'est un écho, du nom d'une nymphe des sources et des forêts. Pour le Larsen, il faut une amplification.

OK, autant pour moi.

[phuphus]

Bonsoir,

Pas encore pu voir ton image, j'attends qu'elle soit approuvée, mais dans tous les cas, il n'est pas normal que l'on ai une fréquence nulle qui apparaisse, d'ailleurs, elle apparaît dans la plupart (tous) les tests, la modélisation est donc forcément fausse. Je vais regarder si en changeant la modélisation de la saturation, on peut obtenir quelque chose de plus correct.

L'apparition de la composante continue est normale puisque j'ai approximé la fonction de transfert du HP à celle d'une système masse-ressort en X/F. C'est avoué depuis le début dans mon code (relis mon intervention précédente), et parmi les améliorations citées dans ma première intervention, il y avait :

introduction de réponses impulsionnelles réelles

A propos des conditions aux bords, est-ce que cette explication est valable :
Pièce jointe 195846

Le noir représente la fréquence testée par la TF, en rouge, le signal à un instant donné, en vert, un autre instant.

A un moment, on a une amplitude de 1, à l'autre, de -1. A un moment, il a donc bien fallu passer par zéro (au temps entre les deux, les contributions positives compensent les négatives)

Est-ce une explication correcte de la périodicité observée lors de l'analyse fréquentielle que j'avais faite de prime abord? Si c'est le cas, afin d'éviter ce problème, que fait la fonction matlab? Si l'lgorithme fft est vraiment soumis à cette contrainte, elle n'a plus aucune valeur, car pour une configuration donnée, on aurait parfois (souvent), des fréquences qui n'apparaîtraient pas ou qui seraient représenté à une bien trop faible amplitude. Surtout que regarder le signal sur une plus grande fréquence ne change rien à ce problème.

Ce que tu décris avec tes courbes noire / rouge / verte est une onde stationnaire. Ce n'est pas l'objet ici. Tes artefacts sur ton tracé en mesh viennent juste du fait que tu regardes la partie réelle de la FFT, c'est tout.

La fonction "specgram" utilisé n'a pas ce problème, afin de l'éviter, comment fonctionne-t-elle? Fait elle une FFT en regardant à chaque fois le maximum d'amplitude obtenu pour un déphasage de la fréquence test? Peut-être n'ai-je pas compris le problème de bas ou en tout cas ses causes, mais si c'est ce que je présente, cela me semble particulièrement embêtant comme problème car pouvant fausser totalement un résultat.

Si tu prends la partie réelle de ce que renvoie specgram, il y aura les mêmes problèmes. As-tu essayé, comme je te le suggérais hier, d'enlever le "real" à la ligne suivante de ton progamme ?

Y(i+1,:) = abs(real(fft(Resultat_Dirac(di st*i+1:dist*i+L),NFFT)/L));

Je vois que tu as corrigé ton code de l'image des fréquences correspondantes au test sans saturation, peux-tu me l'envoyé, afin que j'ai de beaux graphiques comme toi.

C'est le code que j'ai publié hier ici :

http://forums.futura-sciences.com/ph...rsen-3.html#35

Sinon, j'ai changé la modélisation de la saturation :
function y = Saturation(x,sat)
y = min(abs(x), 0.8*sat+(2*sat)/(5*pi)* atan(((5*pi)/(2*sat))*(abs(x) - 0.8*sat)) ) *sign(x) ;

OK, nouvelle fonction intégrée à mon code ! L'apparition du Larsen a l'air plus progessive, et le Larsen plus "stable" avec cette fonction de saturation.

Sinon, j'ai aussi eu des résultats avec des saturations d'un côté, mais c'est totalement faux physiquement, c'est-ce pas? Donc, il va falloir arranger ça. Bon, encore un jour où je me couche trop tard.

Pas totalement faux, juste entaché des simplifications faites depuis le début.

Je te mets donc en PJ un pack contenant :
- le code mis à jour, avec sonagrammes d'amplitude (il manque l'échelle) et gestion d'une véritable réponse impulsionnelle d'ampli Marshall
- la fonction de saturation telle que tu l'as définie
- la réponse impulsionnelle d'un ampli Marshall 1960A + micro Neumann KM84 (donc plus de fréquence nulle)

Il y a encore quelques améliorations à faire (paramètres du sonagramme à mettre en variables, rééchantillonnage à la volée de la RI de l'ampli Marshall pour pouvoir changer sereinement Fech dans le programme, échelles du sonag, etc.)

Pour l'instant j'ai gardé le système masse-ressort dans le code, c'est juste que la RI_ms est écrasée à la ligne 60 par celle du Marshall.

La réponse impulsionnelle de Marshall a été téléchargée ici :

http://www.redwirez.com/

et j'ai pris la "Marshall1960A-G12Ms-KM84-Cap-12in.wav", que j'ai rééchantillonnée à 50 kHz.

Cette fois, le Larsen a l'air de converger à chaque fois vers une seule fréquence (+ les harmoniques impairs), il faudrait voir avec des RI d'autres amplis ou d'autres couples ampli + micro.

Bonne nuit !

[jeuxjeux]

Merci pour le code global, j'ai fait quelques tests comme tu pourras le voir dans la suite.

Tout d'abord, désolé Phuphus, j'avais zappé deux de tes messages, donc je t'ai fait répéter certaines choses.

Mis à part cela, j'avais en effet lu ceci :
% Critiques. 1 - On passe toutes les BF, alors que l'on devrait avoir une coupure d'ordre 2 (enceinte close) ou d'ordre 4 (bass-reflex).

Et ça n'avait pas été très clair. Mais maintenant que j'ai été regardé ce qu'était une enceinte close et bass-reflex, je comprend mieux. (Je ne comprend toujours pas pourquoi ça doit être d'ordre 2 ou 4, mais je veux bien te croire)

Une chose m’étonne encore, la gamme de fréquence énorme sur laquelle s’établi le Larsen, en effet, c’est sur un bon 300 Hz (jusque 500Hz), et pour une fréquence de 2500Hz, ça représente entre 12 et 20%. N’est-ce pas particulièrement élevé. Sans savoir vraiment ce que je faisait, j’ai changé les paramètres comme
Q = facteur de surtension, ça ne change rien (n’est-ce pas pourtant cela qui définit la précision fréquentielle de la résonance) , j’ai changé le gain, mais ça ne donnait rien, la constante de rappel et la masse. Seule un changement de la distance crée un (tout petit) changement sur la gamme de fréquence de la fréquence Larsen, et surtout, change les fréquences larsen.

Distance : de 0 à 0.06 m : 200-400 Hz (0.06 est la limite, car on a soit 200-400, soit 3150-3400 selon qu’il y ait ou non du bruit ambiant)
0.07-0.51 : 3150-3400 Hz
à 0,53, hésite entre 2350-2650 et 3050-3250 pour terminer sur la première citée
0,53-0,56 : 2250 à 2550 Hz
à 0,6025 plus d’effet Larsen mais tendance à voir apparaître entre 3150 – 3400

Il serait peut-être intéressant de faire les différentes fréquences qui apparaissent selon la distance.

Au fait, il y a un problème, car si je change la fréquence d’échantillonnage, les fréquences qui apparaissent dans le graphique de la fréquence en fonction du temps dépendent linéairement de ce changement (2x plus grande fr d’échantillonage, fréquence de Larsen affichée 2x plus grande).

Si je change la vitesse, il y a des changements, mais dont il semble difficile de trouver une dépendance simple.

Voilà, c’est ce que j’ai testé ce soir. Il y a peut-être d’autre chose à regarder. Mais ce qui m’étonne le plus, ce de ne pas avoir réussi à changer la précision fréquentielle de l’effet Larsen. C’est ma plus grande interrogation.

A+

[phuphus]

Bonsoir jeuxjeux,

Une chose m’étonne encore, la gamme de fréquence énorme sur laquelle s’établi le Larsen, en effet, c’est sur un bon 300 Hz (jusque 500Hz), et pour une fréquence de 2500Hz, ça représente entre 12 et 20%. N’est-ce pas particulièrement élevé.

L'analyse spectrale a un DeltaF de presque 100Hz, l'étalement est juste un biais d'analyse.

Sans savoir vraiment ce que je faisait, j’ai changé les paramètres comme
Q = facteur de surtension, ça ne change rien (n’est-ce pas pourtant cela qui définit la précision fréquentielle de la résonance) , j’ai changé le gain, mais ça ne donnait rien, la constante de rappel et la masse. Seule un changement de la distance crée un (tout petit) changement sur la gamme de fréquence de la fréquence Larsen, et surtout, change les fréquences larsen.

Le système masse-ressort est neutralisé à la ligne 60, lorsque j'écrase sa réponse impulsionnelle par celle du Marshall. Si tu veux faire mumuse avec le système masse-ressort, il faut mettre la ligne 60 en commentaire.

Distance : de 0 à 0.06 m : 200-400 Hz (0.06 est la limite, car on a soit 200-400, soit 3150-3400 selon qu’il y ait ou non du bruit ambiant)
0.07-0.51 : 3150-3400 Hz
à 0,53, hésite entre 2350-2650 et 3050-3250 pour terminer sur la première citée
0,53-0,56 : 2250 à 2550 Hz
à 0,6025 plus d’effet Larsen mais tendance à voir apparaître entre 3150 – 3400

Très intéressant le 0.6025 (il faut que j'essaye de mon côté). Cela va nous permettre de tester l'influence d'une paroi

Au fait, il y a un problème, car si je change la fréquence d’échantillonnage, les fréquences qui apparaissent dans le graphique de la fréquence en fonction du temps dépendent linéairement de ce changement (2x plus grande fr d’échantillonage, fréquence de Larsen affichée 2x plus grande).

C'est normal :

Il y a encore quelques améliorations à faire (paramètres du sonagramme à mettre en variables, rééchantillonnage à la volée de la RI de l'ampli Marshall pour pouvoir changer sereinement Fech dans le programme, échelles du sonag, etc.)

Avec le système masse-ressort réactivé, tu n'auras plus ça. Mais tu retrouveras notre bonne vieille composante continue, à moins de rajouter un passe-haut sur RI_ms (ordre 4 pour du bass-reflex !).

Voilà, c’est ce que j’ai testé ce soir. Il y a peut-être d’autre chose à regarder. Mais ce qui m’étonne le plus, ce de ne pas avoir réussi à changer la précision fréquentielle de l’effet Larsen. C’est ma plus grande interrogation.

Interrogation dissipée avec le présent message !

[jeuxjeux]

Bonsoir,
ça fait un petit temps, mais je n'ai pas vraiment eu le temps de répondre.

Je suis content, j'ai trouvé ce qui était la cause de la largeur de bande des fréquences de résonances, c'est le hanning. Je suppose que le hanning représente la fonction fenêtre. Plus elle est grande, et plus dans l'espace des fréquences, elle est étroite. Au contraire, plus elle est étroite, et plus le premier lobe des fréquences est large. C'est pour cela que quels que soient les changements fait au code, la largeur de la fréquence de résonance était toujours semblable. En changeant le nombre de point de la fonction fenètre par contre, on peut augmenter grandement la précision de la valeur de la fréquence de résonance (j'ai mis Nrecouvr = 4000; et Fenetre = hanning(4096); plutôt que 500 et 512.

Dans mon souvenir de l'un de mes cours, si la fenêtre était plus longue, il y avait néanmoins un problème sur les lobes secondaires qui étaient importants, mais je ne vois rien de tout cela. Qu'en est-il?

Pour ce qui est des résultats, je suis tombé sur un truc intéressant.
1) la fréquence de Larsen semble toujours être un peu différente. (pour pouvoir voir ces faibles variation, il faut une meilleure précision spectrale, et donc une fenêtre de hanning comprenant plus de points)
2) sans bruits, le signal est stable à une fréquence, n'importe laquelle si elle est maximum locale de la boucle. Mais avec du bruit, on obtient une variation en fréquence de l'ordre de la vingtaine de Hz (dans le cas présent, voir figure jointe). On peut aussi augmenter le bruit et voir si la fréquence de Larsen est plus régulière. A mon avis, plus le bruit est conséquent, et plus l'effet Larsen ne pourra apparaître que sur des fréquences spécifiques. Si le bruit est très faible, tout maximum local est suffisant.

Voici quelques images pour se faire quelques idées :
distance01.jpg

distance03.jpg

grand_bruit.jpg

A+

[phuphus]

Bonsoir jeuxjeux,

Je suis content, j'ai trouvé ce qui était la cause de la largeur de bande des fréquences de résonances, c'est le hanning.

C'était (implicitement) dit dans ma précédente réponse, où je parle de DeltaF égal à 100 Hz. Désolé si cela n'était pas assez clair. A nuancer toutefois : le zero-padding, en interpolant en fréquentiel, permet de détecter beaucoup plus finement que cela le maximum grâce aux points adjacents.

C'est pour cela que quels que soient les changements fait au code, la largeur de la fréquence de résonance était toujours semblable.

Pas vraiment, dans ton intervention précédente c'était parce que le facteur de qualité n'avait plus rien à voir avec la réponse impulsionnelle. Dans tous les cas, une fenêtre plus grande te permet une plus grand précision fréquentielle, mais une plus faible précision temporelle.

En changeant le nombre de point de la fonction fenètre par contre, on peut augmenter grandement la précision de la valeur de la fréquence de résonance (j'ai mis Nrecouvr = 4000; et Fenetre = hanning(4096); plutôt que 500 et 512.

Attention toutefois en faisant cela au côté "temps-fréquence". Un signal de 0.2s à 50 kHz fait 10 000 points. Si tu fais une analyse spectrale glissante sur 4096 points (presque la moitié de ton signal !!!), autant faire un spectre de 10 000 points tout court. Au moins, tu auras la précision max sur la fréquence.

L'image jointe a été faite avec du 512, on voit parfaitement les changements mineurs de la fréquence du Larsen via l'influence du bruit blanc. Le zero-padding à 16384 points est justement là pour ça.

2) sans bruits, le signal est stable à une fréquence, n'importe laquelle si elle est maximum locale de la boucle. Mais avec du bruit, on obtient une variation en fréquence de l'ordre de la vingtaine de Hz (dans le cas présent, voir figure jointe). On peut aussi augmenter le bruit et voir si la fréquence de Larsen est plus régulière. A mon avis, plus le bruit est conséquent, et plus l'effet Larsen ne pourra apparaître que sur des fréquences spécifiques. Si le bruit est très faible, tout maximum local est suffisant.

Ça, c'est intéressant. Je pense qu'en venant s'additionner au signal bouclé, la présence du bruit blanc modifie légèrement les relations de phase autour de la fréquence du Larsen au micro (puisqu'on peut voir un bruit blanc comme une addition de fréquences dont la phase varie aléatoirement), c'est ce qui fait légèrement glisser le Larsen.

Je vois que tu t'amuses bien, j'espère que le programme répond à tes attentes

[jeuxjeux]

Merci à tous pour vos contributions, et particulièrement à Phuphus qui est allé dans la direhttp://forums.futura-sciences.com/newreply.php?p=4204390&noquote =1ction qui m'intéressait (et a pu rendre beau sous matlab un code assez débutant que j'avais fait) ! J'ai appris plein de chose et vais certainement pouvoir en réutiliser de nombreuses. Le code n'est pas parfait, il y a encore des erreurs ou en tous cas des approximations, mais je suis très content de tout ce que j'ai appris.

Encore merci à tous,
A la prochaine !