Bonjour,

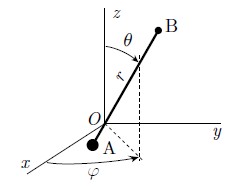
Je rencontre un petit problème en physique statistique, à propos du gaz parfait de molécules diatomiques. On s'intéresse uniquement à la rotation interne de la molécule. Le schéma suivant indique comment elle est modélisée, dans le référentiel de son centre de masse O :

Nom : molécule diatomique.jpg Affichages : 35 Taille : 6,6 Ko

Après une petite étude mécanique, on montre que le hamiltonien associé à la rotation propre de la molécule est :



où I est le moment d'inertie de la molécule par rapport à son centre de masse. On calcule alors la fonction de partition associée :



et on trouve :



Jusque là, tout va bien. Après ça, on me demande d'exprimer la densité de probabilité dans l'espace des phases. Sauf erreur de ma part, elle doit s'exprimer ainsi :



Je dois ensuite déterminer la probabilité que la particule soit orientée selon la direction . J'intègre donc la densité de probabilité pour et sur pour les impulsions. L'intégration sur et sur donne :



soit, en intégrant sur :



Et c'est là que ça coince Je ne vois pas bien où j'ai pu me tromper, mais ce résultat va à l'encontre de l'isotropie de l'espace, puisque certaines orientations de la molécule seraient plus probables que d'autres J'aimerais bien savoir où j'ai fait une erreur, ou, si ce n'est pas le cas, pourquoi ce résultat serait correct. Merci de votre aide