Bonjour,
Je bloque sur cette question : Calculer la puissance fournie par l'eau à la turbine.
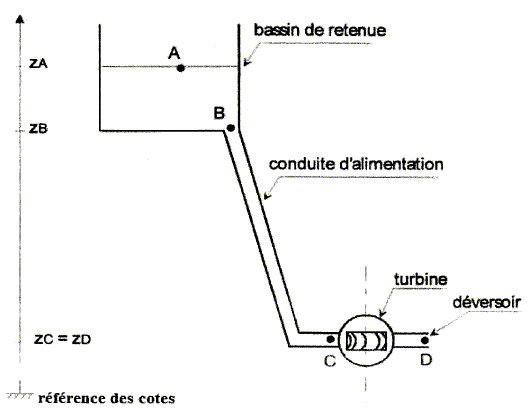
Une turbine est alimentée par une retenue d'eau selon le schéma ci-dessous :
Sachant que :
- diamètre d de la conduite d'alimentation et du déversoir de section circulaire : d = 0,7 m
- pressions aux points A, C et D : pA = pD = 1,01 bar ; pC = 1,10 bar
- cote des points A, B et C par rapport à une origine de référence : zA =363 m ; zB=361 m ; zC= 353 m
- masse volumique de l'eau r=1,00 103 kg m-3
- intensité de la pesanteur g = 9,81 m s-2. 1 bar = 105 Pa.
vc=13,3 m/s
Qv=5,13 m^3/s
vc=vb
pb=3,15*10^4 Pa
vd=0 m/s
l'eau sera considérée comme [url]un fluide parfait incompressible. On supposera que le niveau de l'eau dans la retenue est constant.
On rappelle la relation de Bernoulli entre deux sections d'écoulement d'un tube de courant :
½r (v12-v22) +rg(z1-z2) +p1-p2 = Pext/Qv
Tout d'abord, j'aimerai savoir s'il y a une importance quand à l'ordre des points, en cours mon prof avait dit qu'il fallait toujours mettre le point le plus haut en premier, sauf que là les points sont à la même hauteur, mais après ça change au niveau de la valeur trouvée:
lorsque j'utilise la relation en mettant : 1/2r* (vc²-vd²)+rg(zc-zd)+pc-pd=Pext/Qv , j'obtiens une valeur positive alors que c'est une turbine donc je dois trouver Pext<0.
Je voulais aussi savoir qu'elle était la vitesse au point c, 13,3 m/s ou 0 m/s , car vs=0 m/s et étant donné que l'on est dans un tuyau horizontal de même diamètre, j'aurai tendance à dire que vc=vd soit 0m/s.
Ce qui fait que le calcul se résumerait à : Pext=Qv*(pd-pc)=5,13*(1.01*10^5-1,1*10^5)=-46,2 kw.
Merci d'avance pour vos éclaircissements.
-----