saturation d'une équation et lien avec une autre EDO

[membreComplexe12]

Bonjour tous,

je ne savais pas trop comment appeler mon problème donc désolé pour le titre pourris

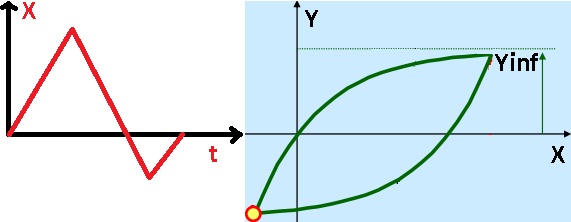
(dans le texte ci dessous "y" est la variable qui représente mon phénomène et "x" est une variable dont je peux connaitre l'évolution.
toutes les lettres majuscules A,B,C,D... sont des contantes)

Petite introduction :

1°) j'ai un phénomène physique un peu particulier (très très long à expliquer) qui se modélise très
bien avec une équation de cette forme :
Ctte équation est en fait postulée car on a remarqué qu'elle représenter super bien les phénomènes
que l'on voulait mais on est pas arriver à trouver une démonstration et c'est pour cela que je me permets de vous contacter
pour avoir des pistes.

2°) pour démontrer 1°) il faut nécessairement partir d'une équation tel que :
avec "z" une variable qui a une forme comme ceci :

Ce que je cherche :

3°) je cherche une fonction qui me permet d'avoir la variable "z" qui tend vers une constante "z*" lorsque "x" tend vers l'infini

4°) le 3°) est assez facile à respecter car si je prends ça fonctionne. Le seul soucis est que j'ai une autre condition à respecter
assez compliquée : si j'introduis l'expression de "z" dans l'équation "y=A.B.z" je dois arriver à retomber sur l'expression de départ 1°)

voyez vous quelle forme d'équation il faut pour afin de respecter ceci ?

merci pour les conseils/aide que vous pourrez m'apporter
-----

[kalish]

Bonjour, j'ai un peu de mal à saisir le 4°) et ce que tu demandes, en plus j'aurais une question: tes y et x dépendent d'un paramètre, mettons qu'on l'appelle s, puisque tu écris y point, et x point (flemme de latex).
Dans ce cas, quand tu écris y= A.B.z, tu ne dis pas si z, A, ou B dépendent de s.
C'est ennuyeux. Si z dépend de x, dépend-elle aussi de s directement/explicitement, en plus de dépendre de s par x? Je ne suis pas sûr que ta notation impliquant des dérivées partielles avec x soit très correcte. Il faudrait pour cela par exemple que z dépende de x, y, et s éventuellement, ça ne me parait pas clair dans ta notation.
Je ne vois pas comment tu arrives à dire que "ça marche" avec 1-z/z*. Ce que ça te dit c'est que si z tend vers z* quand x tend vers l'infini, alors phi tend vers 0.

Bref, il faudrait que tu réécrives ton énoncé un peu plus clairement au niveau mathématique même si on voit bien qu'il y a un bon effort de présentation concernant l'énoncé (faute de conjugaison et accords mis à part).

[membreComplexe12]

Bonjour Kalish et merci d'avoir pris le temps de répondre !

En effet je n'ai pas été très clair sur les variables, voici :
- dépend
- dépend de
- dépend de

D'accord, je vais essayer de lister les étapes peut être que se sera plus clair que mon texte :
1) je dois partir de cette équation
2) postuler une équation d'évolution pour qui à la forme
3) ensuite, si j'introduit 2) dans 1) alors je dois pouvoir retomber sur l'équation de départ :

La question clef est quoi choisir pour ?
la seule chose que je dois respecter pour le choix de c'est que ma variable tende vers une constante
dite de saturation si "x" tend vers l'infini

si je prends par exemple mon équation d'évolution est
est la solution de cette équation différentielle est :


Si tend vers l'infini j'ai bien ce que je cherche mais par contre si j'introduit cette solution
dans l'équation 1°) alors je ne retrouve pas l'equation 3°)

[kalish]

Salut, je vais y réfléchir, mais j'aurais une autre question y dépend de x, et x dépend de t, est-ce que y a une dépendance en t explicite, cad est-ce que y=y(x(t),t) ou y=y(x(t)), qu'est-ce que tu entends par y point? est-ce que c'est d y /dt ou dérivée partielle par rapport à t, ou dérivée partielle par rapport à x... encore une fois tu emploies la même notation.
Et A B sont des constantes?

[A voir en vidéo sur Futura]

[membreComplexe12]

Salut, je vais y réfléchir

merci Kalish de prendre le temps de m'aider !

y dépend de x, et x dépend de t, est-ce que y a une dépendance en t explicite, cad est-ce que y=y(x(t),t) ou y=y(x(t)),

oui "y" depend de "x" mais il n'y a pas de dépendance explicite entre "y" et "t"
donc

qu'est-ce que tu entends par y point? est-ce que c'est d y /dt ou dérivée partielle par rapport à t, ou dérivée partielle par rapport à x... encore une fois tu emploies la même notation.

Désolé pour cette imprecision, lorsque je note ça signifie :
en fait à chaque fois que je mets alors ce "qqch" est dérivé par rapport au temps.

Et A B sont des constantes?

Oui, de même pour C et D.
Les seuls choses variables sont "y" "x" "z" et le temps "t"

[kalish]

Si tu n'as pas de dépendance explicite en t alors la notation n'est pas justifiée. En règle générale pour y(x(t),t), on aura
et y m'a tout l'air d'être une fonction, une fonction qui varie certes, comme pas mal de fonctions, mais je ne l'appellerais pas variable. Comment veux tu dériver uniquement par rapport au temps, si tu n'as pas de dépendance en temps. Donc si tu as juste y(x(t)) tu as
et la dérivée partielle dans ce cas là est encore un peu abusive ou superflue.
Comme z = y à une constante près tu dois pouvoir réinjecter ce que tu sais sur z là dedans.
La fonction (2z*/pi) arctan(x) tend vers z* quand x tend vers l'infini, mais il y en a pas mal des fonctions comme ça.

[kalish]

si on reprend ton problème alors:

donc

en réinjectant ça dans l'équation que tu dois vérifier, tu peux trouver que
, donc quand et l'équation devient

soit donc finalement je ne voit pas trop ce que vient faire , ni z là dedans, mais tu peux les retrouver à partir de y.

[membreComplexe12]

je vois ce que tu veux dire kalish merci !

par contre dans le cas où alors je ne vois pas trop comment faire car lors de la résolution je vais
avoir un terme que je ne sais pas intégrer...

pourrais tu me dire ce que ça fait dans le cas négatif comme résultat ?

merci bcp

[kalish]

Ben je ne sais pas ce que tu veux intégrer et dans quel cas, je ne sais même pas si je t'ai aidé parce que comme je t'ai dit TA question portait sur phi, et on en a pas trop besoin dans ce que j'ai fait, donc il doit me manquer quelque chose. Par contre si alors et l'équation se résoud de la même manière, le soucis c'est que la solution ne tend pas vers une constante quand x tend vers l'infini.

[membreComplexe12]

en fait j'avais un peu trop la tête dans le guidon et je pense que tes messages mon permis d'avoir un oeil un peu plus critique sur mon problème.
Je suis en train de me reposer les bonnes questions car ils y a quelques trucs qui sont un peu flou de mon côté.

je vais tirer ceci au clair et je te tiens au courant au plus vite pour faire un point lorsque j'aurais les idées plus au claires.
merci pour tout,à bientôt

[kalish]

ok pas de soucis, moi aussi ça m'arrive, et à ce qu'il parait c'est le plus important!( ne pas avoir le nez dans le guidon)

[membreComplexe12]

kalish, je viens de reprendre l'équation différentielle de départ et il y a bien une solution dans le cas général qui est :



avec si et si

du coup, à présent il faut que je trouve une équation d'évolution pour qui me permet de retomber sur cette expression
pour "z" (àune une constante près)

[kalish]

C'est quoi v? Forcément si tu introduis une constante tu peux retomber sur un cas où ton exponentielle tend vers 0 quand x tend vers l'infini. Ensuite je ne comprends pas trop ta remarque, il n'y a pas de différence entre z et y, z=y à une contante multiplicative près... donc pour trouver dz/dx tu dérives juste y... ce qui fait juste une exponentielle. Il faut que dz/dx = 0 à l'infini puisque z tend vers une constante, et c'est bien le cas avec cette expression.

[kalish]

Autrement dit si

alors Mais il y a surement une subtilité dans ton problème qui m'échappe car je ne vois pas à quoi sert Phi, donc je ne suis pas sûr que tu l'aies bien exposé, par exemple concernant x point on a considéré qu'il était soit positif soit négatif, mais si ça varie au cours du temps alors c'est plus problématique. Ton problème me fait penser à une histoire de condensateur qu'on charge et qu'on décharge.
Et tu as fait une erreur dans ta solution "générale", la solution est en et pas en , donc elle ne tend pas vers une constante.

[membreComplexe12]

désolé si je me suis mal exprimé :

- au départ j'ai cette équation "référence" que j'apperai (1)

maintenant je dois trouver une expression pour tel que (2)

- du coup, ce que je me suis dis, c'est que si je trouve la solution de l'equation (1) (que j'ai noté dans mon message précédent) alors sera égale à

et du coup sera la même expression que (1) à un facteur près.

-> donc la solution de mon problème est :

ou quelque chose dans ce genre...

ps: pour trouver la solution que j'ai noté pour "y" j'ai fais deux résolutions différentes : le cas où donc
et le cas où donc et ça me donne deux solution différentes que je peux exprimer de la même manière
en introduisant une constante"v" qui vaut soit -1 soit 1 suivant le signe de

[membreComplexe12]

Pour être un peu plus précis voici comment j'ai trouvé la solution que je t'ai montré :
1°) dans le cas où j'ai positif je trouve ceci comme solution :



2°) dans le cas où j'ai négatif (donc x<x_0) je trouve ceci comme solution :



Donc au final je peux résumer par cette equation :



avec v qui est soit 1 soit -1

[kalish]

Malheureusement plus tu expliques et moins je comprends, je croyais que était une dérivée par rapport au temps, dans ce cas là, comment diable arrives tu à ton équation avec ??
tu viens de me mélanger et ,

[kalish]

et si ta constante v est négative et que tu prends une solution en exp(-vx) alors comme - par - ça fait plus, ta solution tend vers l'infini quand x tend vers l'infini.

[membreComplexe12]

Malheureusement plus tu expliques et moins je comprends, je croyais que était une dérivée par rapport au temps, dans ce cas là, comment diable arrives tu à ton équation avec ??
tu viens de me mélanger et ,

je crois bien que tu as raison... il me semble que j'ai mélangé et
mais maintenant que j'ai la solution de "y" ça devrait être simple de trouver la forme de qui permet de retrouver non ?

et si ta constante v est négative et que tu prends une solution en exp(-vx) alors comme - par - ça fait plus, ta solution tend vers l'infini quand x tend vers l'infini.

si ma constante "v" est négative ça veut dire que est un nombre négatif par définition.
J'ai v=-1 si négatif, donc si négatif
J'ai v=1 si positif, donc si positif

[kalish]

ah bon, je ne savais pas que quand \dot x < 0 ça entrainait que x-x_0 <0, tu peux en dire plus sur ce que tu modélises physiquement? à noter que la dérivée partielle par rapport au temps est la dérivée "locale" en général physiquement, juste une parenthèse.

mais maintenant que j'ai la solution de "y" ça devrait être simple de trouver la forme de qui permet de retrouver non ?

C'est ce que j'essaie de te dire, je dois avoir mal compris quelque chose parce que je ne vois pas l'intérêt de Phi dans ton problème.

[membreComplexe12]

ah bon, je ne savais pas que quand \dot x < 0 ça entrainait que x-x_0 <0, tu peux en dire plus sur ce que tu modélises physiquement?

en fait est une déformation. Si je compresse mon materiau, ça veut dire que je part d'un état initial qui est plus déformé que l'état actuel donc est négatif.
Et si c'est l'inverse.

"y" est une variable interne à de matériau qui est lié à une autre variable "z" dite de saturation. c'est vraiment très long à expliquer...

C'est ce que j'essaie de te dire, je dois avoir mal compris quelque chose parce que je ne vois pas l'intérêt de Phi dans ton problème.

peut etre que c'est moi qui m'embrouille, Phi n'est peut etre pas utile....

- en fait je sais que si je déforme beaucoup mon matériau positivement la variable "z" tend vers "z*"
et que la loi que je choisis pour cette évolution doit être en accord avec la loi d'évolution de Y que je connais.
Comme il doit y avoir saturation pour "z" alors je me suis dis que je dois avoir une fonction "Phi" qui permet de saturer "z" mais peut etre
que l'on est pas obligé de passer par ce Phi...

[kalish]

ah ok, ben c'est bon alors, non?

[membreComplexe12]

je pense que c'est un peu prêt bon à présent, merci beaucoup.

par contre j'ai une dernière question car j'ai du mal à interpréter ce genre de systeme...

Si j'ai une courbe d'entrée du système x=f(t) comme en rouge sur la pièce jointe
alors mon système réponds comme ceci y=f(x) (courbe en vert)



Ce que j'ai du mal à comprendre c'est que la réponse n'est pas symétrique :

--> si je fais une charge non symétrique la réponse du système revient à 0...