Experience de la pensée equivalence masse energie
Bonjour,
C'est un exercice que j'ai tiré des examens antérieurs que je suis en train de tous faire :
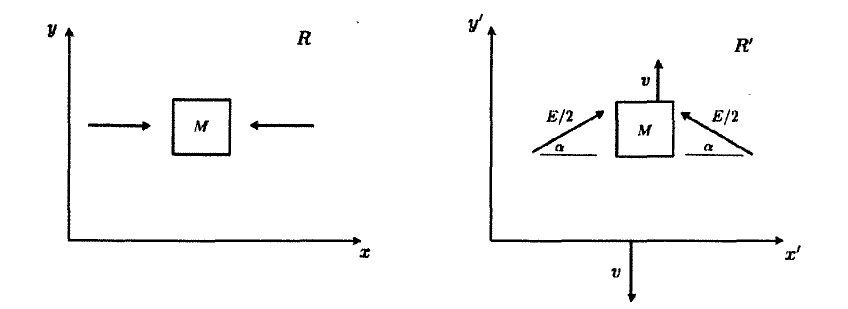
Considérez l'expérience de la pensée suivante pour dériver la fameuse équation d'Einstein qui
exprime l'équivalence entre l'énergie et la masse. Soit une masse M au repos dans R. Deux
photons d'égale énergie entrent en collision simultanément avec la masse ; elle
demeure au repos après la collision et sa masse augmente légèrement. Considérez cette même
expérience du point de vue d'un observateur dans R' qui se déplace avec une vitesse v selon
-y. Pour cet observateur, la masse se déplace avec une vitesse v selon +y' et les photons,
chacun d'énergie E/2 dans R', se propagent avec un angle a selon x' tel qu'indiqué sur la
figure. La masse est M' après absorption des deux photons. Démontrez que E = \DeltaM*c² où
\DeltaM =M' M. Faire l'hypothèse que la vitesse du référentiel est non-relativiste (v<< c).
Je pense qu'il faut utiliser la conservation de l’énergie et de l'impulsion
2E+M*c²=y*M'*c²+2(E/2)
E+M*c²=y*M*c²
On a que l'impulsion initiale Pi=0
Selon x:
E/2*cosa+E/2cosa=E*cosa=0v..?
Selon y
E*sin a + y*M'*v*c=0
Je pense avoir mes équations toutes fausses et je ne sais pas comment m'y prendre, si on peut m'expliquer les étapes, svp, mon exam est mardi si je ne réussis pas cet exo je vais stresser plus...
-----
Envoyé par ailita94 