Bonjour,
J'ai un exercice de mécanique niveau "approfondi" sur lequel je bloque.
Lors d'une descente à ski, le skieur est freiné par les frottements de l'air sur son corps et le frottement solide de ses skis sur la neige. L'inclinaison de la pente est 0=40°, la neige a un coefficient de frottement cinétique mu=0.0380, la masse du skieur et de son équipement m=85 kg. La section efficace du skieur (en position de shuss) est A=1.30m², le coefficient de traînée est C=0.150 et la masse volumique de l'air est p=1.20kh/m^3.
1. Quelle est la vitesse atteinte par le skieur ?
2. Si le skieur était capable de faire varier son coefficient de traînée C d'une petite quantité dC en ajustant par exemple la position de ses mains dans le shuss, quelle serait la variation correspondante de sa vitesse limite ?
Donc, avec de l'aide, on en a déduit que le bilan des forces était égal à f+R+P=0 avec f=frottements de l'air+frottements de la neige.
On a donc f(air)=-C.A.p.V² et f(neige)=-mu.Rn
On a donc -mu.Rn.(-C).A.p.V²+m.g+Rn=0 (c'est juste ?)
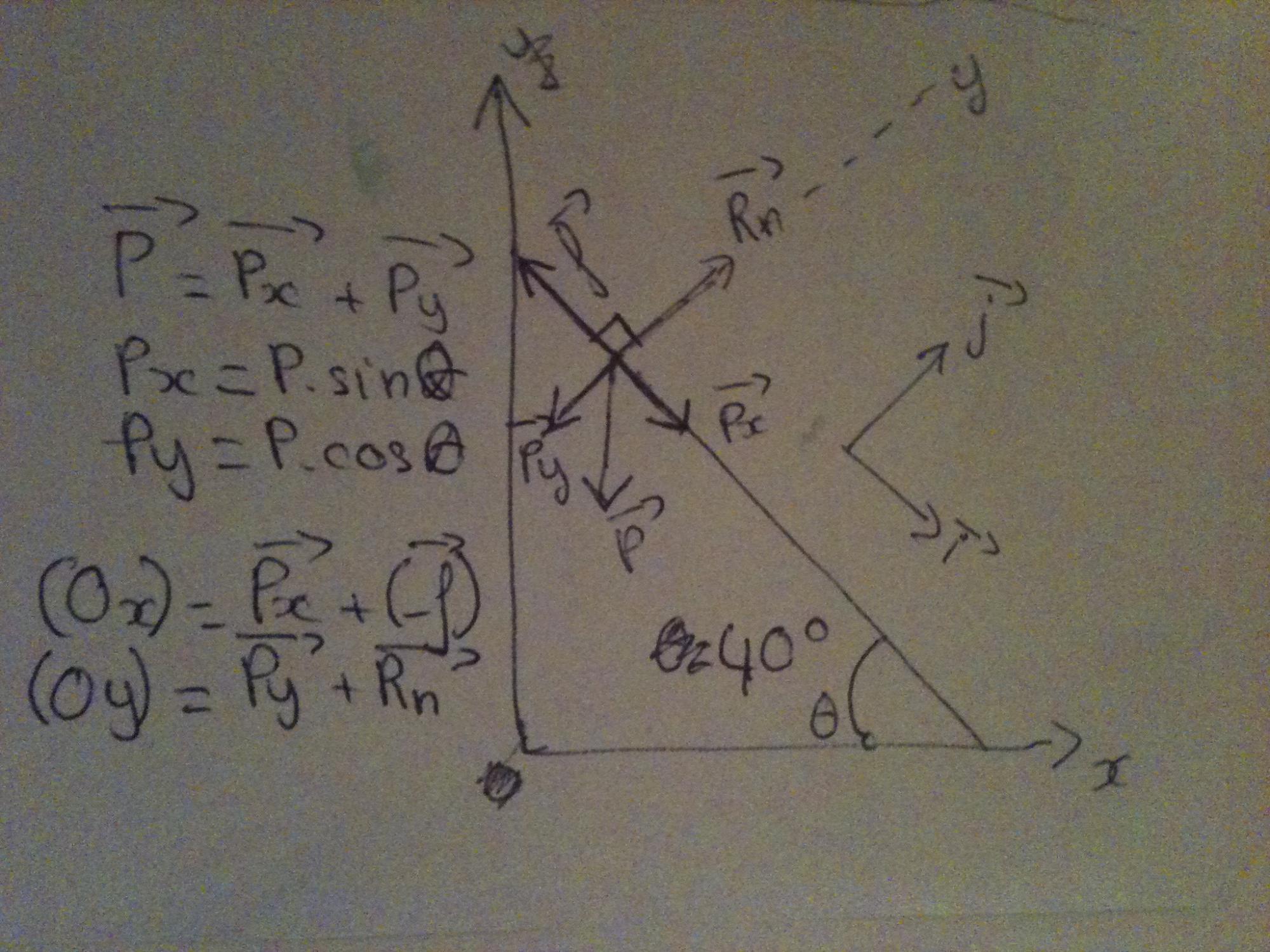
J'ai fait un schéma, avec la pente inclinée de 40° par rapport à l'axe des x, le vecteur force Rn perpendiculaire à la pente vers le haut (et au sens du mouvement), le vecteur des frottements f opposés au mouvement du skieur, et le vecteur du poids P parallèle à l'axe des y vers le bas.
Seulement, je suis bloquée pour la projection sur mes axes, et je voudrais également savoir si j'avais juste pour l'instant... Qui pourrait me donner une piste ?
Merci !
-----