Bonjour!
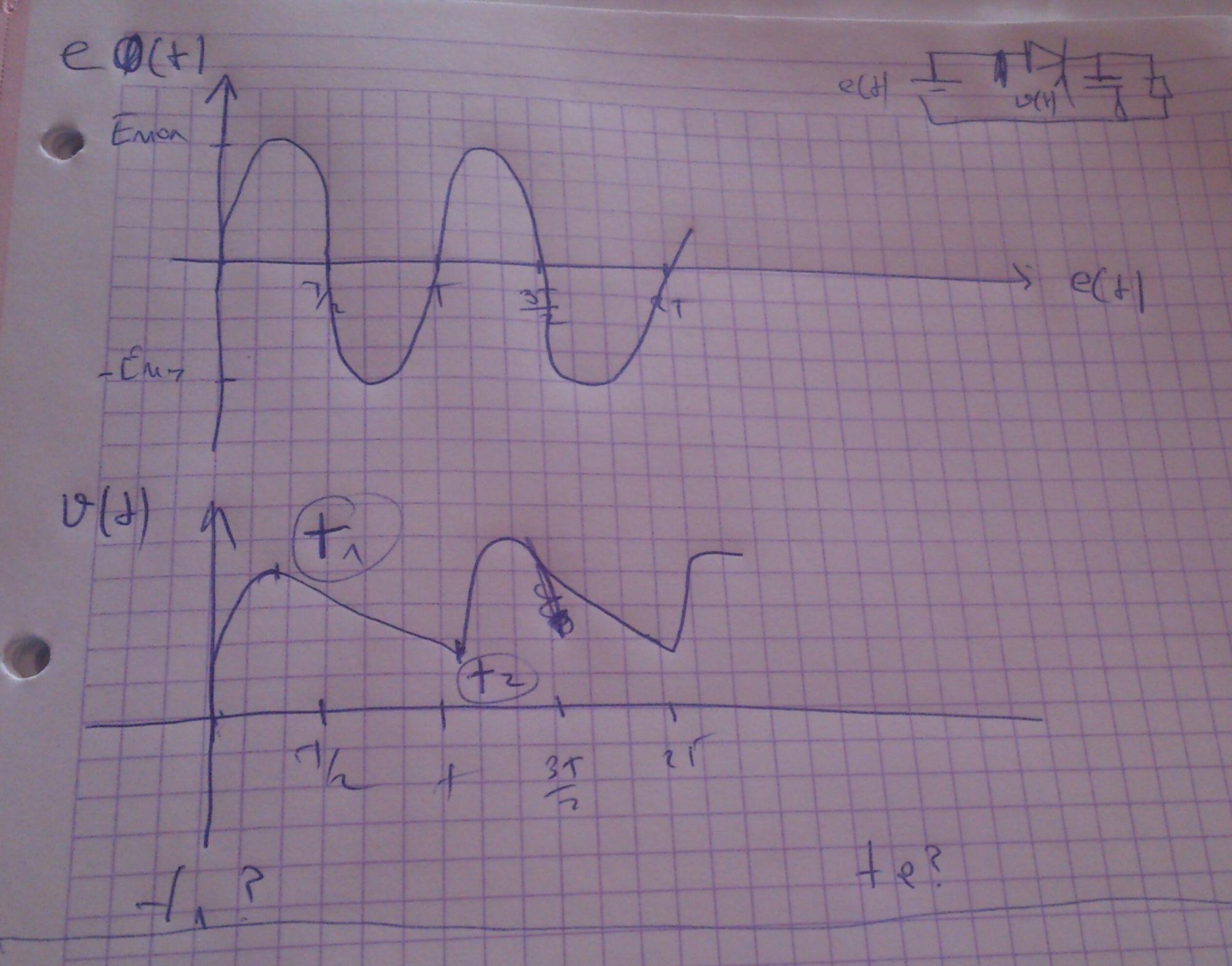
j'ai une signal E(t) = Emax.sin(wt) avec w= omega
je veux les cordonnés de changement de courbure du signal V(t) avec v(t) signal au bornes du condensateur(parallele au resistance R)..
c'est-a-dire: je veux savoir t1 et t2, et v(t1) et v(t2)
Aidez moi s'il veut plait!
Bonjour.
Il suffit d'écrie l'équation de la tension sinusoïdale et celle de l'exponentielle décroissante et trouver la valeur du temps pour laquelle les deux courbes se croisent.
Malheureusement, le résultat est une équation transcendante. C'est à dire que vous ne pourrez pas écrire t = ....
Vous ne pouvez trouver les valeurs de t que numériquement (ou graphiquement).
Il faut faire des approximations.
S'il s'agit d'un vrai montage redresseur, la tension au temps T2 est proche du maximum (et celle au temps T1 aussi) et les approximations sont justifiées.
L'approximation la plus courante est de considérer que le temps T1 correspond au maximum de la sinusoïde.
Pour calculer T2, on calcule la tension de l'exponentielle (que souvent on approxime par une droite) au temps correspondant au maximum de la sinusoïde.
Et avec cette tension on calcule le temps T2.
Depuis le temps que vous participez à ce forum, on doit vous avoir expliqué que "je veux" ne sonne pas très poli en français. Ça ressemble à un ordre donné à un servant. Utilisez plutôt "je voudrais", "je souhaite connaître", "je cherche".
Au revoir.
Je vous remercie @LPFR,
j'ai essayé de faire ce que vous m'avez dit!
Premièrement, a t1 v(t) > e(t) car l'exponentielle décroit lentement par rapport au sinus, donc la diode est bloquer
le courant générale i= ic + ir
on a diode bloquer donc i = 0 -> ic = -ir
voila ce que j'ai trouver
Comme vous voyez, t1 = -arctan(RCW) / W avec w = omega
on a t1 < 0, la j’obtiens t1 presque -1/w
j'arrive pas a comprendre ce que j'ai fais mal!
Passant a t2, on doit trouver la fonction exponentielle = la fonction Sinus au moment t2 Donc
Vexp(t2) = Vsin(t2)
Emax.sin(wt2).exp((t2-t1) /RC) = Emax sin (wt2)
donc, on obtient exp((t2-t1) /RC) = 1 ---------> (t2-t1) /RC = 0 ---> t2 = t1
il y a une erreur ici, s'il vous plait aidez moi
Re.
Vos calculs sont trop compliqués. Et je ne sais pas ce que vous essayez de calculer. Les formules exactes ? Les approximations ?
La première chose est de se simplifier la vie en changeant l'origine su temps au sommet de la sinusoïde.
Du coup, la tension est Vm.cos(wt).
Et l'exponentielle est (au peut près) Vm.e^(-t/tau).
Ceci correspond à dire que l'exponentielle commence au sommet du cosinus, ce que n'est pas exact mais qui est une approximation valable.
Si ce que vous voulez faire est trouver les formules exactes, alors, pour T1 il faut regarder quand la pente du cosinus et plus négative que la pente de l'exponentielle. Car c'est à ce moment que la diode se bloque.
Mais surtout, quoi que vous fassiez, c'est sur les courbes qu'il faut travailler. Par sur des équations des courants et compagnie.
A+
Merci a vous, j'arrive pas a comprendre quand la diode se bloque..Envoyé par LPFR
et pour T2 comment on fait pour la calculer?
Bonjour,
Si vous expliquez votre intention à chaque ligne, il serait plus facile de comprendre ce que vous faites
1) Tout t = 0 la source E = sinWt =0
2) pour wt = PI /4 , E = Emax , la tension au bornes du condensateur est Emax
Le courant durant la phase de 1 à 2 le courant alimente le condensateur et le résistance
3) a partir temps wt = Pi /4 la tension de la source diminue, le condensateur alimente la résistance
la tension aux bornes de la résistance ( ou du condensateur ) V = Emax exp ( -t /RC ) et le courant ir = V/R
4) le condensateur sera realimenté au temps t' telque ( condition de déblocage de la diode )
Emax sin wt' >= Emax exp ( t' /RC ) ==> sin wt' = exp ( t' /RC ) d'ou t'
Remarque, il y a une approximation au point 2, Si R est faible, il faut chercher t" tel que Emax sin WT"< Emax exp (-t" /RC ) condition de blocage de la diode
En science " Toute proposition est approximativement vraie " ( Pascal Engel)
