Bonsoir,
Je cherche à calculer (numériquement) la déformation des lignes de champs magnétiques à proximité d'un objet ferromagnétique.
Je suis parti du principe de superposition, et de diverses formules glanées ci et là sur la toile.
J'ai donc considéré le champ produit par une spire de courant, et un cube ferromagnétique posé sur l'axe de la spire. On connait l'excitation en tout point de l'espace par Biot et Savart. Je connais donc le vecteur aimantation au sein du ferromagnétique (M=chi*H) qui est supposé être un matériau magnétique parfait.
Maintenant les choses se "compliquent".
On a pour un volume élémentaire de ferromagnétique dm=chi*H*dV où H peut être considéré uniforme à cette échelle, où H est l'excitation, chi la susceptiblité, dm le moment magnétique et dV le volume.
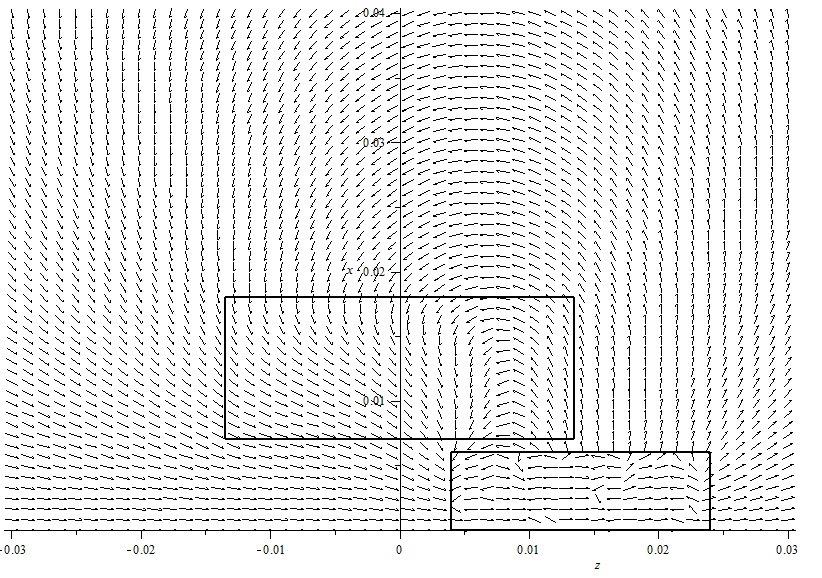
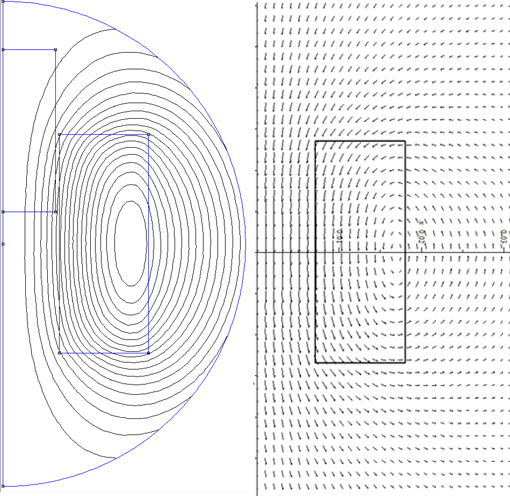
Et là je sèche. J'ai tenté de considérer chaque volume élémentaire comme un dipôle magnétique enfin de calculer un champ élémentaire dB (en galérant sur les changements de bases) puis intégrer sur le volume, mais le résultat n'est pas particulièrement concluant lorsque je compare le tracé du champ magnétique à celui produit par d'autres programmes expressément conçus pour l'étude de ces phénomènes...
J'aimerai donc avoir votre avis sur la question, quelles sont les équations à prendre en compte ?
Peut-être aurais-je du considérer le potentiel-vecteur, intégrer, puis calculer son rotationnel ?
L'erreur est-elle de considérer chaque élément infinitésimale comme un dipole magnétique ?
Merci !
-----





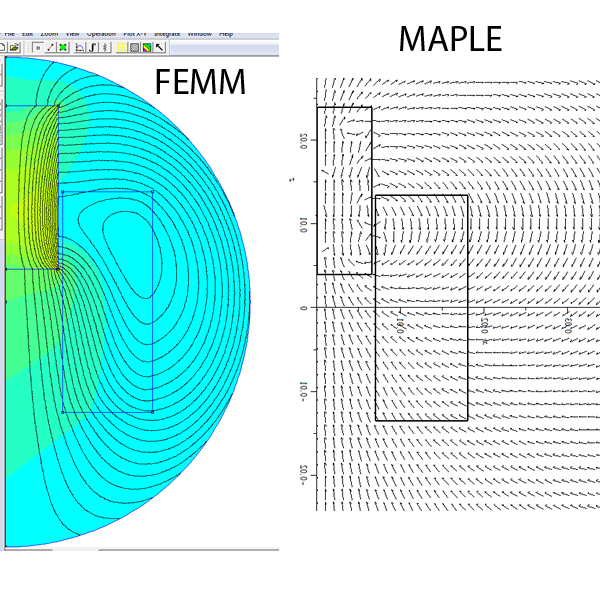
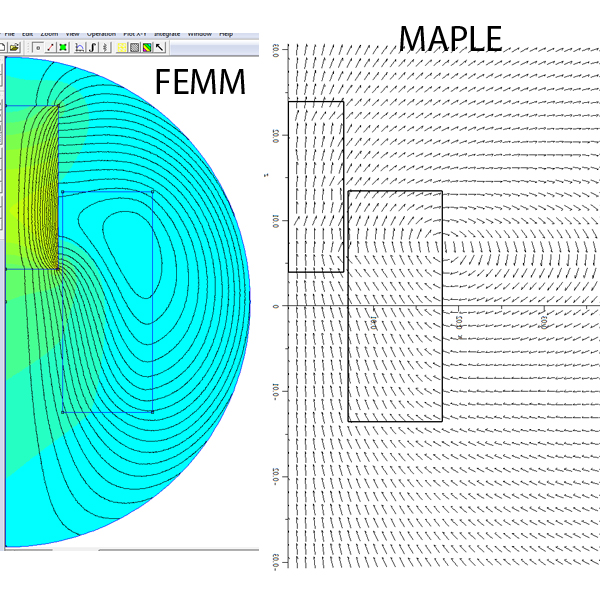


 J'ai finallement un graphique intermédiaire que je joint:
J'ai finallement un graphique intermédiaire que je joint: