Vitesse dans un mouvement circulaire uniforme

[romanouch]

Bonjour,

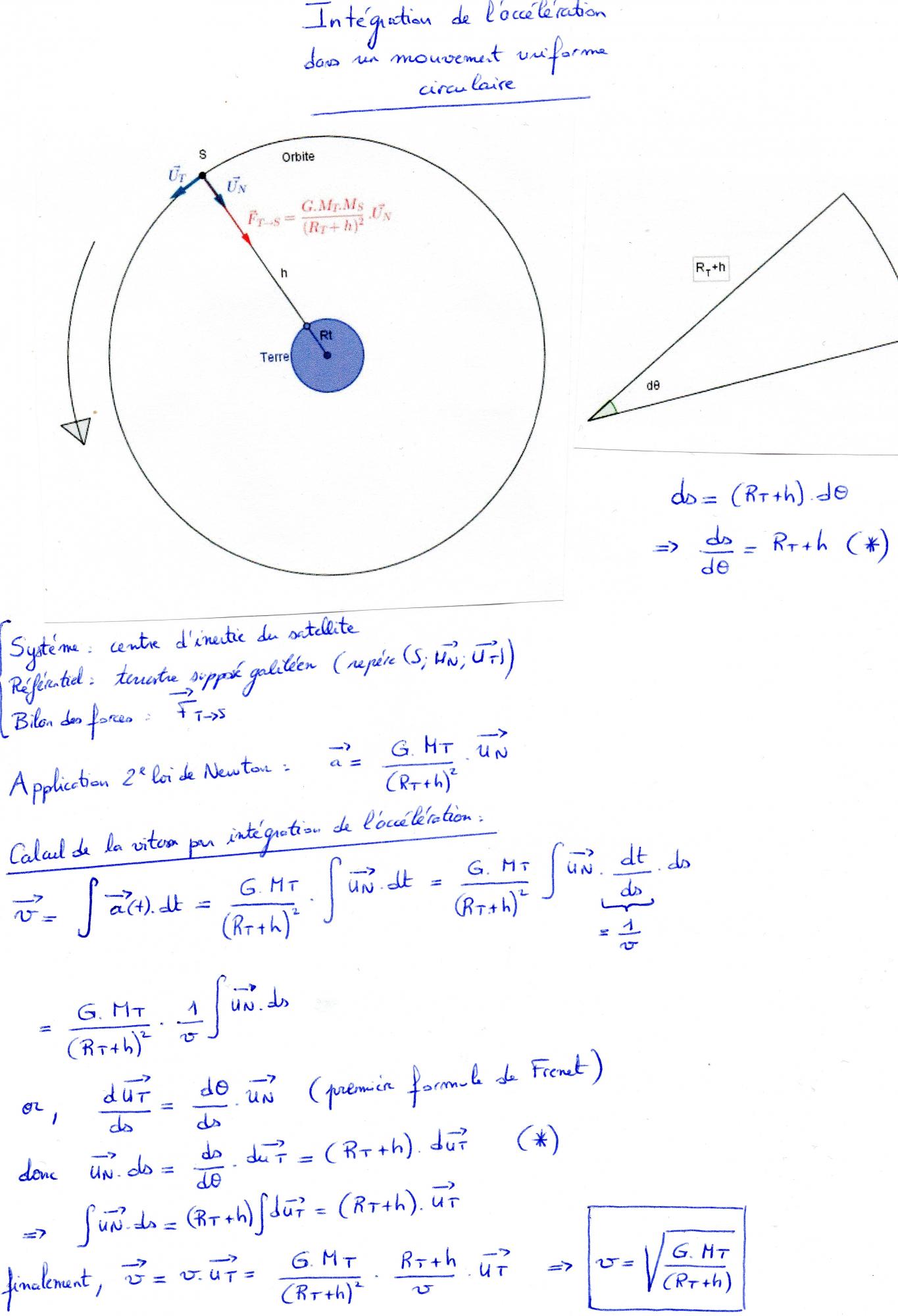
Je suis en train d'étudier le mouvement circulaire uniforme d'un satellite placé à une distance h de la Terre, soumis seulement à la force de gravitation.

Je n'ai pas de problème avec les démonstrations des expressions de l'accélération ou celle donnant . Je parle des démonstrations dérivation de vecteurs.

Je peux bien sûr obtenir l'expression de la vitesse en fonction de G, Rt, etc... en combinant les deux formules, mais je voudrais faire autrement.
Je voudrais partir de l'expression de l'accélération et en déduire l'expression de v. Et là, je bloque ou bien je tombe sur un résultat faux.

Comment intégrer l'accélération pour obtenir la vitesse?

D'avance merci.
-----

[PA5CAL]

Bonsoir

Il faudrait que tu donnes tes calculs qui aboutissent au résultat faux si tu veux qu'on t'aide à trouver la source de ton erreur (sinon, si c'est juste un copier-coller du cours qui t'intéresse, le forum n'est pas le lieu approprié).

[romanouch]

Bonjour,

Je pense avoir trouvé ma solution tout seul en refaisant le calcul. Merci quand même.

[romanouch]

Je scanne quand même mon calcul, est-il correct?

Je trouve le bon résultat, mais j'ai quand même une incompréhension: pourquoi lorsque j'intègre l'accélération, je ne rajoute pas v(0)?



Et dans ce cas, je ne vois pas comment terminer le calcul car je ne connais pas .

[A voir en vidéo sur Futura]

[interferences]

Bonjour,

C'est pas v(0) mais v(t_0) ou alors il faut changer l'indice à l'intégration.
Mais de toute façon, j'aime pas les intégrations vectorielles...trop compliqué.
Quelle composante de la vitesse de ton satellite tu connais parfaitement ?
Il faut que tu raisonnes sur celle là.

Au revoir

PS : j'ai pas encore vu la pièce jointe.

[PA5CAL]

Pour que le mouvement soit circulaire et uniforme, il faut nécessairement que la vitesse soit toujours perpendiculaire à l'accélération, avec un module constant dont la valeur dépend du rayon de la trajectoire et du module constant de l'accélération.

Donc, ceci étant imposé, ce qu'on ne connaît pas c'est seulement le plan dans lequel s'inscrit la trajectoire, et le sens dans lequel on tourne. Mais pour l'exercice je ne pense pas que cela ait de l'importance.

[interferences]

Re,

Si tu n'y arrive pas, petit exercice :

Position est accélération d'une particule :






Position est accélération d'une particule :





La différence dans ce cas c'est que le vecteur dépend du temps contrairement à et .
Il va falloir le dériver par rapport au temps.

Indices : et .

[romanouch]

Re,

Si tu n'y arrive pas, petit exercice :

Position est accélération d'une particule :






Position est accélération d'une particule :





La différence dans ce cas c'est que le vecteur dépend du temps contrairement à et .
Il va falloir le dériver par rapport au temps.

Indices : et (uv)'=u'v+uv'.

Bonsoir et merci de votre réponse,
Je n'ai pas de souci dans ce sens. En dérivant, par rapport au temps, par rapport à l'angle, et en utilisant les formules de Frenet. L'exercice proposé est exactement celui qu'il faut faire pour comprendre, je vous remercie d'avoir pris le temps de le taper.
Mais c'est vraiment l'intégration qui me pose souci, et notamment cette histoire de v(t0). Sans le considérer, je tombe sur le bon résultat. Pourtant, mathématiquement, j'aurais du le prendre en compte et il n'est pas nul. Pourquoi? Voilà ce que j'essaie de comprendre maintenant.

[QuarkTop]

Bonsoir et merci de votre réponse,
Je n'ai pas de souci dans ce sens. En dérivant, par rapport au temps, par rapport à l'angle, et en utilisant les formules de Frenet. L'exercice proposé est exactement celui qu'il faut faire pour comprendre, je vous remercie d'avoir pris le temps de le taper.
Mais c'est vraiment l'intégration qui me pose souci, et notamment cette histoire de v(t0). Sans le considérer, je tombe sur le bon résultat. Pourtant, mathématiquement, j'aurais du le prendre en compte et il n'est pas nul. Pourquoi? Voilà ce que j'essaie de comprendre maintenant.

Bonjour,
En fait on obtient ce qui marche aussi...

[romanouch]

Bonjour,
En fait on obtient ce qui marche aussi...

Bonsoir,

Pouvez-vous m'expliquer comment vous arrivez à ça?

[QuarkTop]

Bonsoir,

Pouvez-vous m'expliquer comment vous arrivez à ça?

Mettez tout simplement les bornes dans vos intégrales, comme tout à la fin de votre message #4 mais de manière cohérente (0 ou t0 partout mais pas les deux par exemple).

[romanouch]

Mettez tout simplement les bornes dans vos intégrales, comme tout à la fin de votre message #4 mais de manière cohérente (0 ou t0 partout mais pas les deux par exemple).

Bonjour,

J'avais une question mais maintenant j'en ai 3:
1. est-ce que mon calcul (ci-dessous) est correct?
2. Pourquoi dans mon changement de variable, les bornes de mon intégrale ne deviennent pas et et pourquoi la "fonction ne doit-elle pas devenir pour rester mathématiquement correct? (voir dans mon calcul en rouge)

3. Est-ce que dire que car est correct? (voir en vert)

Le calcul:

Je note:

Alors,

De plus, par changement de variable



Donc:

La base est orthonormale, on peut donc identifier les coefficients et obtenir le résultat suivant:



Si , alors

Donc

D'avance merci à ceux qui essaieront de m'aider.