Angle pour maximiser une accélération

[Olivier_B29]

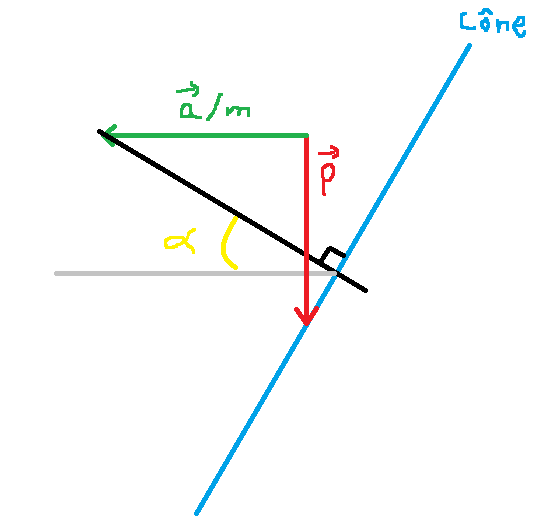
Bonjour, j'ai un problème de mécanique classique ou l'on cherche à déterminer l'angle optimal pour maximiser l'accélération, les forces étant constantes. Il s'agit de tirer un bloc sur un plan plat en présence de frottement. On cherche l'angle alpha entre la force qui tire et l'horizontale. En théorie pour avoir une accélération maximale selon l'horizontal (le bloc n'a pas de mouvement vertical) il faut que le cosinus soit maximal soit alpha=0 .
Mais un amis m'a parlé qu'il avait dérivé l'accélération et trouvait une valeur différente, proche de 0 degré mais différente.
Quelle est donc la bonne valeur à prendre en compte ?
-----

[LPFR]

Bonjour.
Eu lieu de parler d'accélération, ce qui ne fait que obscurcir le problème, il faut étudier la force horizontale de traction.
Faites un dessin.
Cette force est formée par la composante horizontale de la force appliquée, moins la force de frottement, laquelle dépend de la normale au sol, laquelle dépend du poids de l'objet et de la composante verticale de la force appliquée.
Exprimez donc, cette force horizontale résultante et calculez (en dérivant) la valeur le l'angle pour lequel elle est maximale.
Cela demande en tout lignes de calcul.
Au revoir.

[Olivier_B29]

J'ai déjà exprimer la force de traction précédemment pour la calculer. J'ai voulu calculer dF/d(alpha) et je me retrouve avec des cosinus et sinus que je ne peux simplifier pour isoler alpha. En dérivant l'accélération horizontale je trouve bien alpha=0.

[Calvert]

Salut !

et je me retrouve avec des cosinus et sinus que je ne peux simplifier pour isoler alpha. En dérivant l'accélération horizontale je trouve bien alpha=0.

C'est donc que tu as fait une erreur !

Une fois le dessin fait, comment sont exprimées les forces projetées sur les axes verticaux et horizontaux ?
(Je dois dire que je n'avais jamais vu ce problème auparavant, alors que c'est certainement un grand classique...)

[A voir en vidéo sur Futura]

[LPFR]

Re.
Donnez-nous l'expression que vous avez trouvée pour 'F'.
@Calvert: Oui. C'est un classique.
A+

[Olivier_B29]

Avec axe des x positif vers la droite et y vers le haut. Avec mes notations: Rn/uy ( réaction normale) : opposé au poids vers le haut; -P/uy; -Rt/ux ( réaction tangentielle ou frottements). Et la force F Fcos(alpha)/ux Fsin(alpha)/uy
J'ai F=us*m*g/(cos(a)+us sin(a)) avec us coefficient statique de frottement et a=alpha

[LPFR]

Re.
Votre expression est incorrecte.
Et quand on trouve un sinus ou cosinus au dénominateur (ou une expression qui peut le rendre nul) on s'alarme et on vérifie qu'on ne s'est pas planté.
A+

[Olivier_B29]

Alors là ça me pose une grosse colle ! Qu'on soit d'accord, c'est l'expression de F que j'ai donné et non sa dérivée. Pour info l'expression de F a été déterminée lors de la recherche de la force à appliquer pour mettre en mouvement l'objet. Même méthode qu'en TD, ici la dimension est bonne et la valeur trouvée est totalement plausible. À moins qu'une classe entière ce soit plantée dans l'exercice je ne comprend pas...

[interferences]

Bonjour,

Je ne connais pas cet exo, même si c'est un classique à priori.
Première chose, que je fais, je balance les équations par la fenêtre et je fait un dessin.
Je sais qu'il y a le poids, la réaction du sol portée par le cône de frottement et l'accélération horizontale.
AH...Une chose en plus, je sais que j'ai la distance la plus courte entre une droite est un point en traçant la perpendiculaire à celle-ci passant par le point.



Bon, j'ai un peu modifié le problème là en posant une accélération connue (toi je crois que tu as la force de connue) mais après c'est kifkif bourricot.
C'est juste un problème de géométrie.

[interferences]

PS : Je me demande, si je ne me suis pas planté, vu que ça me paraît un peu trop simple. Si LPFR a parlé de dérivation. Moi, je trouve l'angle du cône.
Bon, faut dire que j'ai fait quelques hypothèses du genre que ma force de traction s'exerce au centre de gravité.

[Olivier_B29]

Problème résolu en utilisant l'équation de l'accélération horizontale m*ax=F cos(a) - Rt en sachant qu'en mouvement Rt=us*Rn. On retrouve Rn avec l'expression de l'accélération verticale. On remplace dans l'expression en x, puis en dérivant je trouve bien un angle différent de 0, et bien vérifié par le calcul également, quand on prend a=0 l'accélération et légèrement plus faible.