Somme des forces

[invite86cd2fbf]

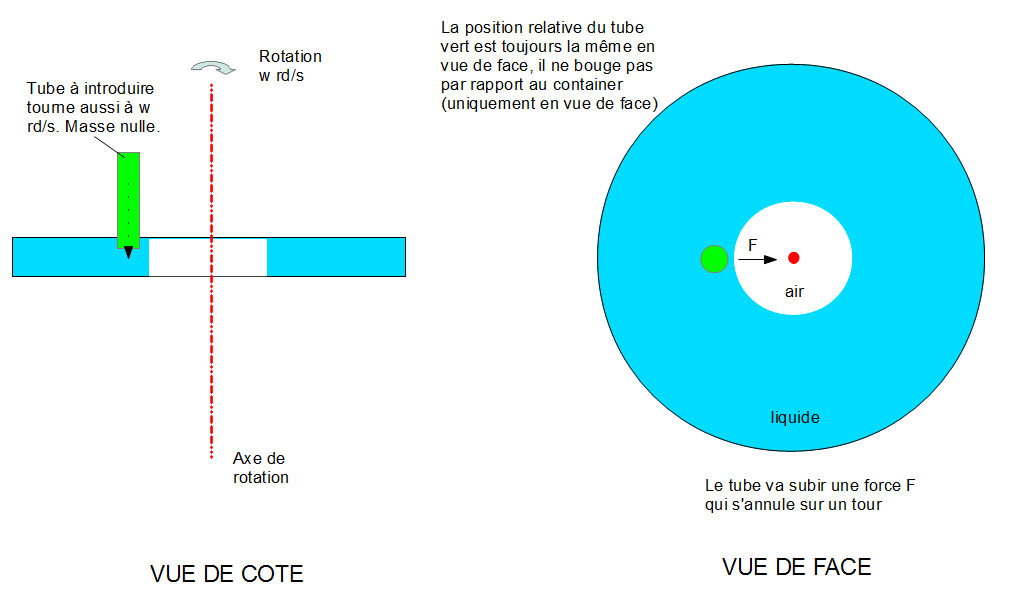
Bonsoir,

Un récipient circulaire (bleu) contient de l'eau, il tourne en rotation. L'axe de rotation est vertical, il passe par le centre du cercle formé par le récipient. Le volume du récipient est plus grand que le volume d'eau, du coup au centre il y a de l'air car l'eau est plaqué sur l'extérieur. Un tube de masse quasi nulle, parallèle à l'axe de rotation et maintenu par ce dernier est enfoncé rapidement dans l'eau. Le tube tourne à la même vitesse que l'eau. Le tube ne peut pas bouger une fois dans l'eau car l'axe le maintien. Comme le tube subit une force vers le centre à cause de l'eau, c'est qu'une partie de la parois reçoit une force additionnelle. Je ne trouve pas laquelle. Vous pouvez m'éclairer ? La force du tube s'annule sur un tour mais en attendant cela voudrait dire que le récipient bouge un peu tout seul, donc la paroi doit recevoir une force qui annule la force sur le tube. J'ai des difficultés à comprendre que les forces sur la paroi externe ne sont pas toutes les mêmes à cause de l'eau qui met la pression.



Merci d'avance de vos réponses
a++
-----

[f6bes]

Bjr à toi,
Si ton tube tourne , il reçoit une forçe centrifuge qui tend à le pousser vers l'extérieur et non vers le centre.
Je ne comprends pas ta phrase: "...le tube subit une force vers le centre.."
Bon WE

[invite86cd2fbf]

Bonjour,

La masse du tube est supposée nulle. Pour la phrase, "...le tube subit une force vers le centre..", l'eau n'a pas plus de pression avec le rayon grand ? la pression de l'eau n'est pas la même partout ? Donc je pensais que le tube subissait une force vers le centre, si ce n'est pas le cas, j'aimerai comprendre pourquoi la pression de l'eau est la même partout svp.

merci
a++

[calculair]

Bonjour,

Le tube a une masse nulle. La force centripète F = M W**2 R est nulle car M = 0

Quant à la force d'Archimède, l'accélération au point ou le tube est mis dans l'eau est ( W**2 R) ou R est la distance Tube /centre

la masse d'eau déplacé est d 3,14 r*2 h ou r est le rayon du tube et h la profondeur enfoncée dans l'eau et d la densité de l'eau. La poussée d'Archimede centripète est 3,14 r**2 h d W**2 R.

a cette poussée il faut ajouter la poussée d'Archimède verticale liée à g qui est 3,14 r**2 h d g

[A voir en vidéo sur Futura]

[invite86cd2fbf]

Re,

Merci pour la force de poussée ! Donc comme le tube est maintenu en radial par l'axe (mais le tube tourne à la même vitesse de rotation que l'eau) et que le centre de gravité de l'ensemble ne bouge pas, cela signifie que les forces sur la paroi externe du récipient n'est pas constance en chaque point ? Si j'imagine la couche externe, je comprends que la force de pression due à la mini "colonne" d'eau (un simple rayon) donne moins de force lorsqu'il y a le tube, d'un autre côté, les molécules sur les côtés d'une même couche devraient pousser les molécules "sous" le tube, non ? Je ne comprends pas pourquoi les molécules d'une même couche (rayon identique) ne donnerait pas la même pression.

a++

[invite86cd2fbf]

re,

j'ai compris, le centre de gravité de l'ensemble bouge,on passe de cg1 à cg2, donc la force de pression à gauche sur la paroi du récipient augmente car le rayon augmente. J'ai quand même une question sur la compensation des forces: le centre de gravité se calcule avec une loi linéaire, mais les forces dues à la pression sont fonction de r², c'est bien cela ?

a++

[calculair]

bonjour,

Les forces de pression dans le sens horizontal quand le disque tourne sont bien en R**2

Pour la force d'accélération en W**2 R
Pour la distance au centre e R

donc globalement en W**2 R**2

[invite86cd2fbf]

Bonjour,

D'accord, donc pour un rayon donné, la pression est bien constante ? Si je veux faire le calcul, je peux directement intégrer en prenant le rayon R comme paramètre de pression (W constant) ? Je vais prendre un objet plus simple.

Merci
a++

[invite86cd2fbf]

Bonjour,

J'ai une question d'ordre général sur un simple disque en rotation autour de son centre. Une demie partie solide et une demie partie liquide. Il y a les forces F entre le liquide et le solide. C'est donc pour compenser une force moindre que fournit la partie solide par rapport à la partie liquide mais je ne vois pas laquelle ? Si vous avez une explication ? Merci

a++