Pendule de Torsion - Exao

[invitec7021ce7]

Bonjour,

Je suis en train de préparer une manip de physique, qui me donne du fil à retordre, principalement sur le plan de la technique employée.
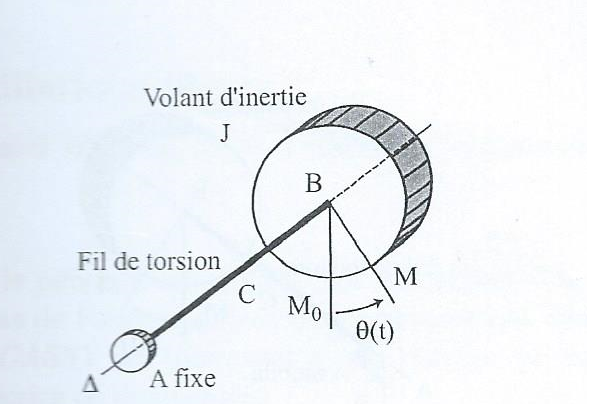
Ce pendule de Torsion est un peu différent de ce qu'on peut trouver sur le Net, puisqu'il est à masse simple.
En voici un petit schéma explicatif:



Nous disposons d'un logiciel pour mesurer l'angle de rotation, le capteur de déplacement est une roue ajourée dans ce cas.

L'équation du mouvement en oscillation libre est donnée par la relation suivante :



J: moment d'inertie du volant par rapport à l'axe delta
k: coefficient de proportionnalité du couple de freinage par rapport à la vitesse angulaire
C: constante de torsion du fil AB

Si on veut formaliser ça avec des coefficients physiques cela nous donne :



=
=



On peut facilement trouver C par une mise en équation du moment résultant lorsque le système est à l'équilibre. On peut également mesurer grâce à la courbe obtenue par =f(t).

Deux questions me taraudent :

Je ne comprend pas le principe de la mesure de l'angle à travers un tel dispositif.
De plus je m'interroge sur la façon dont on peut dégager J ainsi que l'amortissement à partir de ces seules informations. A priori je n'ai aucune donnée préalablesur la valeur de k.

Si quelqu'un a déjà rencontré ce genre de système auparavant ça me serait d'une très grande aide,


Cordialement,
-----

[LPFR]

Bonjour.
Je crois qu'il vous manque des informations.
La mesure de l'angle se fait en connaissant l'écartement angulaire entre les ouvertures. Pour il faut mesurer le moment où la lumière passe par une ouverture. C'est à dire que vous mesurez plutôt .
Mais pour avoir C il vous faut quelque chose qui permette de mesurer le couple.
Pour connaitre J il faut connaitre la période d'oscillation et (éventuellement) l'amortissement s'il est assez important pou modifier notablement la période.
Et pour connaitre l'amortissement il faut mesurer l'amplitude d'oscillation en fonction du temps.
Au revoir.

[invitec7021ce7]

En fait pour déterminer C, on nous invite à utiliser une masse afin de créer un couple de torsion qui produit une rotation que l'on peut mesurer à l'aide du logiciel.
La difficulté est ici d'imaginer une telle mise en place.
Par rapport à J, si j'ai bien compris on considère ici que à cause du fait que l'amortissement est négligeable devant
Sur une sinusoïde amortie, la valeur de sera donc donné par la valeur absolue de l’extremum à t=0, à la phase près.

Merci beaucoup pour votre réponse,

[LPFR]

Re.
Je déduis que le positionnement est comme dans le dessin. Et que quelque chose fait que ça tient. Par exemple que le fil de torsion est tendu horizontalement des deux côtés.
Dans ce cas vous pouvez accrocher une petite masse au cylindre, soit avec un fil soit collée. Ou, si le cylindre est magnétique, utiliser un petit aimant.
Si delta est faible vous ne pouvez le mesurer qu'a partir de la décroissance exponentielle de l'amplitude d'oscillation. Dont la constate de temps est précisément 1/delta (à vérifier).
A+

[A voir en vidéo sur Futura]

[stefjm]

De plus je m'interroge sur la façon dont on peut dégager J ainsi que l'amortissement à partir de ces seules informations. A priori je n'ai aucune donnée préalablesur la valeur de k.

Juste une remarque :
n'est pas un amortissement (sans dimension) mais un temps.

Pour que ce soit un amortissement, il faut écrire :