Bonjour à tous!
Peut-on traiter le cas d'une poutre hexagonale comme si c'est une poutre circulaire?
Sachant que la poutre est soumise à un couple de torsion et est encastré par sa base.
Voici un schéma:
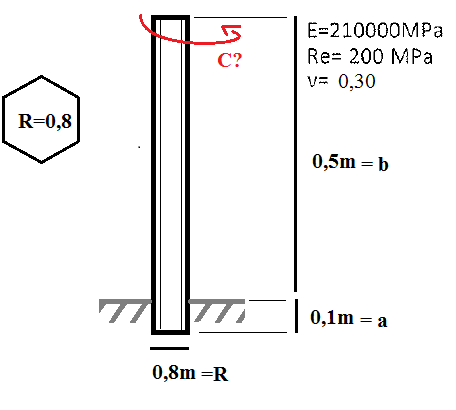
-----

Bonjour à tous!
Peut-on traiter le cas d'une poutre hexagonale comme si c'est une poutre circulaire?
Sachant que la poutre est soumise à un couple de torsion et est encastré par sa base.
Voici un schéma:



Bonjour.
C’est proche d’une poutre circulaire, mais pas égale.
Vous trouverez la formule dans Wikipedia :
http://fr.wikipedia.org/wiki/Barre_de_torsion
Au revoir.

B'jour,
On peut considérer une poutre circulaire à condition de prendre le diamètre du cercle inscrit pour rester sécuritaire.
Il y a aussi les formules toutes faites
tau = M / (0,217.A.d)
A aire de la section, d diamètre (inscrit).
theta = M / (0,133. G. A. d²)
Mais si t'as l'gosier, Qu'une armure d'acier, Matelasse. Brassens, Le bistrot.

La différence est uniquement dans le moment quadratique pour les déformations et le I/v pour les contraintes .
La valeur v est mesurée sur angles , pas sur plats .

Merci
Mais j'ai ça différemment, cela vous semble t-il correct?
Résolution:


Bonjour, Questionman,
Votre diamètre du cercle inscrit c'est 0.8 [m] ou 8 [mm].
Cordialement.
Jaunin__

0,58*200/1,3 = 89

Je te donne la formule pour l'hexagonal et tu prends celle pour une elliptique.
Mais si t'as l'gosier, Qu'une armure d'acier, Matelasse. Brassens, Le bistrot.

Non, ça ne marche pas quand la section n'est pas circulaire. La contrainte n'est pas proportionnelle à v de plus elle est maxi au milieu des plats.
Mais si t'as l'gosier, Qu'une armure d'acier, Matelasse. Brassens, Le bistrot.

Il faudrait savoir si c' est un exercice scolaire ou un calcul pour une application réelle .
Le coef de 1,3 , ça me parait très scolaire ...
Si j' avais eut à faire ça dans mon boulot , j' aurais pris le rayon moyen entre les plats et et le pointes , c' est suffisamment précis pour un besoin réel .

Ok, j'avais pas capté.Il y a aussi les formules toutes faites
tau = M / (0,217.A.d)
A aire de la section, d diamètre (inscrit).
theta = M / (0,133. G. A. d²)
C'est 8mm.Votre diamètre du cercle inscrit c'est 0.8 [m] ou 8 [mm].
Effectivement ça fait 89.0,58*200/1,3 = 89
Oula...
Quand la section est circulaire les contraintes sont max. en périphérie?Non, ça ne marche pas quand la section n'est pas circulaire. La contrainte n'est pas proportionnelle à v de plus elle est maxi au milieu des plats

8 mm , c' est un diamètre ou un rayon ?
Pour moi , R 8 c' est plutôt un rayon .

Diamètre = 8mm.

Une information :
http://www.formules-physique.com/categorie/299

Une autre information plus complète.
https://www.sendspace.com/file/gva0v5



bonjour s'il vous plait est ce qu'il y a quelqu'un qui peut m'aider dans le même probléme sauf que j'ai une poutre hexa soumise à la charge du vent j'aurai pas trouver le moment quadratique ?

