Disques en double rotation et somme des couples

[CZ48]

Bonjour,

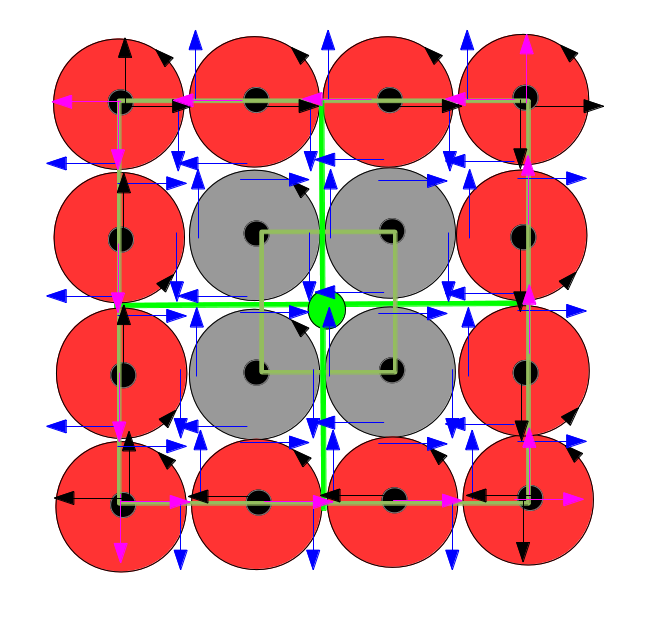
16 disques tournent ensemble à la vitesse w1 (sens horaire) autour de l'axe vert :

d2.png

Les disques rouges tournent autour de leur axe à la vitesse w2' (sens trigo) alors que les disques gris tournent autour de leur axe à la vitesse w2 (sens trigo), ce sont des vitesses relatives au disque

d1.png

Chaque disque est en contact avec son voisin et cela fournit une force F quelque soit la vitesse de rotation relative, car les frictions sont différentes:

d3.png

Avant t=0, on lance les disques à la vitesse w1,w2 et w2'. A t=0, on coupe le système qui permet d'entraîner les disques et on mesure les travaux des couples. Il n'y a pas d'autre friction que celle des disques. Le système est isolé.

On a : w1 > w2 et w2 > w2'

La mesure des couples est :


Disques: Frt(8(w1−w2)+24(w1−w2')+16(w1− w2))
Friction : +4Fr(w2+w2)t+16Fr(w2'+w2')t+8F r(w2+w2')t
Coins: -16Fw1t(3r)

La somme = 48Frtw1 -24Frtw2 - 24Frtw2' + 16Frtw2 + 40Frtw2' - 48Frtw1 = -8Frtw2 + 16Frtw2'

La somme est différente de 0, hors je pense que l'énergie doit être constante car le système est isolé et que je tiens en compte l'énergie calorifique. Donc, j'ai fait une erreur, si vous pouvez m'aider à trouver où SVP ?

Merci par avance pour votre aide
-----

[LPFR]

Bonjour.
Ce n’est vraiment pas clair. En particulier les frottements et les travaux.
Où est que vous tenez compte de l’énergie thermique ?

Détaillez le calcul des travaux. Et en particulier la façon d’écrire. Est-ce que Frt est F.r.t ou quelque chose d’autre.

Quand des disques frottent contre d’autres disques qui ne sont pas coaxiaux, le calcul des couples mérite d’être regardé de près. Ce couples peuvent ne pas être identiques (et de signe opposé), et le moment angulaire de disques peut se transformer en moment angulaire de l’ensemble de votre montage.

Essayez de commencer par un système avec le minimum de disques. Votre habitude de multiplier les disques et les sphères ne sert qu’à rendre plus opaque la situation.
Au revoir.

[CZ48]

Bonjour,

Je tiens compte de l'énergie thermique dans friction: +4Fr(w2+w2)t+16Fr(w2'+w2')t+8F r(w2+w2')t, et je pense que l'erreur viens de ce terme justement

Oui: Frt = F*r*t et 4Fr = 4*F*r

J'ai oublié de nommer:

r= rayon du disque
t= temps
F= force de base identique dès qu'il y a un contact


J'ai appliqué cette méthode pour un nombre moins important de disque, la couche intérieure uniquement, la couche extérieure uniquement et cela fonctionne, j'obtiens bien 0, mais c'est les deux couches ensemble qui me pose problème avec précisément (w2+w2'), je ne sais pas si j'ai le droit d'écrire cela ?

Quand des disques frottent contre d’autres disques qui ne sont pas coaxiaux, le calcul des couples mérite d’être regardé de près. Ce couples peuvent ne pas être identiques (et de signe opposé), et le moment angulaire de disques peut se transformer en moment angulaire de l’ensemble de votre montage.

je ne comprends pas tout, je pensais que mon calcul était clair

a+

[CZ48]

Je viens de comprendre votre message et oui effectivement certaines forces font appliquer un couple aux disques: Frt(8(w1−w2)+24(w1−w2')+16(w1− w2)) et d'autres forces s'appliquent sur le montage: -16Fw1t(3r). J'ai d'ailleurs bien une compensation avec les termes en w1.

Ensuite, j'ai écrit "somme des couples" mais c'est la somme des travaux des couples que je regarde, j'ai écrit un peu vite. Les 3 calculs sont les travaux des couples et c'est pour cela que la somme doit être nulle car le système est isolé.

a+

[A voir en vidéo sur Futura]

[CZ48]

Re,

J'ai fait une erreur, j'ai fait un dessin avec toutes les forces et cela donne:



Les flèches bleues représentent les friction des disques, les flèches noires les forces venant de l'axe du disque et les flèches magenta sont les forces qui sont sur le support directement.

La mesure de la somme des travaux des couples est :


Travaux des rotations des disques: Frt(16(w1−w2)+32(w1−w2'))
Friction : +4Fr(w2+w2)t+12Fr(w2'+w2')t+8F r(w2+w2')t
Coins: -16Fw1t(3r)

La somme vaut bien 0.

[LPFR]

Re.
On peut prévoir ce qui va se passer.
Le frottement entre les disques fera qu’ils s’arrêteront de tourner les uns par rapport aux autres mais que l’ensemble se mettra à tourner de sorte que le moment angulaire global sera conservé.
L’énergie transformée en chaleur sera l’énergie initiale (somme des ½J.ω) moins l’énergie finale (même chose avec le bon moment d’inertie et la bonne vitesse de rotation).

Je n’ai pas vérifié votre formule. Dans le meilleur des cas, votre calcul du travail n’est bon que pendant el court instant où les vitesses angulaires sont celles que vous avez écrites. Mais toutes ces vitesses sont en train de diminuer. Donc, la puissance change tout le temps et le travail sera l’intégrale de cette puissance pendant que les vitesses relatives sont différentes de zéro.
A+

[CZ48]

Merci pour vos réponses. Est ce que je peux vraiment considérer que la formule est valable sur un delta 't', je veux dire sur le plan physique et mathématique, est ce une bonne méthode pour calculer la somme de l'énergie du système ? Si 't' est aussi petit qu'on veut alors ce genre de méthode permet de vérifier qu'on a bien 0 ?

a+

[LPFR]

Re.
Je ne peux pas vous dire.
Je ne comprends pas votre calcul.
A+

[CZ48]

J'ai calculer les travaux des rotations des disques (sur eux memes) dus aux couples, flèches bleues: 8 couples*2r pour la couche centrale = 16 puis 8 couples *2 + 8 couples *1 + 8 couples *1 pour la couche externe: Frt(16(w1−w2)+32(w1−w2'))
Le travail de la friction, flèches noires : +4Fr(w2+w2)t+12Fr(w2'+w2')t+8F r(w2+w2')t
Le travail des forces sur le support, flèches magenta: -16Fw1t(3r)

je sais pas si c'est assez clair, j'ai repris les flèches du dessin précédent.

a+

[LPFR]

Bonjour.
Au lieu de balancer de formules globales, donnez le calcul pour le travail dû au frottement entre deux disques. Peut-être que je comprendrai ce que vous avez fait.
Au revoir.

[CZ48]

Bonjour,

désolé, pour moi le travail résultant de 2 disques se frottant est de F*r*(wx+wy)*t avec wx et wy les 2 vitesses des disques, je ne sais pas si c'est juste.

cdlm

[LPFR]

Bonjour,

désolé, pour moi le travail résultant de 2 disques se frottant est de F*r*(wx+wy)*t avec wx et wy les 2 vitesses des disques, je ne sais pas si c'est juste.

cdlm

Re.
Bon. Nous sommes d’accord.
Alors comment vous arrivez à
Frt(16(w1−w2)+32(w1−w2')) ?
(Ce n’est pas le ‘16’ ni le ’32’ qui m’intriguent)
Qui sont w2 et w2’ ?
A+

[CZ48]

Ce sont les travaux des flèches bleues sur chaque disque, des couples travaillent selon moi à w1-w2 et à w1-w2' car w1 > w2 > w2' là non plus je ne sais pas si c'est correct. J'ai pris les flèches bleues deux par deux (avec parfois les flèches noires) pour avoir un couple sur chaque disque et je me suis dis que ce couple travaille sur w1 réduit de wx.

w2 = vitesse des disques couche intérieur
w2' = idem couche externe

a+

[LPFR]

Re.
Ceci n’est vrai que pour des disques coaxiaux.
Dans ce cas je ne vois pas le rapport avec le dessin du post #5.
A+

[CZ48]

Je dois me tromper. C'est pas grave.

Merci pour votre aide