Bonsoir,
Voilà j'ai un devoir de physique et j'ai un eu de mal avec cet exercice....
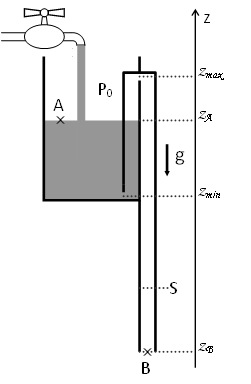
Le vase de Tantale
Le schéma ci-contre est celui d’un vase de Tantale. Il s’agit d’un récipient muni d’un siphon et alimenté par un robinet dont le débit constant est Q0. Le siphon, de section droite S, plonge jusqu’au fond du vase à une altitude zmin et remonte jusqu’à l’altitude zmax. Cette section S est prise beaucoup plus petite que la section du récipient. On note A un point de la surface et B un point situé à l’extrémité inférieure du siphon. Leurs altitudes respectives sont notées zA et zB. Notons que zA varie lorsque le vase se remplit ou se vide.
1. Que se passe-t-il lorsque le niveau de l’eau dans le vase (situé à l’altitude zA) atteint zmax ?
2. Dans certaines conditions que l’on considère pour l’instant remplies, on observe un phénomène cyclique de vidange et de remplissage du vase. Décrivez qualitativement un de ces cycles.
3. En appliquant la relation de Bernoulli entre les points A et B à un instant de la phase de vidange, établissez une relation entre les vitesses et les altitudes de ces points. Précisez les hypothèses qui autorisent cette application.
4. On peut ici négliger vA par rapport à vB. Pourriez-vous le justifier ? Exprimer alors le débit de la vidange QV pour une altitude zA donnée. A quel moment ce débit est-il minimal ? En déduire la condition pour observer le phénomène cyclique.
5. Calculez la pression minimale, pendant la vidange, au point le plus haut du siphon. Pourrait-on réaliser un vase de Tantale arbitrairement haut ?
Données :
- densité de l’eau : deau = 1
- densité du mercure : dHg = 13,7
- densité de l’air : d = 1,3 10-3
- constante de gravité : g = 9,81 m s-2
- pression atmosphérique = 105 Pa
1) Lorsque za=z(max) le siphon commence à se remplir.
2) 1. A t=o, Za=Zmin
2. t0<t<t1 : le vase de rempli
3. t=t1, Za=Zmax, le siphon se rempli
4. t1<t<t2, le vase est vidé par le siphon. Za diminue
5. Za=Zmin, le niveau du siphon est au niveau de Zmin
Et le cycle recommence.
3) Ici il faut juste écrire l'équation de Bernouilli : pa+1/2*rho*Va²+rho*gZa=pb+1/2*rho*Vb²+rho*gZb et donner les conditions nécessaires (pas de frottement, c'est un fluide parfait etc)
4) On utilise les sections pour expliquer pourquoi on peut négliger Va par rapport à Vb, donc on obtient : pa+rho*gZa=pb+1/2*rho*(Qv*t)²+rho*gZb
donc Qv=racine(2*(Pa-Pb+rho*g(Za-Zb))/rho) * 1/t
Le debit est minimal quand Za=Zmin (est-ce que je dois le démontrer avec la formule ??)
Qv>Qo sinon le fluide de va pas dans le siphon. (là aussi il faudrait une démonstration ?)
5) On cherche à calculer pb mais je ne comprend pas vraimet comment, puisqu'on a pas de données pour Qv ou t. Et Qv ne peut pas être négligeable pendant la vidange.
Est-ce qu'il ne faudrait pas plutôt utiliser deltaP=rho*g(ha-hb) ?
En tout cas merci beaucoup si vous pouvez m'aider !
-----