Mécanique des fluides (ballon dans l'eau, vase de tantale
Salut à tous !
Alors voilà, j'ai un DM de mécanique des fluides à faire et je suis un peu bloquée à certains points des exercices. Il y en a deux, donc, un sur un ballon de foot dans l'eau et un autre sur le système du vase de tantale.
Exercice 1 : Coule-t-il ?
Un ballon de football possède un rayon de 11 cm, pèse environ 500 g et est gonflé avec une surpression d’environ 0.8 bar par rapport à la pression atmosphérique. Si l’on tente de l’immerger dans l’eau, on ressent l’action de la poussée d’Archimède qui tend à le ramener à la surface mais que se passerait-il en grande profondeur ?
1. Calculez la force qu’il faut exercer sur le ballon pour le maintenir juste sous la surface de l’eau.
2. Comment évolue cette force lorsque l’on augmente la profondeur à laquelle le ballon est immergé ? A partir de quelle profondeur observe-t-on un changement ?
3. A quelle profondeur n’est-il plus nécessaire d’exercer de force pour le maintenir sous l’eau ? On considère l’air contenu dans le ballon comme un gaz parfait et on néglige les variations de température. Que se passe-t-il au delà de cette profondeur ? Concluez sur la probabilité qu’une telle expérience ait déjà été réalisée ?
Données :
- Constante de gravité terrestre : g = 9,81 m s-2
- Volume d’une sphère de rayon r : V = (4/3)r3
- Constante des gaz parfaits : R = 8,314 J mol –1 K-1
Pour cet exercice-là, je suis bloquée parce que je trouve mes résultats absolument incohérents :
1) Pour cette question j'ai fait la différence entre la poussé d'archimède et le poids du ballon. J'ai donc trouvé : 1000*5,58*10^-3*9,81-500*10^-3*9,81 = 52,83N. Je trouve ce résultat un peu grand mais pourquoi pas.
2) C'est là que ça se complique. Parce que la poussé d'archimède c'est bien une force de pression mais constante, non ? Mais est-ce qu'on a que le poids et la poussée d'archimède ou aussi une troisième force qui serait la pression de l'eau sur la balle ? (je vais peut-être chercher trop loin, je ne sais pas ...)
Avec seulement archimède et le poids, je trouve que la pression nécessaire est seulement de 32,25 Pa, mais c'est excessivement faible. (P=archimède/Surface du ballon)
Si on rajoute une autre force de pression à l'équation, je trouve 328Pa, mais ça n'est pas vraiment mieux ...
3) Du coup ici il faut utiliser la formule deltaP=rho*g*(hb-ha). Et donc je trouve soit 3,3mm, soit 33mm. Mais c'est impossible, c'est là que ça ne colle plus !
Après, je n'ai pas vraiment compris comment résoudre le reste de la question. Je suppose qu'il faut utiliser PV=nRT. Mais on chercherait à calculer le volume, ça serait un peu bizarre, non ?
Exercice 2 : Le vase de Tantale
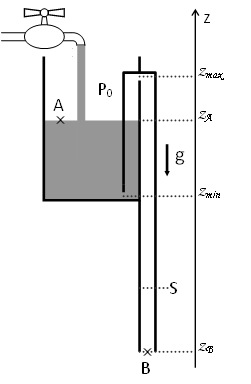
Le schéma ci-contre est celui d’un vase de Tantale. Il s’agit d’un récipient muni d’un siphon et alimenté par un robinet dont le débit constant est Q0. Le siphon, de section droite S, plonge jusqu’au fond du vase à une altitude zmin et remonte jusqu’à l’altitude zmax. Cette section S est prise beaucoup plus petite que la section du récipient. On note A un point de la surface et B un point situé à l’extrémité inférieure du siphon. Leurs altitudes respectives sont notées zA et zB. Notons que zA varie lorsque le vase se remplit ou se vide.
1. Que se passe-t-il lorsque le niveau de l’eau dans le vase (situé à l’altitude zA) atteint zmax ?
2. Dans certaines conditions que l’on considère pour l’instant remplies, on observe un phénomène cyclique de vidange et de remplissage du vase. Décrivez qualitativement un de ces cycles.
3. En appliquant la relation de Bernoulli entre les points A et B à un instant de la phase de vidange, établissez une relation entre les vitesses et les altitudes de ces points. Précisez les hypothèses qui autorisent cette application.
4. On peut ici négliger vA par rapport à vB. Pourriez-vous le justifier ? Exprimer alors le débit de la vidange QV pour une altitude zA donnée. A quel moment ce débit est-il minimal ? En déduire la condition pour observer le phénomène cyclique.
5. Calculez la pression minimale, pendant la vidange, au point le plus haut du siphon. Pourrait-on réaliser un vase de Tantale arbitrairement haut ?
Données :
- densité de l’eau : deau = 1
- densité du mercure : dHg = 13,7
- densité de l’air : d = 1,3 10-3
- constante de gravité : g = 9,81 m s-2
- pression atmosphérique = 105 Pa
J'ai eu nettement moins de difficulté pour cet exercice.
1) Lorsque za=z(max) le siphon commence à se remplir.
2) 1. A t=o, Za=Zmin
2. t0<t<t1 : le vase de rempli
3. t=t1, Za=Zmax, le siphon se rempli
4. t1<t<t2, le vase est vidé par le siphon. Za diminue
5. Za=Zmin, le niveau du siphon est au niveau de Zmin
Et le cycle recommence.
3) Ici il faut juste écrire l'équation de Bernouilli : pa+1/2*rho*Va²+rho*gZa=pb+1/2*rho*Vb²+rho*gZb et donner les conditions nécessaires (pas de frottement, c'est un fluide parfait etc)
4) On utilise les sections pour expliquer pourquoi on peut négliger Va par rapport à Vb, donc on obtient : pa+rho*gZa=pb+1/2*rho*(Qv*t)²+rho*gZb
donc Qv=racine(2*(Pa-Pb+rho*g(Za-Zb))/rho) * 1/t
Le debit est minimal quand Za=Zmin (est-ce que je dois le démontrer avec la formule ??)
Qv>Qo sinon le fluide de va pas dans le siphon. (là aussi il faudrait une démonstration ?)
5) On cherche à calculer pb mais je ne comprend pas vraimet comment, puisqu'on a pas de données pour Qv ou t. Et Qv ne peut pas être négligeable pendant la vidange.
Est-ce qu'il ne faudrait pas plutôt utiliser deltaP=rho*g(ha-hb) ?
Voilà, je sais que mon message est un peu long, mais ça serait génial si vous pouviez m'aider, surtout pour le premier exercicie parce que je suis vraiment bloquée et que je ne vois pas d'autres solutions pour le résoudre ....
Merci !! ^^
-----
Envoyé par LPFR 
). Donc on a un volume qui diminue, comme la poussée d'archimède jusqu'à ce que celle-ci soit égale au poids. En fait on veut la pression à laquelle elle est égale à 4,905N, si j'ai bien compris. Mais je ne vois toujours pas comment trouver la pression ... on ne peut pas utiliser PV=nRT puisque le volume varie et qu'on ne le connait pas, non ? Si le volume varie, la surface aussi.... alors comment peut-on calculer une pression ? 
