Physique électromagnétisme

[alex98125]

Bonjour,

Quelqu’un peut m'aider dans cet exercices à trouver la quantité d'électricité qui se déplace à travers la boucle, je n 'arrive pas à obtenir la valeur 2,64 C

Merci,

-----

[alex98125]

j'ai calculer "R= Pl/s" et "Phi=B S cos", mais en faisant "q= - Phi/R", je n'obtient pas 2,64 C

[LPFR]

Bonjour et bienvenu au forum..
Je trouve que l’énoncé c’est du n’importe quoi.
D’abord le champ produit par une spire n’est pas constant et dépend de la position radiale (et axiale).
Pour passer d’une valeur non nulle à une valeur nulle il suffit que le courant s’interrompe.
On ne peut pas le faire instantanément à cause de l’inductance. Mais on peut le faire aussi vite que l’on veut.
Donc, on n’a pas besoin de faire circuler de la charge (ou presque rien) pour faire chuter le champ à zéro.

Dans quelle poubelle avez-vous trouvé cet exercice ?
Au revoir.

[Resartus]

Si je comprends bien les formules, l est la circonference de la boucle, s la surface du fil de cuivre, et p est en fait un rho (résistivité du cuivre), La formule de la résistance semble donc correcte.
Par contre, dans la deuxième formule, je ne comprends pas le "cos" (où alors il doit être égal à 1 dans cette configuration?)
OK pour la troisième

La valeur de rho du cuivre est-elle fournie? sinon quelle valeur avez-vous utilisée? Et pouvez-vous nous présenter votre calcul pour voir où il y a une erreur?

[A voir en vidéo sur Futura]

[LPFR]

...
OK pour la troisième
...

Re.
Je ne connais pas cette formule.
D’où vient-elle ?
A+

[alex98125]

J'ai essayer plein de calcul mais je n'arrive pas a obtenir 2,64 C, et voici la version qui pour moi semble la plus logique:

[Resartus]

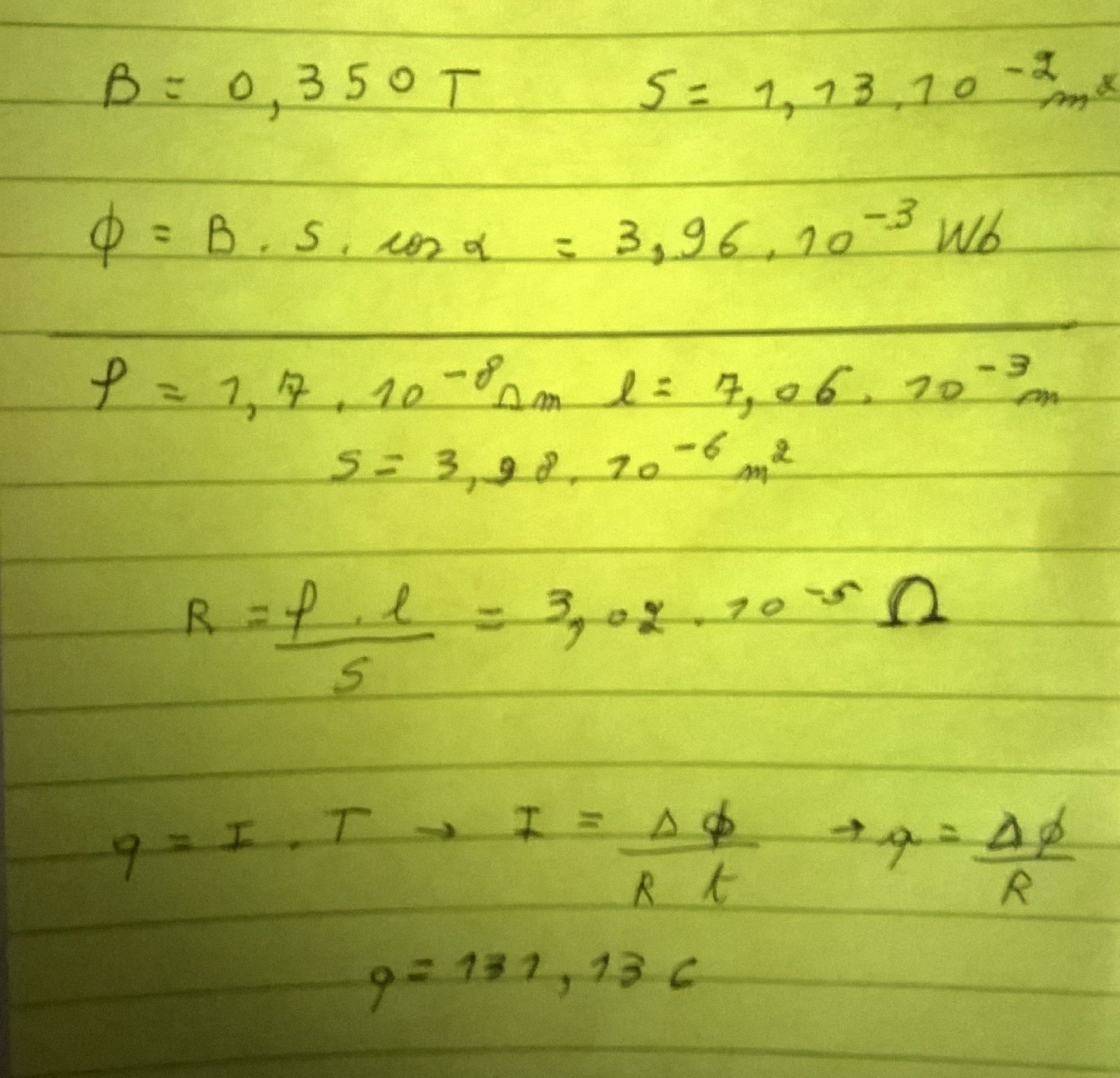
LPFR :
L'exercice demande l'action de la variation d'un champ sur un conducteur. Il apparait dans la spire une force contreelectromotrice égale à dphi/dt, qui se traduit si la boucle a une résistance R par un courant instantané i=dphi/dt/R. Quand on intègre, cela donne la circulation d'une charge totale égale q= Deltaphi/r

[Resartus]

Erreur sur la longueur de la boucle. l vaut pi*0,12

[LPFR]

LPFR :
L'exercice demande l'action de la variation d'un champ sur un conducteur. Il apparait dans la spire une force contreelectromotrice égale à dphi/dt, qui se traduit si la boucle a une résistance R par un courant instantané i=dphi/dt/R. Quand on intègre, cela donne la circulation d'une charge totale égale q= Deltaphi/r

Re.
J’ai compris. Merci. La spire est en court-circuit et se trouve dans un champ magnétique « externe » qu’on diminue.
J’avais interprété que le champ était celui produit par la spire elle-même.
A+