Courroie surfacique

[xt63]

Bonjour,

Je souhaite savoir s'il est possible d'avoir deux poulies de rayons différents reliées par une courroie et avoir la même vitesse angulaire ?

Pour cela, j'ai imaginé la possibilité, théorique bien entendu, d'avoir une poulie surfacique, il n'y a rien à l'intérieur (en théorie). La poulie1 a un rayon 2R, la poulie2 a un rayon R. Lorsque la courroie passe de la poulie1 à la poulie2, j'augmente la section de la courroie. Si au départ la courroie fait s1=2mm * 2 mm de section en passant à la poulie2 je pense qu'il faudrait avoir une section de s2=2mm*6mm pour garder la même surface de matériau. Pour le calcul, j'ai pris pour la courroie qui vient de la poulie1 comme 4 surfaces à 2*2 soit 16 mais comme le rayon est de 2 il y aura 32. Pour la poulie2, j'ai augmenter la section en rectangle donc 2 faces restent de même largeur, donc cela donne 2 surfaces à 2*2 et 2 surfaces à 6*2 soit 8+24=32.

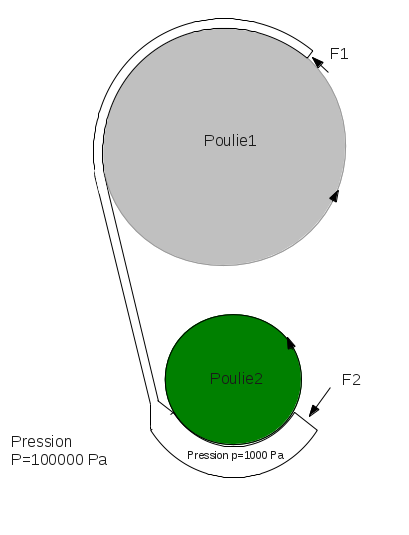
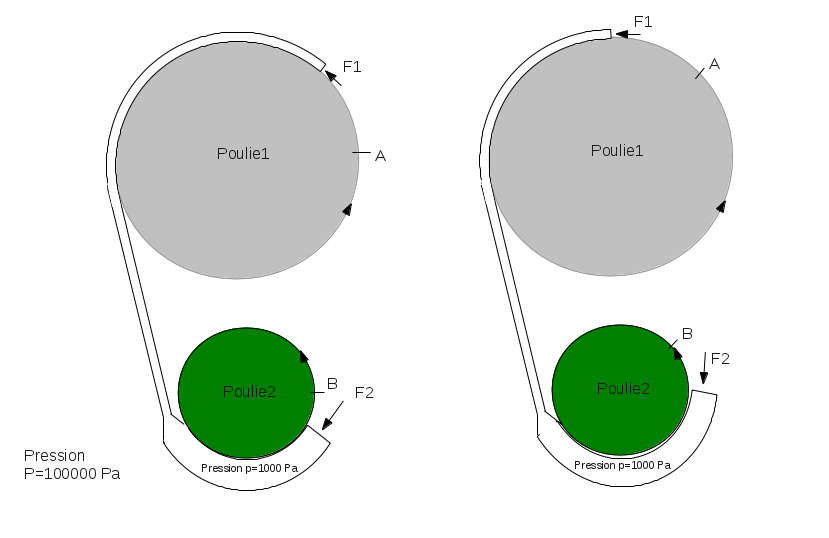
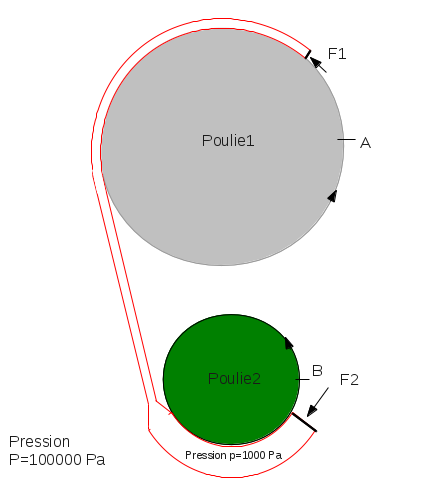
Voici le dessin:



Une poulie transmet un couple vers une autre poulie, il est possible de le faire en utilisant par exemple la pression d'un gaz: à la place de la courroie, je prends un tuyau, il est enroulé en partie sur la poulie1 et en partie sur la poulie2. A l'extérieur, il y a la pression de l'atmosphère P=100000 Pa et à l'intérieur du tuyau il y a une pression 100 fois plus faible, p=1000 Pa. Le tuyau est fermé. La poulie1 va recevoir le couple s1*(P-p)*2R, la poulie2 va recevoir le couple -s2*(P-p)*R. La poulie1 subit la force F1 et la poulie2 subit la force F2, comme la surface du tuyau avance perpendiculairement à la force de pression cela ne demande pas d'énergie. La poulie2 perds plus d'énergie que la poulie1 mais j'augmente le volume du tuyau, il passe de s1*L à s2*L donc il augmente de (s2-s1)*L et j'ai bien la somme de l'énergie constante. Le raisonnement est-il correct ?

Merci par avance.

Bien cordialement
-----

[coussin]

J'ai rien capté...
Les poulies, ça marche par un principe de non-glissement (encore plus évident avec une chaîne de vélo). Rien à voir avec des pressions...

[xt63]

Bonjour,

J'ai peut être été vite en explication. Je souhaite savoir si je peux avoir 2 poulies de rayons différents reliées par "quelque chose" tout en ayant la même vitesse angulaire. Si j'utilise une courroie avec friction ça ne fonctionne pas, donc j'ai pensé à autre chose: un tuyau et une différence de pression. La poulie2 pourrait être celle qui fournit de l'énergie, la poulie1 celle qui reçoit et le tuyau dans le cas présent augmente son volume, j'ai pas trouvé ce qui permettrait de transmettre 100% de l'énergie entre la poulie1 et la poulie2, mais il y a peut être autre chose si vous savez ?

Je souhaite savoir si mon raisonnement est correct:

1/ La surface totale du tuyau doit rester la même
2/ déplacer le tuyau ne demande aucune énergie en théorie car la force provenant de la pression est perpendiculaire au déplacement sauf là où il y a F1 et F2 (bouts du tuyau)
3/ comme les 2 poulies tournent à la même vitesse cela signifie que pour garder constant la surface, je passe d'une section 4 à une section de 12
4/ si les sections sont correctes cela veut dire que le volume du tuyau passe de V à 1.5V, car le rayon de la poulie1 est 2R et non R

Dans mes calculs j'ai bien la somme de l'énergie constante, donc j'imagine que c'est correct, je veux juste avoir une confirmation.

Cordialement

[obi76]

Bonjour,

idem, absolument rien compris. Ce serait la viscosité du gaz qui entrainerai l'une des deux poulies, gaz qui a été mis en mouvement par la première ?

[A voir en vidéo sur Futura]

[xt63]

Re,

Non, c'est la différence de pression entre l'intérieur du tuyau et l'extérieur qui donne un couple sur chaque poulie (là où se trouvent les forces F1 et F2). A l'extérieur il y a 100000 Pa et à l'intérieur du tuyau il y a 1000 Pa. Dans mon exemple, je veux faire tourner les poulies dans le sens trigo donc il faut qu'une poulie soit montée sur un moteur (la poulie2) car le couple provenant de F2 la freine et une poulie (la poulie1) sera montée sur l'objet à faire tourner et qui recevra un couple provenant de la force F1. Le moteur monté sur la poulie2 doit donner de l'énergie pour contrer le couple provenant de la force F2, et cela permet d'entraîner la poulie1 et d'augmenter le volume du tuyau qui augmente car il faut bien laisser la surface du tuyau constante (pas de perte de matière). J'ai essayé de trouver un autre moyen pour que la poulie2 donne 100% à la poulie1 mais je n'ai pas trouvé, peut être que ça existe.

Un courroie standard est passive, une poulie la tire et la courroie tire donc l'autre poulie. Ici, comme je veux avoir les deux vitesses angulaires identiques, je dois trouver un moyen me permettant de conserver cette vitesse angulaire alors que les rayons ne sont pas identiques mais il faut aussi que la poulie transmettent le couple, j'utilise donc une différence de pression (le tuyau est actif finalement) pour avoir les forces F1 et F2 sur chaque poulie car si je transmet le couple directement ça marche pas. Les forces F1 et F2 me donnent deux couples, un positif et un négatif, et le couple où la demande d'énergie est la plus importante est sur la poulie2 donc le moteur doit être sur la poulie2 et le récepteur sur la poulie1. Voilà j'espère que c'est un peu plus clair, c'est un fonctionnement bizarre je vous l'accorde. J'aimerai savoir si mon raisonnement de ce fonctionnement est correct et sur les calculs pour la surface et le bilan énergétique.

Cordialement

[coussin]

Votre courroie est fermée. Il n'y a pas de forces F1 et F2. Ce n'est pas difficile de voir que votre système est statique, rien ne bouge...

[xt63]

Ca dépend de ce que vous entendez par fermée, la courroie ne fait pas le tour complet pour se refermer sur elle même comme le fait une courroie standard (voir le dessin). Voyez cela comme un tuyau enroulé en partie sur la poulie1 et enroulé en partie sur la poulie2. Bien entendu comme il y a une pression différente dans le tuyau, il est fermé là où se trouve F1 et là où se trouve F2.

Cordialement

[xt63]

J'ai fait un dessin avec 2 positions en montrant deux points A et B fixe sur chaque poulie:



C'est la surface du tuyau qui se déplace perpendiculairement à la force de pression excepté là où se trouve F1 et F2 qui permettent d'avoir le couple sur chaque poulie.

Cordialement

[obi76]

Heu non, toujours pas compris.

La pression qui s'exerce sur chaque morceau de poulie fournira un moment nul, puisque chaque force élémentaire passe par le centre de chaque poulie...

[coussin]

Pis c'est une courroie magique pour rester collée aux poulies (si elle est ouverte)

[obi76]

Ca pue le mouvement perpétuel ce machin...

[obi76]

Ha ok, je pense avoir compris.

La vitesse de rotation de chaque poulie est imposée et égale, on met une courroie élastique (donc dont la section va augmenter entre la poulie 1 et la poulie 2 et diminuer dans l'autre sens), et le but est de savoir si on peut récupérer un travail avec la fluctuation de pression du gaz se trouvant dans la courroie.

J'ai bon ?

[xt63]

Hep, c'est pas un mouvement perpétuel, j'ai bien une énergie constante hein, j'ai fait les calculs. Je demande juste de vérifier svp.

La vitesse de rotation de la poulie2 est imposée par un moteur qui va donner de l'énergie. La poulie1 récupère une partie de l'énergie (elle va la donner à un récepteur) et l'augmentation du tuyau l'autre partie. Je donne 100 je récupère 100 si pas de friction (théorie). Je suppose que les poulies maintiennent le tuyau pour pas qu'il s'en aille bien entendu (j'ai pas dessiné tous les détails).

Par contre Obi76, la vitesse angulaire de rotation de la poulie1 devrait être la conséquence de la vitesse de rotation de la poulie2 et du fait qu'on fait avancer les parois du tuyau comme il faut (il faut imaginer un dispositif qui fait avancer les parois du tuyau comme j'ai envie), la poulie1 ne peut pas aller plus vite car le tuyau n'avance pas plus vite. Dans la chaîne de transmission, c'est poulie2->tuyau->poulie1. Et effectivement il y a un travail de la part du volume du tuyau qui augmente, le tuyau gagne en énergie potentielle sinon j'ai pas 100 au final mais moins.

J'espère que vous avez compris.

Cordialement

[obi76]

Ben pas trop. Si vous n'imposez pas la vitesse des poulies, alors la tension sur le tuyau sera constant partout, et donc son diamètre aussi...

[xt63]

La vitesse angulaire de la poulie2 est imposée. Quelque chose d'externe impose au tuyau de passer du diamètre1 au diamètre2, une sorte de gabarit qui force les parois à être comme je l'ai dessiné, la paroi suit ce gabarit (sans frottement). Et par conséquent la poulie1 tourne selon le couple grâce à F1. Mais effectivement il doit y avoir un asservissement nécessaire pour permettre à la poulie1 de ne pas écraser le tuyau peut être. C'est juste théorique mais est ce que vous comprenez mieux ?

Le bout du tuyau où se trouve F2 est fixé sur la poulie2 et le bout de tuyau où se trouve F1est fixé sur la poulie1. Le reste du tuyau qui passe dans le gabarit a une force perpendiculaire au déplacement.

Cordialement

[obi76]

Désolé, mais pour être honnête... encore moins...

F1 c'est quoi ? Une pression ? Une force ? La pression dans le tuyau elle est constante ? Imposée ? La forme du tuyau est imposée donc (et donc sa vitesse aussi, et donc la vitesse de rotation des poulies aussi) ?

[fabang]

Dans ton problème, ce n'est pas la section de la courroie qu'il faudrait changer, mais la longueur.
Sur ton dessin on a l'impression que les poulies ne tournent pas plus que un quart de tour? et pour que les vitesses de rotation des deux poulies soient identique, il faudrait que le diamètre de la courroie augmente de la différence de diamètre qu'il y a entre les deux poulies. En respectant l'échelle des poulies la courroie devient énorme.

[xt63]

Bonjour,

Tout d'abord merci d'essayer de m'aider, c'est sympa.

Obi76: F1 et F2 sont des forces, elles proviennent de la différence de pression entre l'extérieur et l'intérieur du tuyau. La pression dans le tuyau au départ est donnée mais ensuite selon mon fonctionnement comme le volume du tuyau va augmenter la pression va diminuer (un peu). De toute façon pour mon fonctionnement on peut considérer que la vitesse angulaire des deux poulies sont imposées cela ne change rien. En réalité, je partais sur une poulie2 forcée par un moteur, le tuyau est forcé (piloté) aussi et par conséquent la poulie1 est obligée de suivre.

Fabang: Oui effectivement les poulies ne tournent pas plus d'un quart de tour j'ai pas besoin de plus et si je veux plus je pourrai par exemple enrouler le tuyau en forme de spirale sur chaque poulie ça complique juste les calculs. Et oui, le dessin n'est pas à l'échelle (j'ai oublié de mettre les dimensions :/), la poulie1 fait 1000 mm de rayon, la poulie2 fait 500 mm (rayon), le tuyau en sortie de poulie1 fait 2 mm* 2mm de section et le tuyau en arrivant sur la poulie2 fait 6mm*2mm de section. J'aimerai bien ne changer que la longueur mais ce n'est pas possible enfin j'ai trouvé que cette solution pour avoir deux rayons différents et la même vitesse angulaire, si tu connais une autre solution je suis preneur mais j'aimerai aussi savoir si cette solution est correcte en théorie.

Cordialement

[fabang]

Il faudrait que le tuyau atteigne 500mm de diamètre et non pas 6mm pour que les deux poulies aient le même déplacement angulaire.
Ton calcul de surface est étrange et n'a pas de rapport avec le déplacement des poulies.

[xt63]

Re,

La longueur de l'arc (tuyau) sur la poulie1 est de 2Rwt si la poulie1 fait 2R en rayon et la vitesse de rotation est à w.
La longueur de l'arc (tuyau) sur la poulie2 est de Rwt car son rayon est R.

La surface qui vient de la poulie1:

4 surfaces de 2 mm de côté par la longueur de l'arc qui est de 2Rwt soit 16Rwt

La surface qui est sur la poulie2:

2 surfaces de 2 mm côté avec une longueur de Rwt
2 surfaces de X mm de côté avec une longueur de Rwt

soit Rwt(4+2X)

Si on veut la même surface:

Rwt(4+2X)=16Rwt

Donc X=6 mm

Ca me semble possible dans l'ordre de grandeur. La section passe de 4mm^2 à 12 mm^2. Pourquoi pensez vous que le tuyau doit faire 500 mm ?

Cordialement

[fabang]

Malheureusement il n'y a pas de rapport entre le déplacement des poulies et la surface de contact de la courroie.

[xt63]

Les poulies tournent à la vitesse angulaire w (identique pour les deux), elles tournent et la longueur du tuyau qui avance c'est Rwt ou 2Rwt selon la poulie, je parle bien de la surface du tuyau qui glisse les bouts (là où se trouvent F1 et F2) ne changent pas. Je ne comprends pas ce qui ne va pas, et j'aurai besoin d'une explication svp.

J'ai fait les calculs pour un petit bout qui part de la poulie1 et qui va se transformer en petit bout vers la poulie2, je n'ai pas besoin de calculer la longueur totale, juste ce qui change.

Cordialement

[fabang]

J'avoue ne pas comprendre le dessin.
Je suppose que la courroie ne glisse pas sur les poulies?
F1 et F2, ce sont les points d'attache de la courroie sur les poulies?
Peut être que si on avait une idée de l'utilisation, ce serait plus facile à interpréter.
Si tu fais partir 1mm de la poulie 1, ça fait toujours 1mm sur la poulie, même si tu changes le diamètre de la courroie. Ou alors tu penses qu'en gonflant la courroie, elle raccourcie?. Mais dans ce cas elle n'est pas élastique, en quoi donc est fait cette courroie? pourquoi n'y a t'il qu'une partie de la courroie qui gonfle?. Il faudrait que cette courroie soit constituée d'un matériau élastique avec une armature spirale inextensible qui lui permette de raccourcir quand le diamètre augmente.

[xt63]

Effectivement, le tuyau (ou courroie) ne glisse pas sur les poulies. F1 et F2 sont des forces, mais les parois qui donnent naissance aux forces F1 et F2 (différence de pression) sont fixées sur chaque poulie.

L'objectif c'est de vérifier que je peux avoir la même vitesse angulaire avec deux poulies de rayons différents. C'est une question que je me pose, je vais pas faire une machine comme cela.

Oui, je pense qu'en élargissant la section de la poulie, elle avancera moins vite mais il y aura plus de surface là où se trouve la force F2. Je peux imaginer la courroie théoriquement, idéalement elle serait constituée d'une mince paroi et cette paroi serait modifiable sans frottement en pratique il y aura des frottements, mais si la paroi est fine les frottements seront limitées, mais j'essaie déjà de savoir si c'est faisable ou pas du point de vue géométrique déjà. Théoriquement, je pourrai enlever de la matière pour transmettre 100% de l'énergie d'une poulie à l'autre mais je n'en suis pas encore là.

Cordialement

[sitalgo]

B'jour,

Supposons une bouteille fermée dans laquelle règne une faible pression, au hasard 1000 Pa, et posée horizontalement sur une table. Tout cela sous pression atmo à 100 000 Pa.
On peut donc calculer des forces F1 et F2 sur le bouchon et sur le culot, comme tu l'as fait pour ton bazar.
Je voudrais savoir si, à ton avis, la bouteille va se déplacer.

[xt63]

Bonsoir,

La bouteille ne se déplacera pas toute seule. Mais je ne sais pas comment faire l'analogie avec mon exemple car la poulie2 tourne parce qu'elle est forcée de le faire car il y a un moteur qui l'oblige à tourner.

J'ai refait un dessin:



La poulie2 est entraînée par un moteur donc elle va tourner.
Les parois noires possèdent une force (F1 et F2) car il y a une différence de pression. La poulie2 exige de l'énergie de la part du moteur car le couple de la force F2 est horaire et je demande au moteur de faire tourner la poulie dans le sens trigo.
Les parois rouges ne demandent pas d'énergie à déplacer en théorie car la force de pression est perpendiculaire au déplacement et si on regarde l'image montrant 2 positions on voit bien ce qui bouge ou pas, entre autre la partie conique qui agrandit le tuyau ne bouge pas, c'est la paroi qui "glisse" dans l'espace (mais pas de glissement du tuyau sur les poulies).
La poulie1 reçoit un couple provenant de F1 et si le couple résistant n'est pas trop élevé, la poulie1 va tourner (ou continuer de tourner si elle le faisait avant).

Après pour les calculs je ne sais pas, ce n'est peut être pas bon. J'ai fait les calculs en considérant un petit déplacement sur la poulie1 qui doit correspondre à un déplacement sur la poulie2, juste parce que la surface doit être conservée.

Cordialement

[coussin]

Oui donc ce sont des poulies "usuelles" si l'une est entraînée par un moteur et que la courroie ne glisse pas...

[xt63]

Juste une précision: les poulies tournent à la même vitesse angulaire et ça c'est pas possible avec une courroie habituelle, d'où l'utilisation de la différence de pression.

Cordialement

[coussin]

Non, les poulies ne tournent pas à la même vitesse et votre histoire de pression ne tient pas debout. Mais ce n'est que mon avis... Prouvez-moi le contraire.

[fabang]

il y a plein d'incohérences, comme l'application d'une pression aux extrémités d'une courroie mobile ou cette histoire de changement de surface de courroie qui arriverait à modifier la rotation des poulies sans glissement. C'est incompréhensible, il n'y a rien qui tienne dans ces explications.