Bonjour,
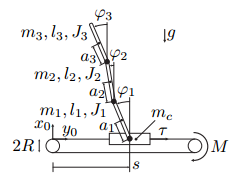
J'essaye de résoudre avec le calcul symbolique de matlab les équations d'euler-lagrange pour le pendule inversé triple.

Nom : PenduleTriple.PNG Affichages : 180 Taille : 14,3 Ko

Mon code est comme ceci

Code:
clear variables
syms a1 real
syms a2 real
syms a3 real
syms l1 real
syms l2 real
syms phi1(t)
syms phi2(t)
syms phi3(t)
syms s(t)
syms u(t)

syms mc real
syms m1 real
syms m2 real
syms m3 real
syms J1 real
syms J2 real
syms J3 real
syms g
syms tau

%damping factors

syms d1 real
syms d2 real
syms d3 real
G=[d1+d2,-d2,0,0;-d2,d2+d3,-d3,0;0,-d3,d3,0;0,0,0,0];
R=0.5*d1*diff(phi1,t)^2+0.5*d2*(diff(phi2,t)-diff(phi1,t))^2+0.5*d3*(diff(phi3,t)-diff(phi2,t))^2;

q=[phi1;phi2;phi3;s];
qdot=diff(q,t);
q=formula(q);
qdot=formula(qdot);

pc0=[s;0]; %position of the cart
pc1=[s-a1*sin(phi1);a1*cos(phi1)];
pc2=[s-l1*sin(phi1)-a2*sin(phi2);l1*cos(phi1)+a2*cos(phi2)];
pc3=[s-l1*sin(phi1)-l2*sin(phi2)-a3*sin(phi3);l1*cos(phi1)+l2*cos(phi2)+a3*cos(phi3)];
yc1=[0,1]*pc1;
yc2=[0,1]*pc2;
yc3=[0,1]*pc3;

vc1=diff(pc1,t);
vc2=diff(pc2,t);
vc3=diff(pc3,t);
vc1Norm2=transpose(vc1)*vc1;
vc1Norm2=simplify(vc1Norm2);
vc2Norm2=transpose(vc2)*vc2;
vc2Norm2=simplify(vc2Norm2);
vc3Norm2=transpose(vc3)*vc3;
vc3Norm2=simplify(vc3Norm2);

V=g*(m1*yc1+m2*yc2+m3*yc3);
gg=[diffDepVar(V,phi1);diffDepVar(V,phi2);diffDepVar(V,phi3);diffDepVar(V,s)];
gg=formula(gg);

T=0.5*(mc*diff(s,t)^2+m1*vc1Norm2+m2*vc2Norm2+m3*vc3Norm2+J1*diff(phi1,t)^2+J2*diff(phi2,t)^t+J3*diff(phi3,t)^2);
T=simplify(T);
L=T-V;
L=simplify(L);

R=0.5*(d1*diff(phi1,t)^2+d2*(diff(phi2,t)-diff(phi1,t))^2+d3*(diff(phi3,t)-diff(phi2,t))^2);
eulerLagrange=@(f,t,x,xd) diff(diffDepVar(f,xd),t)-diffDepVar(f,x)+diffDepVar(R,xd);
dL1=eulerLagrange(L,t,phi1,diff(phi1,t));
eqn1=dL1==0;
dL2=eulerLagrange(L,t,phi2,diff(phi2,t));
eqn2=dL2==0;
dL3=eulerLagrange(L,t,phi3,diff(phi3,t));
eqn3=dL3==0;
dL4=eulerLagrange(L,t,s,diff(s,t));
eqn4=dL4==tau;

dsolve(eqn1,eqn2,eqn3,eqn4);
Mais matlab me dit "explicit solution could not be found". Est-ce qu'il y a une erreur au niveau de la modélisation physique? Au niveau du code?
Merci de votre aide

PS : c1, c2 , c3 sont les centre de masse des barres et R est la fonction de dissipation de Rayleigh (ne pas préter attention à G ou a gg).